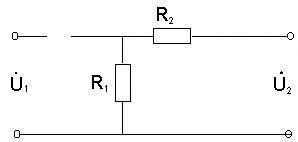
2.5 Активная интегрирующая rc цепь

Активную интегрирующую цепь собирают по схеме, показанной на рисунке 13.

Рисунок 13 – Активная интегрирующая цепь

В данной цепи , т.е. , и, следовательно, цепь является интегрирующей.

2.5 Дифференцирующе–интегрирующая цепь

Цепь, которая состоит из соединенных последовательно дифференцирующей и интегрирующей цепей, называют дифференцирующее–интегрирующей цепью. Воспользуемся рассуждениями, изложенными выше, для дифференцирующей и интегрирующей цепей и получим комплексный коэффициент передачи дифференцирующее–интегрирующей цепи. Если напряжение на конденсаторе равно, то напряжение на резистореравно

Воспользовавшись уравнениями Кирхгофа, выразим через:

Проведем математические преобразования последнего выражения с учетом того, что и:

.

Рисунок 14 – Схема последовательно соединённых дифференцирующей и интегрирующей цепей.

Определим выходное напряжение: или, обозначив граничную частоту, получим окончательно выражение для комплексного коэффициента дифференцирующее–интегрирующей цепи:

.

Найдем модуль коэффициента передачи этой цепи:

.

Проанализируем полученную частотную зависимость:

 при

 при

 при .

При стремлении частоты к нулю или к бесконечности в схеме дифференцирующее–интегрирующей цепи конденсаторы можно заменить разрывом (рисунок 15) и коротким замыканием (рисунок 16), соответственно.

Рисунок 15 – Эквивалентная схема дифференцирующее–интегрирующей цепи при

Рисунок – 16 Эквивалентная схема дифференцирующее–интегрирующей цепи при

График амплитудно-частотной характеристики дифференцирующее–интегрирующей цепи имеет вид размытой резонансной кривой с максимумом на частоте ω₀, называемой квазирезонансной частотой (рисунок 17).

Выразим аргумент комплексного коэффициента дифференцирующее–интегрирующей цепи:

.

Проанализируем полученную частотную зависимость φ(ω):

• при ;

• при ;

• при .

Рисунок 17 – Амплитудно-частотная характеристика дифференцирующее–интегрирующей цепи

Рисунок 18 – Фазочастотная характеристика дифференцирующее–интегрирующей цепи

Результаты анализа позволяют построить фазочастотную характеристику дифференцирующее–интегрирующей цепи (рисунок 18).

3 Метод переходных характеристик Прохождение негармонических сигналов через пасивные и активные rc-цепи

Кроме частного подхода в радиоэлектронике широко используется временной подход. В этом случае электрическая цепь характеризуется переходной функцией или переходной характеристикой. Переходная характеристика – это отклик цепи, то есть – это напряжение на выходе цепи при подаче на её вход единичного скачка напряжения. В хорошо разработанном анализе цепей методом переходных характеристик в качестве элементарного сигнала выбирают мгновенный скачок напряжения, т.е. напряжение, претерпевающее в фиксированный момент времени изменение на некоторую величину , которая может быть принята равной единице. Такой сигнал носит название единичного скачка напряжения. Зависимость от времени выходного напряжения, отнесенного к величине скачка входного напряжения , носит название переходной характеристики цепи. Очевидно, что по самому ее смыслу переходная характеристика определяет искажения сигналов, проходящих через линейные цепи.

При скачке напряжения, приложенного к цепи состоящей из последовательно включенных R и C элементов, в первый момент времени конденсатор C не заряжен и всё напряжение приложено к резистору R. Затем конденсатор начинает заряжаться, а напряжение на резисторе уменьшается. Найдем, по какому закону изменяются напряжения на C и R. Так как токи, протекающие через резистор и конденсатор одинаковые ( I_R=I_C ), то или. Полученное дифферинцеальное уравнение имеет решение:. КонстантаA определяется из начальных условий: при t = 0 U_C = 0. Следовательно, A = -U₁. Тогда Так как входное напряжениеU₂ равно сумме напряжений на конденсаторе и резисторе, то

Таким образом, при подаче на последовательную RC цепь скачка напряжения на конденсаторе напряжение растет, а на резисторе - уменьшается по экспоненциальному закону.