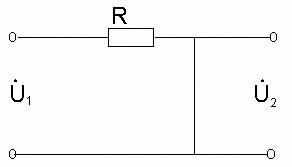
- •Исследование дифференцирующих и интегрирующих цепей
- •1 Rc цепи
- •2 Метод частотных характеристик
- •2.1 Основные понятия
- •2.2 Пассивная дифференцирующая rc цепь.
- •2.3 Активная дифференцирующая rc цепь.
- •2.4 Пассивная интегрирующая rc цепь
- •2.5 Активная интегрирующая rc цепь
- •2.5 Дифференцирующе–интегрирующая цепь
- •3 Метод переходных характеристик Прохождение негармонических сигналов через пасивные и активные rc-цепи
- •3.1 Дифференцирующая цепь
- •Исследование дифференцирующей цепи предварительный расчет
- •Порядок выполнения работы
- •Исследования дифференцирующей цепи методом переходных характеристик
- •Обработка результатов измерений
- •Исследование интегрирующей цепи. Задание
- •Порядок выполнения работы
- •Исследования линейных цепей методом переходных характеристик
- •Вопросы самопроверки для допуска к выполнению лабораторной работы
- •Вопросы самопроверки для защиты лабораторной работы
- •Вопросы самопроверки для допуска к выполнению лабораторной работы
2.3 Активная дифференцирующая rc цепь.
Малый коэффициент
передачи является серьезным недостатком
пассивной дифференцирующей цепи. От
этого недостатка свободна активная
дифференцирующая цепь. Как известно, в
цепи на рисунке 7 а комплексный
коэффициент передачи операционного
усилителя
![]() .
Если в качестве элемента
.
Если в качестве элемента![]() включить
конденсатор емкостью
включить
конденсатор емкостью
![]() ,
а в качестве элемента
,
а в качестве элемента![]() – резистор сопротивлением
– резистор сопротивлением![]() ,
то схема
приобретает вид, показанный на рисунке 7 б.
,
то схема
приобретает вид, показанный на рисунке 7 б.

Рисунок 7 – Активные цепи
Комплексный коэффициент передачи для этого случая имеет вид
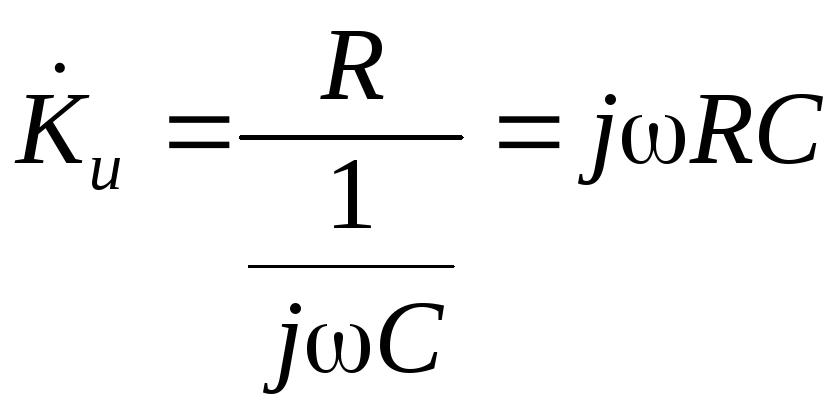 .
.
Но всякая цепь, коэффициент передачи которой пропорционален частоте, представляет дифференцирующую цепь. Если в пассивной дифференцирующей цепи коэффициент передачи много меньше единицы, то в активной цепи он может быть либо близким к единице, либо даже больше единицы при одинаковом качестве дифференцирования.
2.4 Пассивная интегрирующая rc цепь
Интегрирующими называются четырехполюсники, напряжение на выходе которых пропорционально интегралу от напряжения на входе, т.е. четырехполюсники, в которых выполняется условие
![]() .
.
Интегрирующие
цепи могут быть либо пассивными, либо
активными. Покажем, что
цепь на рисунке 8, в которой
![]() является практическиинтегрирующей.
является практическиинтегрирующей.

Рисунок 8 – Схема интегрирующей RC цепи
Если
![]() ,
то
,
то
![]() .В этом случае
.В этом случае
![]() .
Тогда
.
Тогда
![]() .
.
Таким образом,
цепь на рисунке 8
будет практически
интегрирующей, если коэффициент передачи
данной цепи много меньше 1 или постоянная
времени цепи
![]() многобольше
периода входного напряжения
Т.
многобольше
периода входного напряжения
Т.
Проводя для интегрирующей цепи, такие же рассуждения, как и для дифференцирующей цепи, запишем
![]() ,
где
,
где
![]() .
.
Тогда
 ,
,
т.е.
комплексный коэффициент передачи
интегрирующей цепи зависит от частоты![]() .Определим
модуль и аргумент коэффициента
передачи
.Определим
модуль и аргумент коэффициента
передачи
![]() и
и
![]() .
.
Проведём анализ
частотной
зависимости![]() .
.
При стремлении частоты входного сигнала к нулю сопротивление конденсатора стремится к бесконечности, поэтому на месте конденсатора в схеме интегрирующей цепи получается разрыв (рисунок 9);
На высоких частотах, при стремлении частоты входного сигнала к бесконечности, сопротивление конденсатора стремится к нулю и в эквивалентной схеме конденсатор можно заменить коротким замыканием (рисунок 10).
При

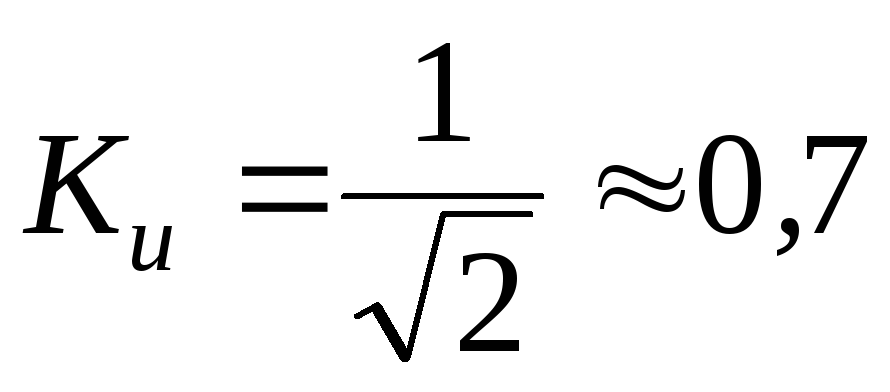 .
.
|
Рисунок
9 – Эквивалентная схема интегрирующей
RC
цепи при
|
Рисунок
10 – Эквивалентная схема интегрирующей
RC
цепи при
|
По
результатам анализа зависимости
![]() интегрирующей
цепи, можно построить амплитудно-частотную
характеристику (рисунок 11).
интегрирующей
цепи, можно построить амплитудно-частотную
характеристику (рисунок 11).
Тангенс
разности фаз между сигналом на выходе
и на входе равен ![]() ,
откуда можно получить фазочастотную
зависимость интегрирующей цепи:
,
откуда можно получить фазочастотную
зависимость интегрирующей цепи:![]() .
Проанализируем эту зависимость:
.
Проанализируем эту зависимость:
При стремлении
 к нулю
к нулю стремится к нулю и
стремится к нулю и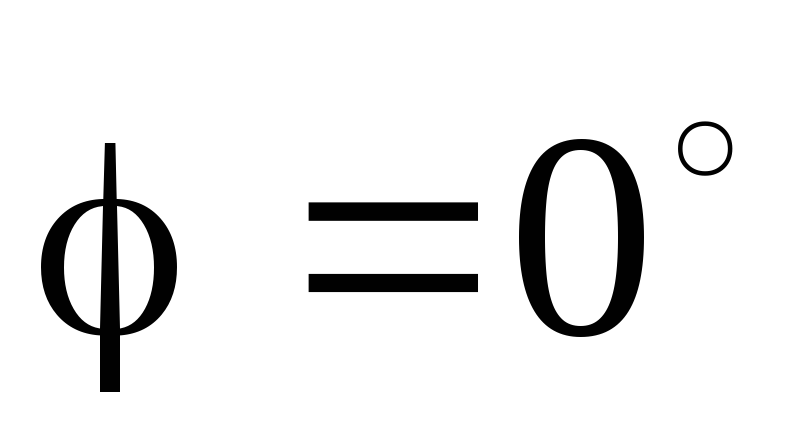
 ,
то есть выходное и входное напряжения
синфазны..
,
то есть выходное и входное напряжения
синфазны..При стремлении
 к бесконечности
к бесконечности стремится к минус бесконечности и
стремится к минус бесконечности и стремится к минус 900,
то есть выходное напряжение отстает
входное на четверть периода.
стремится к минус 900,
то есть выходное напряжение отстает
входное на четверть периода.При
 ,
,
 и
и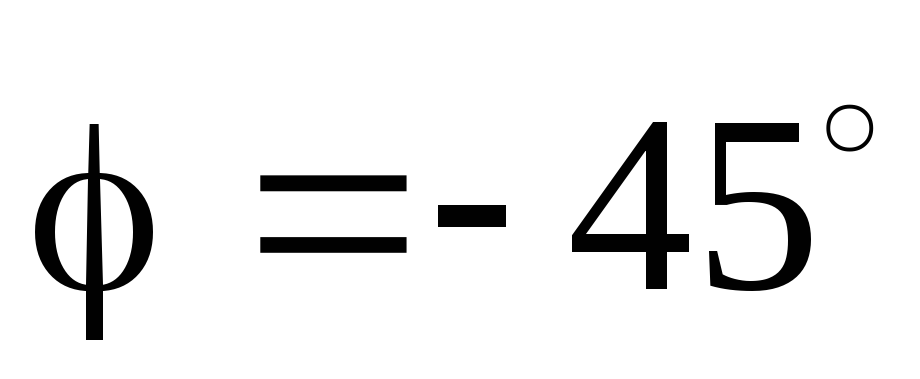 ,
то есть выходное напряжение отстает
входное на восьмую часть периода.
,
то есть выходное напряжение отстает
входное на восьмую часть периода.
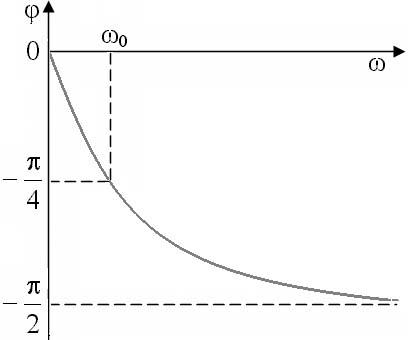
Фазочастотная характеристика данной интегрирующей цепи изображена на рисунок 12.
|
Рисунок 11 – Амплитудно-частотная характеристика интегрирующей цепи |
Рисунок 12 – Фазочастотная характеристика интегрирующей цепи |
Определим условие точного интегрирования гармонического сигнала.
Подадим на вход интегрирующей цепи гармонический сигнал:
![]() ,
,
то выходной сигнал
![]() будет равен
будет равен
![]() ,
,
или
![]() .
.
Обозначим
![]() – амплитуда выходного сигнала. Тогда
– амплитуда выходного сигнала. Тогда
![]() .
.
От сюда видно, что
условием точного интегрирующей сигнала
является отставание выходного сигнала
по фазе на
![]() относительно входного.
относительно входного.
Чтобы выполнялось
условие точного интегрирования сложного
сигнала, необходимо, чтобы для любой
гармоники выходного напряжения отставало
ее входное напряжение на
![]() .
Но
.
Но![]() .
Проводя аналогичные рассуждения как
для точного дифференцирования можно
получить следующее соотношение
.
Проводя аналогичные рассуждения как
для точного дифференцирования можно
получить следующее соотношение![]() т.е. точное интегрирование сигналов
происходит в очень узкой области частот
на высоких частотах, где коэффициент
передачи дифференциальной цепи очень
мал (рисунок 11).
т.е. точное интегрирование сигналов
происходит в очень узкой области частот
на высоких частотах, где коэффициент
передачи дифференциальной цепи очень
мал (рисунок 11).
Таким образом,
интегрирующая
цепь точно
интегрирует
сигналы
только при коэффициенте передачи,
близком к 0. По мере уменьшения величины
![]() C
коэффициент
передачи возрастает, а форма выходного
напряжения
C
коэффициент
передачи возрастает, а форма выходного
напряжения
![]() все больше становится отличной от
значений
все больше становится отличной от
значений![]() ,
все, более приближаясь к форме входного
напряжения
,
все, более приближаясь к форме входного
напряжения![]() .
При
.
При![]() цепь изинтегрирующей
превращается
в разделительную, фаза при этом стремится
к 0 (рисунок 12).
цепь изинтегрирующей
превращается
в разделительную, фаза при этом стремится
к 0 (рисунок 12).
Таким образом,
интегрирующими
являются
цепи, в которых
![]() или
или![]() .
Несмотря на то, что получить идеальное
интегрирования не представляется
возможным,интегрирующие
цепи,
собранные на пассивных
.
Несмотря на то, что получить идеальное
интегрирования не представляется
возможным,интегрирующие
цепи,
собранные на пассивных
![]() -элементах
широко используются на практике.
-элементах
широко используются на практике.
Частотой, при
которой цепь еще не искажает сигнала,
считают граничную частоту цепи равную
![]() .
Оценим диапазон частот, в котором
выполняется условие точного
дифференцирования сигнала.
.
Оценим диапазон частот, в котором
выполняется условие точного
дифференцирования сигнала.