Последовательностъ оценки систематической погрешности
Оценить систематическую погрешность по результатам серии измерений, как это делается для слученной погрешности, невозможно. Кроме того, достаточно часто систематическая погрешность создается несколькими источниками одновременно.
Перед проведением измерений необходимо внимательно проанализировать их методику и оценить максимально возможное влияние различных неучтенных факторов на ожидаемый результат. Это даст оценку сверху величины методической составляющей погрешности.
Затем следует ознакомиться с техническими характеристиками используемых средств измерений и оценить инструментальную погрешность, учитывая все ее составляющие: основную, дополнительную и погрешность, обусловленную взаимодействием средства и объекта измерений.
Как оценить основную инструментальную погрешность
У большинства стрелочных измерительных приборов информация о верхнем пределе их основной инструментальной погрешности содержится в указываемом на шкале прибора его классе точности. Если эта информация по какой - либо причине отсутствует, то инструментальная погрешность принимается равной половине цены деления прибора.
Классом точности прибора называется отношение максимально возможной абсолютной инструментальной погрешности к верхнему пределу измерений прибора (т.е. к показанию прибора при максимальном отклонении стрелки), выраженное в процентах;
(7)
Класс точности измерительного прибора может иметь одно ив восьми значений: 0.06, 0.1, 0.2, 0.6, 1.0, 1.6, 2.6, 4.0.
Зная класс точности прибора, всегда можно оценить его основную инструментальную погрешность. Например, если амперметр может измерять силу тока в диапазоне 0 - 5 А, а его класс точности = 1.5, то
.
Если при измерении силы тока этим прибором зарегистрирована величина 2.55 А, а другие источники погрешности отсутствуют, окончательный результат следует записать в виде: I=(2.55 0.08)А (о правилах округления результата измерений и погрешности см. ниже).
При этом относительная инструментальная погрешность определяется как
(8)
Из соотношения (8) следует, что относительная инструментальная погрешность тем выше, чем на меньший угол отклоняется при измерении стрелка прибора, т.е. чем больше отношение xmax/xизм. В связи с этим многие электроизмерительные приборы выполняются как многопредельные, чтобы обеспечить возможность работы в условиях минимальной относительной погрешности. Для этого рекомендуется выбирать предел измерений таким образом, чтобы показания прибора соответствовали последней трети шкалы.
Иногда из основной инструментальной погрешности выделяют погрешность считывания показаний (погрешность отсчета) и погрешность асимметрии.
Погрешность отсчета вызвана тем, что в процессе считывания экспериментатором показаний стрелочных измерительных приборов имеет место явление параллакса, поскольку стрелка прибора находится на некотором расстоянии от измерительной шкалы (рис.2). В этом случае кажущееся положение стрелки относительно шкалы зависит от угла, под которым экспериментатор смотрит на измерительный прибор.
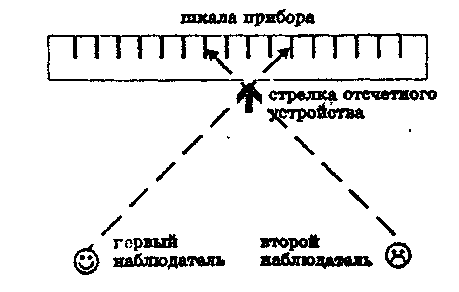
Рис. 2. Зависимость результата отсчета от угла зрения (параллакс)
Для приборов с низкой точностью это явление несущественно, поскольку параллактическая погрешность оказывается намного меньше их основной инструментальной погрешности. У приборов с ≤ 1.5 за измерительной шкалой размещено зеркало. Правильный угол зрения тот, при котором стрелка и ее изображение в зеркале совпадают.
Погрешность асимметрии может возникать при взвешивании тел на рычажных весах (если плечи рычагов неодинаковы), при измерении угла по круговой шкале (если ее центр смещен относительно центра окружности, по которой перемещается визир), при электрических измерениях (если на показания приборов влияет направление протекания тока в электрической цепи). Устранить погрешность асимметрии довольно легко. Например, при взвешивании тел знак погрешности асимметрии зависит от того, на каких чашках весов находятся тело и эталонные гири. Если после взвешивания тело и гири поменять местами, повторить взвешивание еще раз, а затем оба результата сложить и поделить на два, то погрешность асимметрии будет исключена: в одном случае она завышает результат, в другом - занижает. Аналогичным образом следует поступать и в других случаях, когда такая погрешность может появиться.
Если измерения какой-либо величины производятся только одним измерительным прибором, то по характеру проявления его инструментальную погрешность принято считать систематической. Однако, если одна и та же величина измерена несколько раз равными измерительными приборами, то в такой ситуации инструментальная погрешность является случайной: ее величина и знак меняются от прибора к прибору. Усредняя результат таких измерений по формуле (4), можно уменьшить величину инструментальной погрешности, которая в этом случае рассчитывается по формуле (6). Такая процедура "превращения" систематической ошибки в случайную с целью уменьшения погрешности измерений называется рандомизацией (от английского слова random - случайный).
При использовании формул (7), (8) следует помнить, что они определяют не саму основную инструментальную погрешность, а лишь ее максимально возможное значение. Точная величина и знак инструментальной погрешности прибора могут быть найдены только при сопоставлении его показаний с показаниями более точного прибора, измеряющего ту же физическую величину.
Дополнительная
инструментальная погрешность
.
возникает
только при отличии от нормальных условий
применения прибора. Для ее оценки
необходимо изучить техническое описание
используемого прибора.
Формального
правила, позволяющего оценить погрешность,
обусловленную взаимодействием объекта
и средства измерений
не существует.
В каждом конкретном случае при ее оценке анализируют особенности измерительной процедуры и свойства измерительных приборов.
После завершения анализа всех источников результирующая систематическая погрешность находится как сумма модулей методической и всех составляющих инструментальной погрешности.