
- •Тема 01: Принципы компьютерного моделирования химических процессов и их применение в автоматизированных системах.
- •§1. Математическое моделирование.
- •1.1. Принципы системного анализа технологических процессов:
- •1.6. Алгоритм решения системы уравнений мо или моделирующий алгоритм (ма)
- •1.13. Компьютерное моделирование хтп:
- •§3. Системы автоматизированного проектирования, управления и научных исследований сапр (cad) асу (cam) асни (cae)
- •Тема 02. Блочный принцип построения математического описания блочно-структурных физико-химических моделей
- •§1. Общие принципы построения структурной модели
- •§2. Анализ системы уравнений математического описания
- •2.1. Уравнения балансов гидродинамических моделей
- •2.1.1. Уравнения покомпонентного баланса
- •2.1.2. Уравнения общего баланса массы
- •2.1.3. Уравнения теплового баланса
- •2.2. Основные интенсивности источников элементарных процессов в потоках
- •2.3. Условные обозначения в приведённых выше соотношениях:
- •§3. Математическое описание зоны идеального перемешивания (объекта с сосредоточенными параметрами).
- •§4. Математическое описание зоны идеального вытеснения (объекта с распределёнными параметрами).
- •Тема 03. Построение компьютерных моделей теплообменников
- •§1. Построение модели теплообменника типа смешение-смешение
- •1.1. Основные допущения:
- •1.2. Уравнения математического описания:
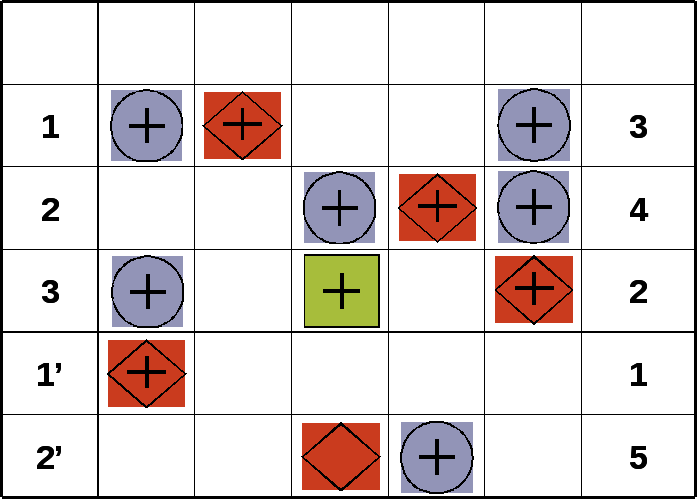
- •1.3. Информационная матрица
- •4.2. Информационная матрица
- •Тема 04: Построение компьютерных моделей гомогенных химических реакторов с мешалкой.
- •§1. Принципы построения компьютерных моделей гомогенных химических реакторов с мешалкой.
- •1.1. Микрокинетика сложной химической реакции
- •1.2. Выбор ключевых компонентов химической реакции.
- •§2. Реактор с мешалкой в стационарном состоянии.
- •3.3. Информационная матрица.
- •1.7. Информационная матрица (противоток)
- •Тема 6 Введение
- •1. Основные допущения:
- •2. Особенности модели:
- •§ 1. Фазовое равновесие жидкость-пар.
- •1.1. Математическое описание процесса для многокомпонентной системы
- •1.2. Информационная матрица системы уравнений математического описания.
- •1.3. Блок-схема алгоритма расчёта.
- •§ 2. Многокомпонентная массопередача на тарелке с учётом гидродинамики движущихся потоков.
- •2.1. Основные допущения:
- •2.2. Математическое описание процесса массопередачи на тарелке.
- •§ 3. Компьютерная модель стационарного режима процесса непрерывной многокомпонентной ректификации в тарельчатой колонне.
- •3.1. Математическое описание процесса
- •3.2. Информационная матрица
- •3.3. Блок – схема алгоритма расчёта стационарного режима тарельчатой ректификационной колонны bp (bubble point) методом
- •3.4. Информационная матрица системы уравнений.
- •§4. Определение составов дистиллята ( ) и кубового продукта ( ) для простой ректификационной колонны с одним конденсатором (дефлегматором) и кипятильником.
- •Тема 07 (часть 1). Построение эмпирических статистических моделей хтп
- •§1. Постановка задачи.
- •§2. Построение эмпирических моделей по данным пассивного эксперимента
- •2.1. Определение вида приближённого уравнения регрессии
- •2.2. Определение коэффициентов регрессии – параметров эмпирических моделей (выполнение первого этапа регрессионного анализа).
- •Тема 07 (часть 2). Построение эмпирических статистических моделей хтп
- •Тема 08. Идентификация математических моделей.
- •§2. Процедура идентификации.
- •§3. Общая стратегия решения задачи идентификации
- •§2. Характеристика оптимизирующих переменных.
- •§3. Численные методы оптимизации.
- •3.1. Экспериментально-статистический метод оптимизации.
- •3.2. Движение к экстремуму методом крутого восхождения.
- •3.3. Уточнение положения экстремума в почти стационарной области.
- •§4. Блок-схема алгоритма экспериментально-статистического метода оптимизации.
4.2. Информационная матрица
Тема 04: Построение компьютерных моделей гомогенных химических реакторов с мешалкой.
§1. Принципы построения компьютерных моделей гомогенных химических реакторов с мешалкой.
МО + МА → ММ
Макрокинетические уравнения – уравнения балансов, записанные с учётом гидродинамической модели движения потока (уравнения покомпонентного баланса, общего баланса массы, энергетический (тепловой) баланс), которые включают в виде слагаемых выражения для интенсивности источников (скоростей) различных «элементарных» процессов, как например, химических превращений, массо- и теплопередачи, фазовых переходов и т.д.
Микрокинетические уравнения – записываются для элементарного объёма, вне зависимости от того, в каком потоке протекает процесс (например, уравнения скорости протекания химических реакций для каждого компонента, уравнения скорости выделения и поглощения тепла за счёт химической реакции). Эти уравнения скоростей называются интенсивностями источников компонентов или локальными интенсивностями источников тепла и включаются в уравнения покомпонентного баланса, уравнение общего баланса массы, а также в уравнения теплового баланса.
1.1. Микрокинетика сложной химической реакции
Скорость химической реакции по каждому компоненту:
n![]() – компонентов, m
–стадий, реакция в жидкой фазе
– компонентов, m
–стадий, реакция в жидкой фазе
Л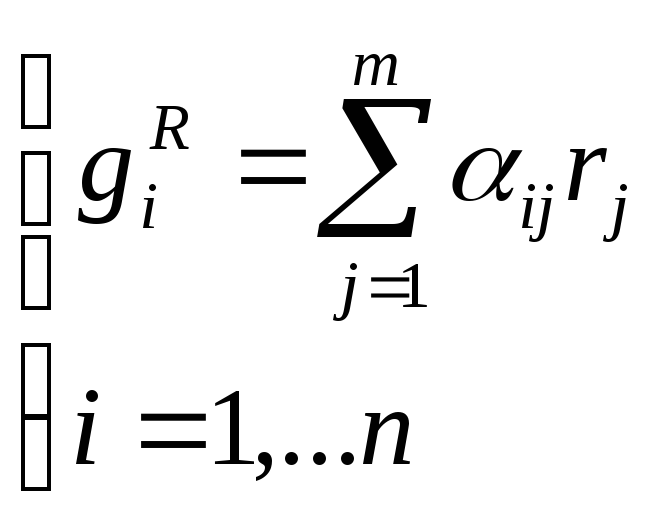 окальная
(отнесённая к единице объёма) скорость
выделения или поглощения тепла в
химической реакции:
окальная
(отнесённая к единице объёма) скорость
выделения или поглощения тепла в
химической реакции:
I )
![]()
rj – скорость j – ой стадии химической реакции, определяемая по закону действующих масс.
αij – стехиометрический коэффициент i – го компонента на j – ой стадии.
αij > 0 i = п - продукт на j – ой стадии;
αij < 0 i = р - реагент на j – ой стадии;
αij = 0 i - отсутствует.
![]() > 0
- компонент
i
образуется;
> 0
- компонент
i
образуется;
![]()
![]() < 0
- компонент
i
расходуется;
< 0
- компонент
i
расходуется;
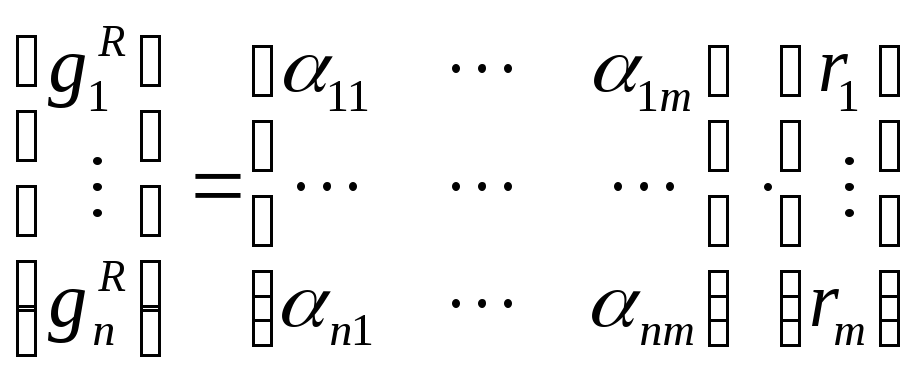
![]()
n = 4, m = 3
![]()
П - произведение
![]() если i
- реагент
если i
- реагент
![]() если i
- продукт или отсутствует
если i
- продукт или отсутствует
( j = 1,…m )
Д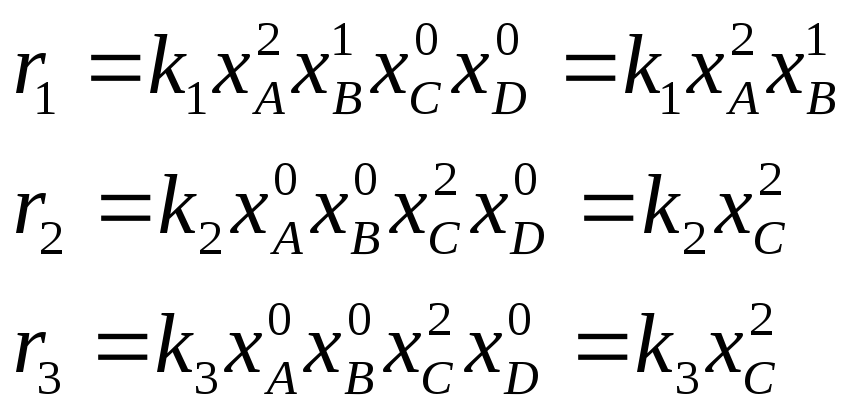 ля
рассматриваемого уравнения реакции:
ля
рассматриваемого уравнения реакции:
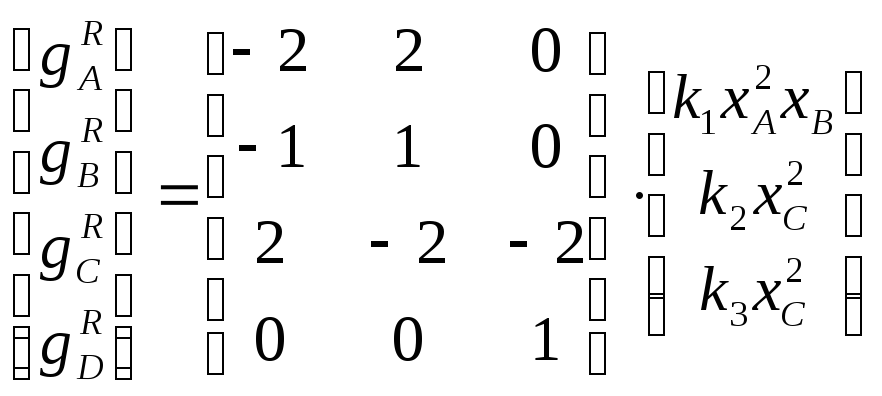
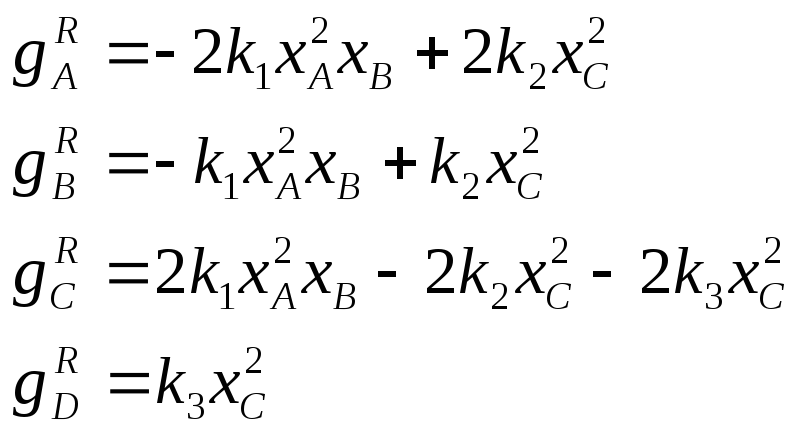
1.2. Выбор ключевых компонентов химической реакции.
Компоненты химической реакции бывают ключевыми и не ключевыми.
Ключевые компоненты – это компоненты, задание которых однозначно характеризует состояние процесса, сопровождаемого химической реакцией, в любой момент времени.
Уравнения МО с учётом гидродинамических условий и микрокинетических закономерностей записываются только для ключевых компонентов, в то время как остальные (не ключевые) компоненты определяются из стехиометрических соотношений.
Процедура выбора ключевых компонентов сложной химической реакции связана с понятием ранга матрицы стехиометрических коэффициентов, который характеризует максимальное число линейно независимых строк или столбцов этой – в общем случае прямоугольной – матрицы.
Д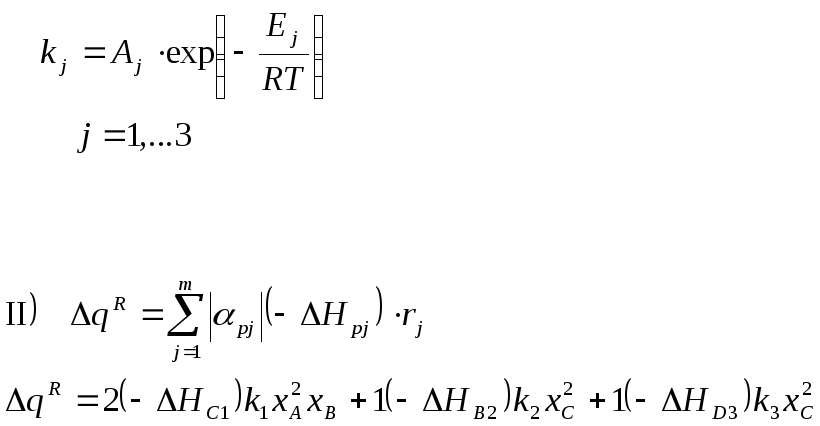 ля
прямоугольной матрицы стехиометрических
коэффициентов размераn
х m
определитель квадратной подматрицы
s-го
порядка называется минором s-го
порядка матрицы стехиометрических
коэффициентов. Рангом матрицы называется
максимальный порядок её минора, отличного
от нуля. Если матрица стехиометрических
коэффициентов имеет минор порядка s,
который отличен от нуля, а любой другой
минор порядка s+1
и выше равен нулю, то ранг матрицы равен
s.
Очевидно, что ранг матрицы может быть
определён как для квадратной, так и для
прямоугольной матриц.
ля
прямоугольной матрицы стехиометрических
коэффициентов размераn
х m
определитель квадратной подматрицы
s-го
порядка называется минором s-го
порядка матрицы стехиометрических
коэффициентов. Рангом матрицы называется
максимальный порядок её минора, отличного
от нуля. Если матрица стехиометрических
коэффициентов имеет минор порядка s,
который отличен от нуля, а любой другой
минор порядка s+1
и выше равен нулю, то ранг матрицы равен
s.
Очевидно, что ранг матрицы может быть
определён как для квадратной, так и для
прямоугольной матриц.
Ранг матрицы стехиометрических коэффициентов равен числу ключевых компонентов химической реакции.
Для математической модели нужна скорость реакции по каждому компоненту. Если удаётся выразить скорости образования одних компонентов через скорости образования других – ключевых компонентов – сокращается количество сложных, в общем случае нелинейных кинетических уравнений, необходимых для описания всего процесса. В результате по концентрациям ключевых компонентов через стехиометрические соотношения можно рассчитать состав всей реагирующей смеси в любой момент времени.
Матрица стехиометрических коэффициентов для рассматриваемого уравнения имеет вид:
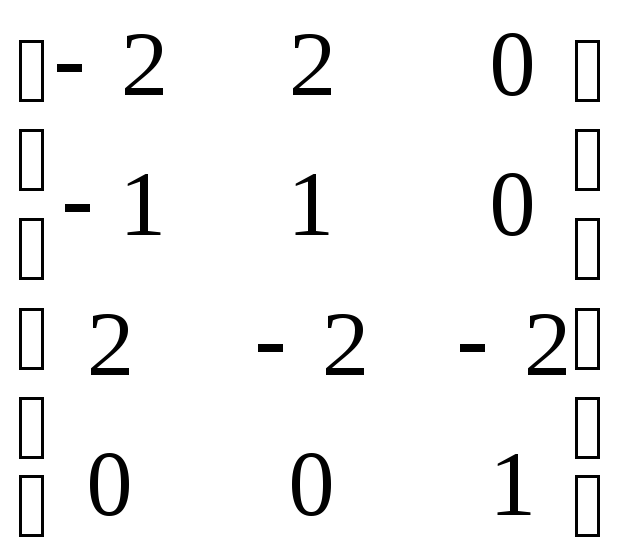
Задача выбора ключевых компонентов реакции сводится к нахождению ранга матрицы стехиометрических коэффициентов. Ранг матрицы, число и наименование ключевых компонентов определяют методами матричного исчисления.
Определим ранг матрицы стехиометрических коэффициентов:
Миноры матриц 3Х3 = 0:

Для матриц 2Х2 есть миноры не равные 0, наивысший порядок минора =2. Ранг матрицы коэффициентов = 2.
Имеем 2 ключевых компонента.
Д![]() ля
скоростей химической реакции по
компонентам будет справедливо:
ля
скоростей химической реакции по
компонентам будет справедливо:
В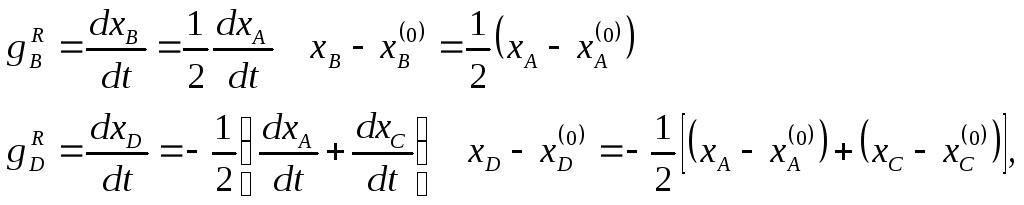 результате в качестве ключевых выбираем
компоненты А и С:
результате в качестве ключевых выбираем
компоненты А и С:
Таким образом, окончательный вид системы уравнений для описания скоростей химической реакции по компонентам включает два кинетических уравнения (вместо первоначальных четырёх) и может быть представлен:
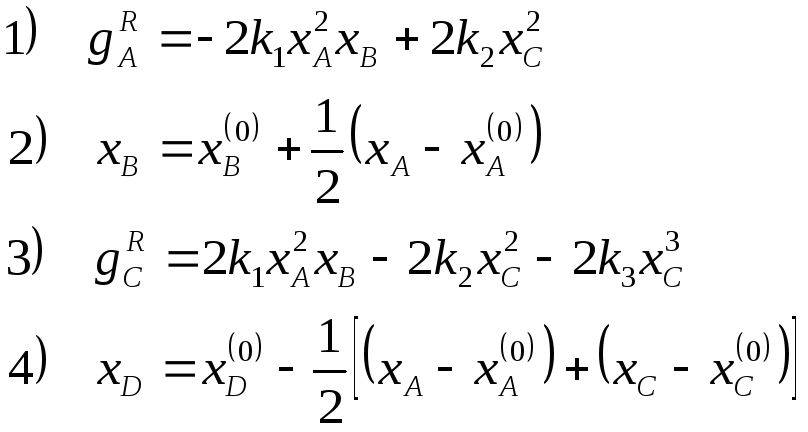
При этом константы скоростей стадий в соответствии с законом Аррениуса выражаются:
![]() - тепловой эффект
j-
стадии, отнесённый к 1 молю продукта р.
- тепловой эффект
j-
стадии, отнесённый к 1 молю продукта р.
