2.3. Условные обозначения в приведённых выше соотношениях:

V - Объём рассматриваемой зоны

v - Расход потока

L - Длина рассматриваемой зоны

D - Коэффициент обратного перемешивания

, T - Состав и температура потока

- Суммарная интенсивность источников тепла в потоке

C_p - Теплоёмкость при постоянном давлении

- Локальные интенсивности источников компонентов в потоке

Δq - Локальная интенсивность источника тепла в потоке

K - Коэффициент передачи, характеризующий интенсивность источников тепла в потоке

ΔН - Тепловой эффект элементарного процесса

- Скорости стадий химической реакции

- Стехиометрические коэффициенты компонентов в реакциях

- Координата пространства

t - Координата времени

n - Число компонентов в многокомпонентной системе

m - Число элементарных стадий в сложной химической реакции

Индексы верхние

⁽⁰⁾ - Признак поступающего в зону потока

^R - Химическая реакция

^M - Массопередача

^A - Изменение агрегатного состояния при фазовом равновесии

^П - Подпитка от «внешнего» потока

^Т - Теплопередача

^И - Теплоизлучение

* - Термодинамическое равновесие

~ - Зона потока, контактирующая с рассматриваемой

Индексы нижние

_i - Компонент - Распределённость параметра

_p - Образующийся компонент (продукт) на элементарной стадии химической реакции.

§3. Математическое описание зоны идеального перемешивания (объекта с сосредоточенными параметрами).

3.1. Описание динамической модели

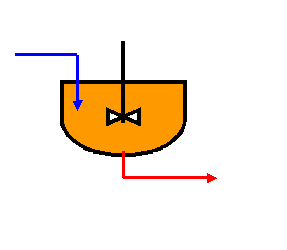
Покомпонентный баланс:

Общий баланс:

Тепловой баланс:

Результат решения:

Для описания нестационарных режимов процессов с сосредоточенными параметрами используется система n+2 обыкновенных дифференциальных уравнений (СОДУ) , 2, 3.

3.2. Описание статической модели

Система конечных уравнений (СКУ)– либо линейных (СЛАУ), либо нелинейных (СНУ).

Для описания стационарных режимов процессов с сосредоточенными параметрами используется система конечных уравнений (СКУ)

Результат конечного решения:

§4. Математическое описание зоны идеального вытеснения (объекта с распределёнными параметрами).

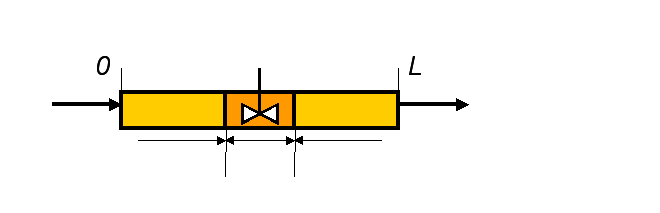
4.1. Описание динамической модели

Покомпонентный баланс – вывод:

где

;

Уравнения покомпонентного баланса:

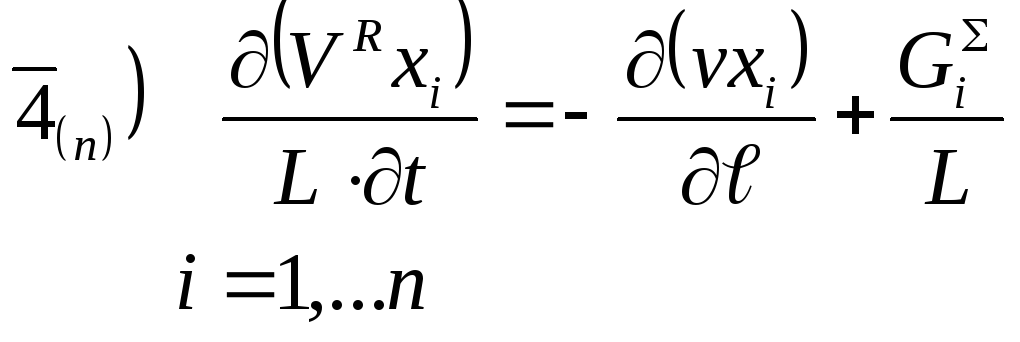
Уравнение общего материального баланса:

Уравнение теплового баланса:

Получили систему n+2 дифференциальных уравнений в частных производных.

Результат решения:

Все переменные зависят от двух независимых координат:

Для описания нестационарных процессов с распределёнными параметрами («труба») используется система дифференциальных уравнений в частных производных (СДУЧП) 4), 5), 6).

4.2. Описание статической модели

Д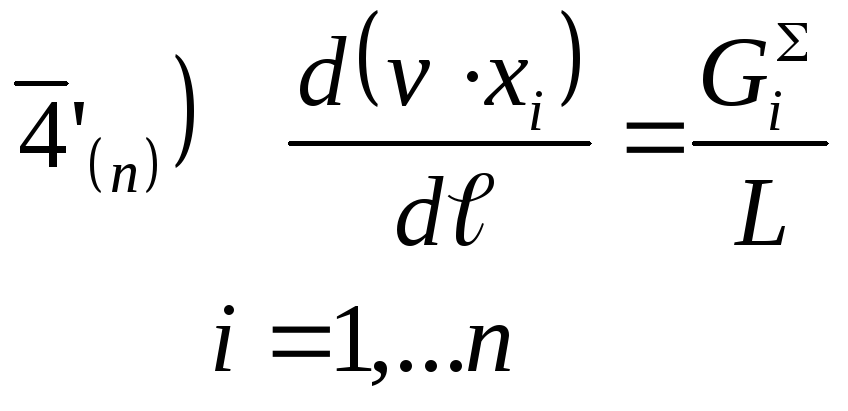ля статической модели все производные по времени равны нулю.

Для описания стационарных режимов процессов с распределёнными параметрами, когда изменение переменных происходит вдоль одной пространственной координаты, используется система обыкновенных дифференциальных уравнений 4’, 5’, 6’:

Решения:

;

Или изменение температуры, концентраций, расходов вдоль длины трубы.

Для того, чтобы моделировать химические процессы, необходимо располагать тремя алгоритмами решения и их комбинациями:

А)систем конечных уравнений (СКУ): систем линейных алгебраических уравнений (СЛАУ) или

Б)систем нелинейных уравнений (СНУ)

систем обыкновенных дифференциальных уравнений (СОДУ)

В)систем дифференциальных уравнений в частных производных (СДУЧП)