§3. Системы автоматизированного проектирования, управления и научных исследований сапр (cad) асу (cam) асни (cae)

 САПР - некоторая система для проектирования, должна включать: hardware - компьютеры, соединённые в ЛВС (LAN), ГВС (WAN) и экспериментальное оборудование software - программное обеспечение orgware - оптимальная организация работы

3.4. АСНИ АСНИ - автоматизированный компьютерный эксперимент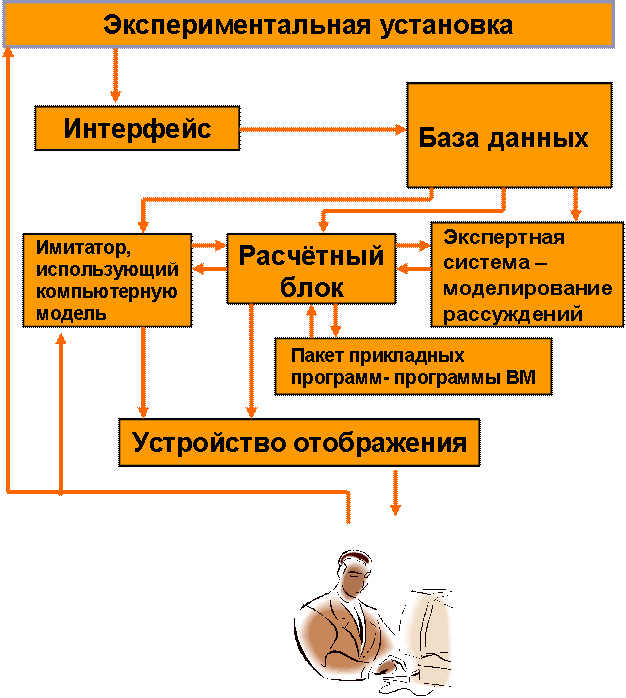

Тема 02. Блочный принцип построения математического описания блочно-структурных физико-химических моделей

§1. Общие принципы построения структурной модели

1. Движущийся поток рассматривается как многофазная, многокомпонентная система (число компонентов = n), для каждой из фаз которой записывают уравнения балансов, базирующиеся на принятой гидродинамической модели движения потока: модель идеального смешения (МИС) и идеального вытеснения (МИВ) – крайние случаи.

2. Реальный поток движущейся фазы может быть представлен в виде комбинированной гидродинамической модели, состоящей из зон ИВ или ИС, причём для каждой зоны записывается своя система уравнений балансов.

3. Для каждой зоны записываются следующие уравнения балансов:

• Уравнение покомпонентных балансов, которое характеризует изменение концентраций компонентов в зоне; число уравнений - n

• Уравнение общего материального баланса, характеризующее изменение расхода потока в зоне; число уравнений -1

• Уравнение теплового баланса, которое характеризует изменение температуры в зоне; число уравнений -1

• Уравнение баланса импульса (количества движения), которое характеризует изменение давления в зоне (в этом курсе не используются).

Балансовых уравнений:

4. Если уравнения балансов включают производные по времени, то строятся динамические математические модели, которые описывают нестационарные режимы движения потока фазы. Если в системе уравнений нет производных по времени, то строятся статические математические модели, которые описывают стационарные режимы движения потока.

5. Основу уравнений математического описания составляют гидродинамические уравнения балансов для движущихся потоков, перечисленные в п.3, в которые включаются интенсивности источников вещества (компонентов) - в уравнения покомпонентных и материального балансов, а также интенсивности источников тепла - в уравнения теплового баланса.

6. Интенсивности источников веществ характеризуют скорости образования или расходования компонентов в потоке за счёт других отличных от гидродинамики элементарных процессов.

7. Интенсивности источников тепла характеризуют скорости выделения или поглощения тепла в потоке за счет также других элементарных процессов.

8. К основным элементарным процессам относятся:

- Химические превращения или реакции

- Массопередача

- Изменение агрегатного состояния или фазовые переходы

- Скорость потока подпитки

-Скорость теплопередачи

- Скорость теплоизлучения

ИТОГО:

i - 1,…n

9. Суммарные источники веществ определяются как аддитивная сумма

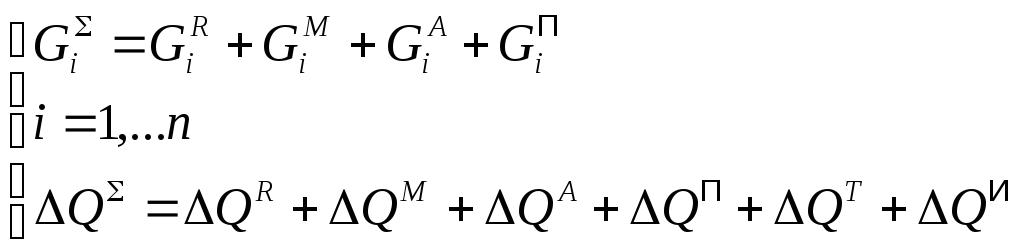
Для совмещённых процессов в этих суммах присутствуют два и более слагаемых, например: хемосорбция – массопередача и химическая реакция.

10. Различают объёмные интенсивности источников элементарных процессов, для локальных интенсивностей которых записываются физико-химические зависимости с соответствующими коэффициентами и поверхностные интенсивности источников элементарных процессов, для которых также записываются физико-химические зависимости с соответствующими

коэффициентами.

Например:

Химическая реакция:

- локальная скорость химической реакции по компоненту i (скорость, отнесённая к единице объёма).

- локальная скорость выделения или поглощения тепла за счёт химической реакции.

Массопередача

- вектор локальных скоростей массопередачи, отнесённых к единице поверхности

- поверхность массопередачи

11. Записываются выражения для локальных интенсивностей элементарных

процессов, зависящие от различных переменных процесса:

Химическая реакция:

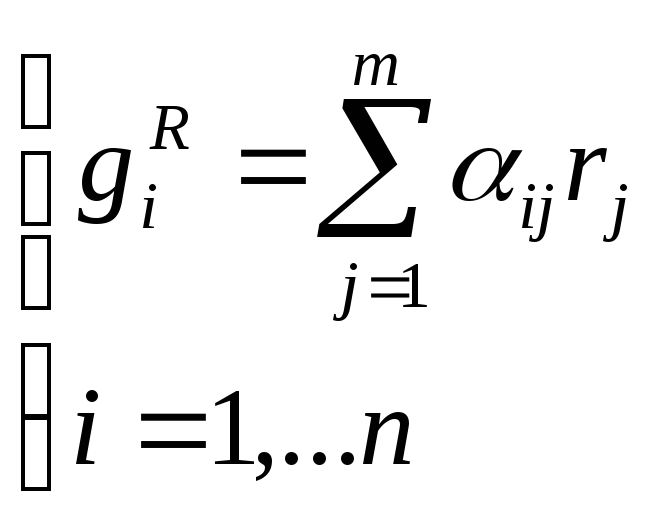
где

П - произведение

если i - реагент

если i - продукт или отсутствует( j = 1,…m )

Массопередача

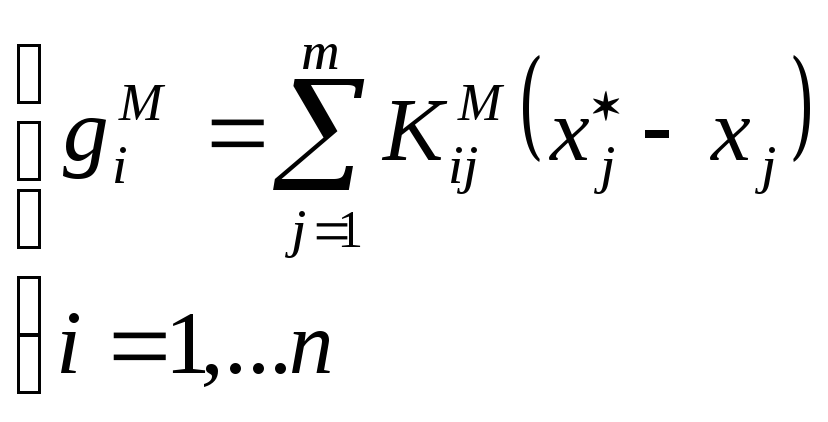
12. Записываются выражения для коэффициентов элементарных процессов, зависящих от различных переменных процесса (коэффициентов теплопередачи К^Т, констант скоростей реакций k_j и т.д.).

13. Записываются уравнения ограничений на конструкционные параметры протекающих процессов, например, длина трубы от 0 до L (где L - длина зоны) и на физические переменные процесса (например, сумма долей компонентов реакции).

В результате получаются уравнения математического описания или система уравнений МО процесса.