Тема 08. Идентификация математических моделей.

Оглавление

§1. Постановка задачи идентификации.

§2. Процедура идентификации.

§3. Общая стратегия решения задачи идентификации

§1. Постановка задачи идентификации.

Идентификация представляет собой основной этап построения адекватной математической модели и сводится к определению конкретного вида функционального оператора Ф (для стационарных моделей) или Ф_t (для динамических моделей):

, где

t - независимая переменная времени

- вектор входных воздействий

- коэффициенты математической модели

Задача идентификации заключается в определении структуры системы уравнений математического описания и значений её коэффициентов, которые обеспечивают наилучшее совпадение выходных переменных модели и процесса при одинаковых входных воздействиях ( ). Процедура идентификации обеспечивает адекватность (соответствие) модели моделируемому объекту.

§2. Процедура идентификации.

Процедура идентификации может быть представлена схематически:

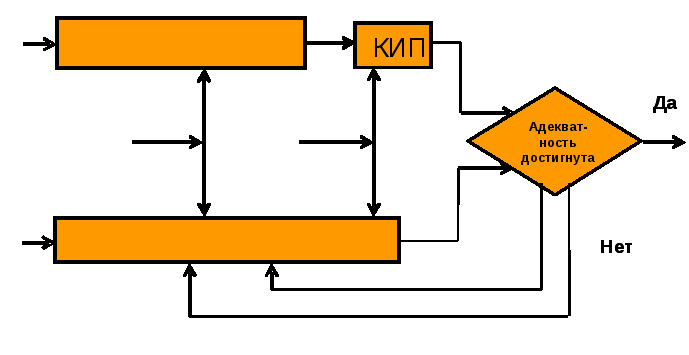
где - вектор выходных переменных

- расчётное значение вектора выходных переменных

- вектор наблюдений выходных переменных с помощью КИП

- шум объекта

- шум приборов

Структурная идентификация математической модели предполагает по данным наблюдения векторов и (если возможно, ) определение структуры уравнений математического описания, т.е. вида и размерности СУМО, а также значений неизвестных коэффициентов .

Как правило, при решении задачи структурной идентификации приходится делать выбор среди конкурирующих моделей с целью определения той из них, которая наиболее точно отражает экспериментальные данные.

Параметрическая идентификация математической модели проводится после того, как форма модели ориентировочно выбрана и имеются в распоряжении данные о переменных на входе и выходе процесса, и заключается в определении неизвестных коэффициентов СУМО.

В случае статической (стационарной) математической модели независимая переменная времени в уравнениях СУМО отсутствует и переменные системы не зависят от t.

Более важным является решение задачи идентификации для динамических (нестационарных) математических моделей, когда они используются при прямом управлении процессами с помощью управляющих компьютеров.

В этом случае необходимо непрерывно в реальном времени с изменением векторов , и выбирать наилучшую модель (структурная идентификация) и оценивать её коэффициенты (параметрическая идентификация), т.е. решать задачу адаптивной идентификации, когда модель непрерывно адаптируется в смысле совпадения расчёта по ней ( ) с данными наблюдений ( ).

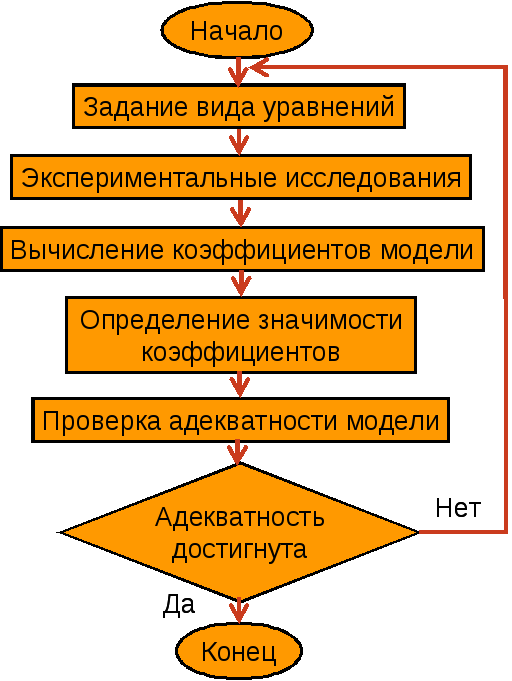
§3. Общая стратегия решения задачи идентификации

Тема 09. Оптимизация математической модели ХТП.

§1. Постановка задачи оптимизации.

§2. Характеристика оптимизирующих переменных.

§3. Численные методы оптимизации.

3.1. Экспериментально-статистический метод оптимизации

3.2. Движение к экстремуму методом крутого восхождения

3.3. Уточнение положения экстремума в почти стационарной области

§4. Блок-схема алгоритма экспериментально-статистического метода оптимизации.

§1. Постановка задачи оптимизации.

Оптимизация – это процедура нахождения наилучших условий проведения химического процесса.

Задача оптимизации рассматривается как математическая задача поиска экстремального значения функции многих переменных.

Формулировка задачи оптимизации для многих переменных:

Необходимо найти такие значения оптимизирующих переменных (ресурсов оптимизации) из допустимой области их определения , которые обеспечивают экстремальную (наибольшую или наименьшую) величину критерия оптимальности.

В результате задачу оптимизации можно представить в следующим виде:

Связь выходных переменных с другими переменными задаётся отображением с физико-химическим оператором:

где входные переменные , определяющие состояние моделируемого объекта, разбиваются на две группы переменных: - оптимизирующие переменные, которые можно контролировать и регулировать и - контролируемые, но не регулируемые переменные (не могут использоваться как ресурсы оптимизации).

В результате задача оптимизации представляется в следующем виде:

На оптимизирующие переменные и выходные переменные могут накладываться ограничения (возможность изменения переменных только в определённых пределах).

На практике выходные переменные при решении задачи оптимизации определяются либо из экспериментальных данных – экспериментально-статистический метод оптимизации, либо с помощью математических моделей процессов – численный метод оптимизации.

Математические модели в этом случае формализуются с помощью отображения с функциональным оператором:

Замена вектора выходных переменных на вектор оценок выходных переменных , полученных при расчёте по математической, модели позволяет рассматривать задачу оптимизации как математическую задачу поиска экстремума функции многих переменных на компьютере.

Задача: определение максимума функции R = R( u )

Результат решения: .

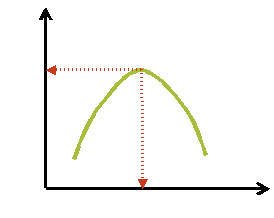
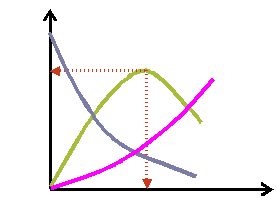
Пример:

Для последовательной реакции A → P → S , изменение концентраций компонентов которой представлено ниже на рисунке, можно сформулировать следующую задачу оптимизации: найти оптимальное время реакции ( t_opt ), при котором концентрация промежуточного продукта Р будет максимальной.

Для решения задачи оптимизации необходимо:

• сформировать критерий оптимальности ( R );

• выбрать оптимизирующие переменные( );

• реализовать конкретный метод определения экстремального значения критерия оптимальности ( численный или экспериментально-статистический ).

Критерий оптимальности является количественной характеристикой качества функционирования процесса.

Различают физико-химические (концентрация целевого продукта, примеси, выход продукта) и экономические (себестоимость, прибыль, рентабельность) критерии оптимальности.

Значение критерия оптимальности зависит от выходной переменной , рассчитываемой с помощью математической модели (численный метод оптимизации). Предполагается, что при оптимизации применяются математические модели, для которых предварительно решена задача идентификации. Соответственно коэффициенты модели не показаны в равенстве:

Если адекватную математическую модель процесса построить не удаётся, то значение выходной переменной в уравнении:

определяется из опытов (экспериментально-статистический метод оптимизации). В этом случае реализуется оптимальная стратегия проведения эксперимента (активный эксперимент).

Требования к критерию оптимальности:

• критерий оптимальности должен быть количественным

• критерий оптимальности должен быть единственным

• критерий оптимальности должен монотонно изменяться в зависимости от оптимизирующих переменных.

Таким образом, при выборе критерия оптимальности необходимо стремиться к тому, чтобы его функция была унимодальной с одним экстремумом и не содержала точек разрыва.