
- •Тема 01: Принципы компьютерного моделирования химических процессов и их применение в автоматизированных системах.
- •§1. Математическое моделирование.
- •1.1. Принципы системного анализа технологических процессов:
- •1.6. Алгоритм решения системы уравнений мо или моделирующий алгоритм (ма)
- •1.13. Компьютерное моделирование хтп:
- •§3. Системы автоматизированного проектирования, управления и научных исследований сапр (cad) асу (cam) асни (cae)
- •Тема 02. Блочный принцип построения математического описания блочно-структурных физико-химических моделей
- •§1. Общие принципы построения структурной модели
- •§2. Анализ системы уравнений математического описания
- •2.1. Уравнения балансов гидродинамических моделей
- •2.1.1. Уравнения покомпонентного баланса
- •2.1.2. Уравнения общего баланса массы
- •2.1.3. Уравнения теплового баланса
- •2.2. Основные интенсивности источников элементарных процессов в потоках
- •2.3. Условные обозначения в приведённых выше соотношениях:
- •§3. Математическое описание зоны идеального перемешивания (объекта с сосредоточенными параметрами).
- •§4. Математическое описание зоны идеального вытеснения (объекта с распределёнными параметрами).
- •Тема 03. Построение компьютерных моделей теплообменников
- •§1. Построение модели теплообменника типа смешение-смешение
- •1.1. Основные допущения:
- •1.2. Уравнения математического описания:
- •1.3. Информационная матрица
- •4.2. Информационная матрица
- •Тема 04: Построение компьютерных моделей гомогенных химических реакторов с мешалкой.
- •§1. Принципы построения компьютерных моделей гомогенных химических реакторов с мешалкой.
- •1.1. Микрокинетика сложной химической реакции
- •1.2. Выбор ключевых компонентов химической реакции.
- •§2. Реактор с мешалкой в стационарном состоянии.
- •3.3. Информационная матрица.
- •1.7. Информационная матрица (противоток)
- •Тема 6 Введение
- •1. Основные допущения:
- •2. Особенности модели:
- •§ 1. Фазовое равновесие жидкость-пар.
- •1.1. Математическое описание процесса для многокомпонентной системы
- •1.2. Информационная матрица системы уравнений математического описания.
- •1.3. Блок-схема алгоритма расчёта.
- •§ 2. Многокомпонентная массопередача на тарелке с учётом гидродинамики движущихся потоков.
- •2.1. Основные допущения:
- •2.2. Математическое описание процесса массопередачи на тарелке.
- •§ 3. Компьютерная модель стационарного режима процесса непрерывной многокомпонентной ректификации в тарельчатой колонне.
- •3.1. Математическое описание процесса
- •3.2. Информационная матрица
- •3.3. Блок – схема алгоритма расчёта стационарного режима тарельчатой ректификационной колонны bp (bubble point) методом
- •3.4. Информационная матрица системы уравнений.
- •§4. Определение составов дистиллята ( ) и кубового продукта ( ) для простой ректификационной колонны с одним конденсатором (дефлегматором) и кипятильником.
- •Тема 07 (часть 1). Построение эмпирических статистических моделей хтп
- •§1. Постановка задачи.
- •§2. Построение эмпирических моделей по данным пассивного эксперимента
- •2.1. Определение вида приближённого уравнения регрессии
- •2.2. Определение коэффициентов регрессии – параметров эмпирических моделей (выполнение первого этапа регрессионного анализа).
- •Тема 07 (часть 2). Построение эмпирических статистических моделей хтп
- •Тема 08. Идентификация математических моделей.
- •§2. Процедура идентификации.
- •§3. Общая стратегия решения задачи идентификации
- •§2. Характеристика оптимизирующих переменных.
- •§3. Численные методы оптимизации.
- •3.1. Экспериментально-статистический метод оптимизации.
- •3.2. Движение к экстремуму методом крутого восхождения.
- •3.3. Уточнение положения экстремума в почти стационарной области.
- •§4. Блок-схема алгоритма экспериментально-статистического метода оптимизации.
§4. Определение составов дистиллята ( ) и кубового продукта ( ) для простой ректификационной колонны с одним конденсатором (дефлегматором) и кипятильником.
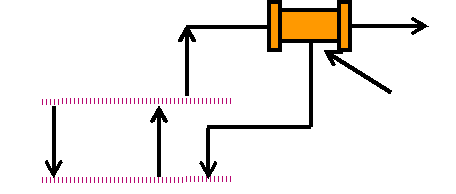
Для конденсатора – дефлегматора (i = 1) при заданном отборе дистиллята D и фазовом равновесии между
жидкостью и паром
в нём (
![]() - константы фазового равновесия жидкость
– пар) будут справедливы следующие
балансовые уравнения:
- константы фазового равновесия жидкость
– пар) будут справедливы следующие
балансовые уравнения:
![]()
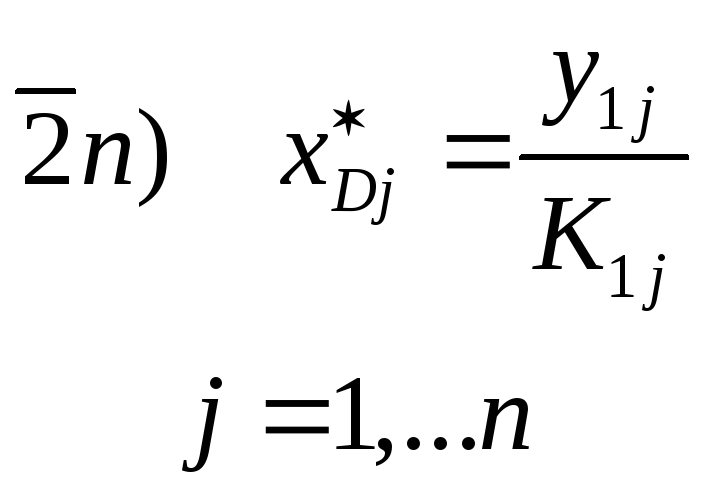
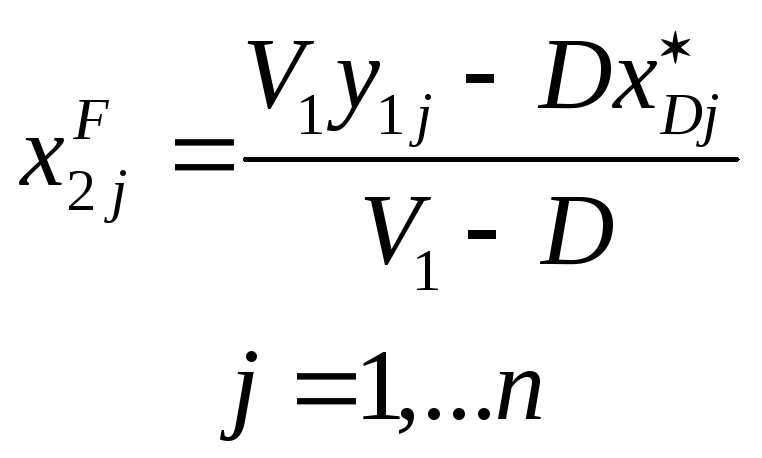
![]()
где
![]() - поток возвращаемой флегмы.
- поток возвращаемой флегмы.
Определяемые величины:
![]()
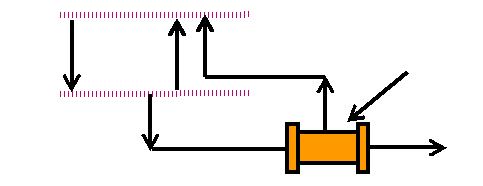
Для кипятильника
(i
= N)
при заданном отборе кубового продукта
W
и фазовом равновесии между жидкостью
и паром в нём (
![]() - константы фазового равновесия жидкость
– пар) будут справедливы следующие
балансовые уравнения:
- константы фазового равновесия жидкость
– пар) будут справедливы следующие
балансовые уравнения:
![]()
![]()
![]()
![]()
где
![]() - поток возвращаемого пара.
- поток возвращаемого пара.
Определяемые величины:
![]()
Тема 07 (часть 1). Построение эмпирических статистических моделей хтп
§1. Постановка задачи.
Эти модели
применяются, когда либо нет информации
о механизме протекающих процессов, либо
они плохо поддаются описанию с
использованием физико-химических
блочных моделей. В этом случае объект
(химико-технологический процесс)
представляется в виде "чёрного ящика"
- кибернетической системы, в которой
единственно доступной информацией
являются её входные
![]() и выходные
и выходные
![]() переменные:
переменные:

где
![]() - вектор входных переменных, влияющих
на состояние системы и её свойства,
- вектор входных переменных, влияющих
на состояние системы и её свойства,
![]() - вектор выходных
переменных, характеризующих состояние
системы.
- вектор выходных
переменных, характеризующих состояние
системы.
В общем случае
строятся эмпирические модели для каждой
отдельной выходной переменной из всех
yi
( i
= 1,…![]() ) в зависимости от всех входных переменных
xi
( i
= 1,…m
), т.е.
) в зависимости от всех входных переменных
xi
( i
= 1,…m
), т.е.
![]()
где
![]() - (m
+ 1) коэффициентов эмпирической модели.
- (m
+ 1) коэффициентов эмпирической модели.
Конкретный вид
функциональной зависимости (f)
и значения коэффициентов
![]() определяются
из опытных данных, т.е. эмпирически.
определяются
из опытных данных, т.е. эмпирически.
Так как результаты опытных измерений являются случайными величинами, то для их обработки используется один из наиболее распространённых методов математической статистики – метод регрессионного и корреляционного анализа.
В соответствии с
методом регрессионного анализа y
считается случайной величиной,
распределённой по нормальному закону
распределения, а компоненты вектора
![]() - детерминированными (неслучайными)
величинами.
- детерминированными (неслучайными)
величинами.
Поэтому согласно
закономерностям теории вероятностей
при каждом фиксированном значении
вектора
![]() величина Y
является случайной величиной с
определённым (зависящим от
величина Y
является случайной величиной с
определённым (зависящим от
![]() )
условным распределением вероятностей.
)
условным распределением вероятностей.
В связи с этим для
нормального закона распределения Y
(допущение регрессионного анализа) для
описания функции (1) используется
зависимость условного математического
ожидания
![]() от
от
![]() ,
которая называется уравнением регрессии:
,
которая называется уравнением регрессии:
![]()
Коэффициенты
уравнения
![]() называются теоретическими коэффициентами
регрессии.
называются теоретическими коэффициентами
регрессии.
Так как коэффициенты
определяются по ограниченной выборке
экспериментальных данных, то их значения
отличаются от истинных (теоретических)
![]() и обозначаются
и обозначаются
![]() (выборочные коэффициенты регрессии). В
результате пользуются приближённым
уравнением регрессии, в котором вместо
условного математического ожидания
(выборочные коэффициенты регрессии). В
результате пользуются приближённым
уравнением регрессии, в котором вместо
условного математического ожидания
![]() фигурирует оценка
фигурирует оценка
![]() и выборочные коэффициенты регрессии
и выборочные коэффициенты регрессии
![]() :
:
![]()
Для приближённого уравнения регрессии эмпирической статистической модели на выборке экспериментальных данных необходимо решить три основные задачи:
А)определить конкретный вид функции (3), т.е. решить задачу структурной идентификации;
Б)определить
выборочные (эмпирические) коэффициенты
регрессии
![]() ,
т.е. решить задачу параметрической
идентификации;
,
т.е. решить задачу параметрической
идентификации;
В)провести статистический (регрессионный) анализ полученных результатов с целью оценки погрешностей полученной модели.
