- •Тема 01: Принципы компьютерного моделирования химических процессов и их применение в автоматизированных системах.
- •§1. Математическое моделирование.
- •1.1. Принципы системного анализа технологических процессов:
- •1.6. Алгоритм решения системы уравнений мо или моделирующий алгоритм (ма)
- •1.13. Компьютерное моделирование хтп:
- •§3. Системы автоматизированного проектирования, управления и научных исследований сапр (cad) асу (cam) асни (cae)
- •Тема 02. Блочный принцип построения математического описания блочно-структурных физико-химических моделей
- •§1. Общие принципы построения структурной модели
- •§2. Анализ системы уравнений математического описания
- •2.1. Уравнения балансов гидродинамических моделей
- •2.1.1. Уравнения покомпонентного баланса
- •2.1.2. Уравнения общего баланса массы
- •2.1.3. Уравнения теплового баланса
- •2.2. Основные интенсивности источников элементарных процессов в потоках
- •2.3. Условные обозначения в приведённых выше соотношениях:
- •§3. Математическое описание зоны идеального перемешивания (объекта с сосредоточенными параметрами).
- •§4. Математическое описание зоны идеального вытеснения (объекта с распределёнными параметрами).
- •Тема 03. Построение компьютерных моделей теплообменников
- •§1. Построение модели теплообменника типа смешение-смешение
- •1.1. Основные допущения:
- •1.2. Уравнения математического описания:
- •1.3. Информационная матрица
- •4.2. Информационная матрица
- •Тема 04: Построение компьютерных моделей гомогенных химических реакторов с мешалкой.
- •§1. Принципы построения компьютерных моделей гомогенных химических реакторов с мешалкой.
- •1.1. Микрокинетика сложной химической реакции
- •1.2. Выбор ключевых компонентов химической реакции.
- •§2. Реактор с мешалкой в стационарном состоянии.
- •3.3. Информационная матрица.
- •1.7. Информационная матрица (противоток)
- •Тема 6 Введение
- •1. Основные допущения:
- •2. Особенности модели:
- •§ 1. Фазовое равновесие жидкость-пар.
- •1.1. Математическое описание процесса для многокомпонентной системы
- •1.2. Информационная матрица системы уравнений математического описания.
- •1.3. Блок-схема алгоритма расчёта.
- •§ 2. Многокомпонентная массопередача на тарелке с учётом гидродинамики движущихся потоков.
- •2.1. Основные допущения:
- •2.2. Математическое описание процесса массопередачи на тарелке.
- •§ 3. Компьютерная модель стационарного режима процесса непрерывной многокомпонентной ректификации в тарельчатой колонне.
- •3.1. Математическое описание процесса
- •3.2. Информационная матрица
- •3.3. Блок – схема алгоритма расчёта стационарного режима тарельчатой ректификационной колонны bp (bubble point) методом
- •3.4. Информационная матрица системы уравнений.
- •§4. Определение составов дистиллята ( ) и кубового продукта ( ) для простой ректификационной колонны с одним конденсатором (дефлегматором) и кипятильником.
- •Тема 07 (часть 1). Построение эмпирических статистических моделей хтп
- •§1. Постановка задачи.
- •§2. Построение эмпирических моделей по данным пассивного эксперимента
- •2.1. Определение вида приближённого уравнения регрессии
- •2.2. Определение коэффициентов регрессии – параметров эмпирических моделей (выполнение первого этапа регрессионного анализа).
- •Тема 07 (часть 2). Построение эмпирических статистических моделей хтп
- •Тема 08. Идентификация математических моделей.
- •§2. Процедура идентификации.
- •§3. Общая стратегия решения задачи идентификации
- •§2. Характеристика оптимизирующих переменных.
- •§3. Численные методы оптимизации.
- •3.1. Экспериментально-статистический метод оптимизации.
- •3.2. Движение к экстремуму методом крутого восхождения.
- •3.3. Уточнение положения экстремума в почти стационарной области.
- •§4. Блок-схема алгоритма экспериментально-статистического метода оптимизации.
§ 3. Компьютерная модель стационарного режима процесса непрерывной многокомпонентной ректификации в тарельчатой колонне.
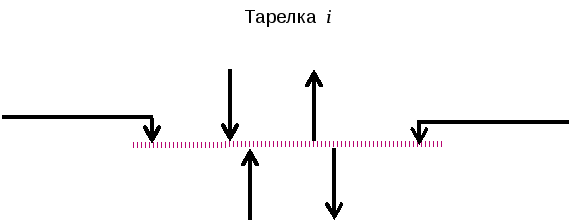
![]() - внешние потоки
тепла (в конденсаторе «минус», в
кипятильнике «плюс»)
- внешние потоки
тепла (в конденсаторе «минус», в
кипятильнике «плюс»)
![]() - энтальпии паровой
(жидкой) фаз;
- энтальпии паровой
(жидкой) фаз;
Fi - внешний поток жидкого питания;
N - число тарелок;
i - номер тарелки ( i = 1,…n );
j - номер компонента ( j = 1,…n ).
При составлении
МО процесса уравнения
![]() для тарелок надо повторить N
раз (первый индекс i
меняется от
1 до N
), добавить
для всех тарелок уравнения теплового
баланса и стехиометрические соотношения
для состава паровой и жидкой фаз.
для тарелок надо повторить N
раз (первый индекс i
меняется от
1 до N
), добавить
для всех тарелок уравнения теплового
баланса и стехиометрические соотношения
для состава паровой и жидкой фаз.
В результате получается МО стационарного режима процесса непрерывной ректификации.
3.1. Математическое описание процесса
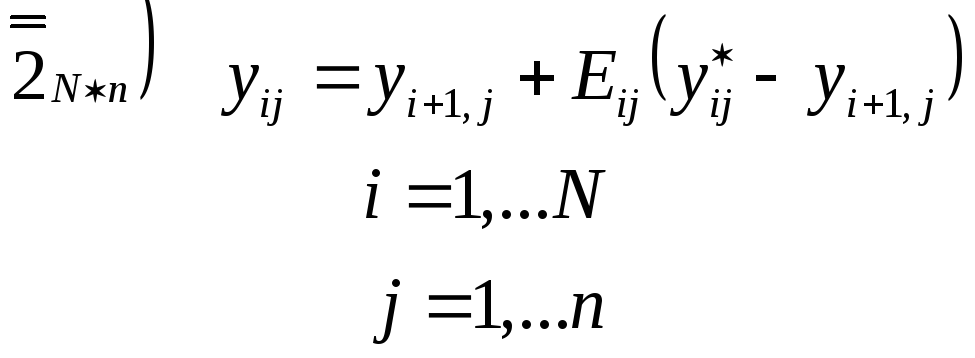
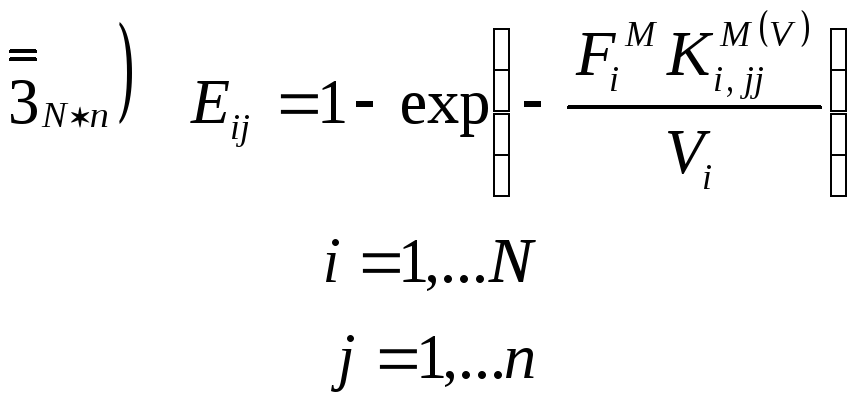
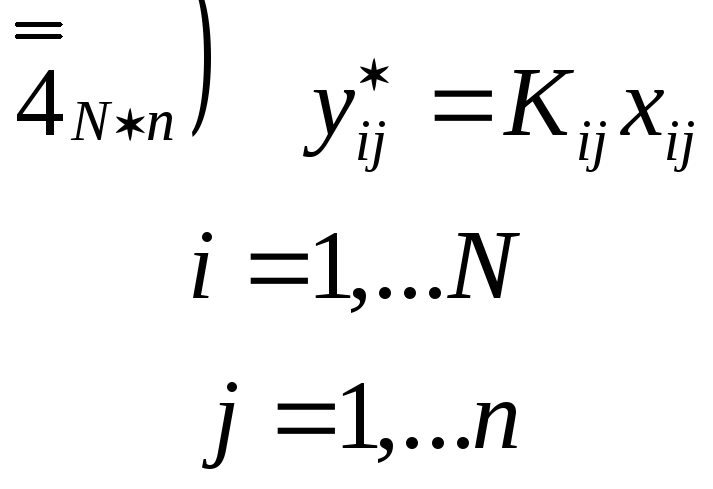
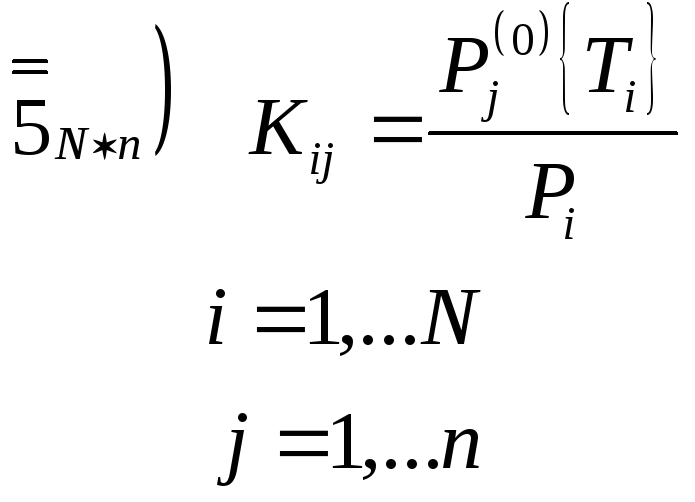
![]()
Стехиометрические соотношения:
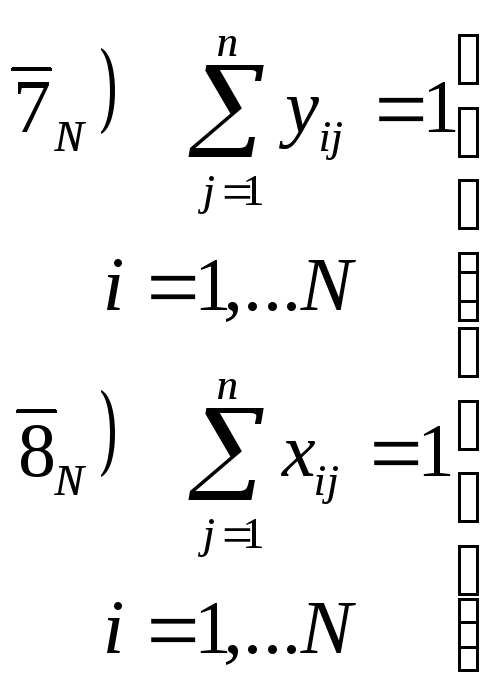
![]()
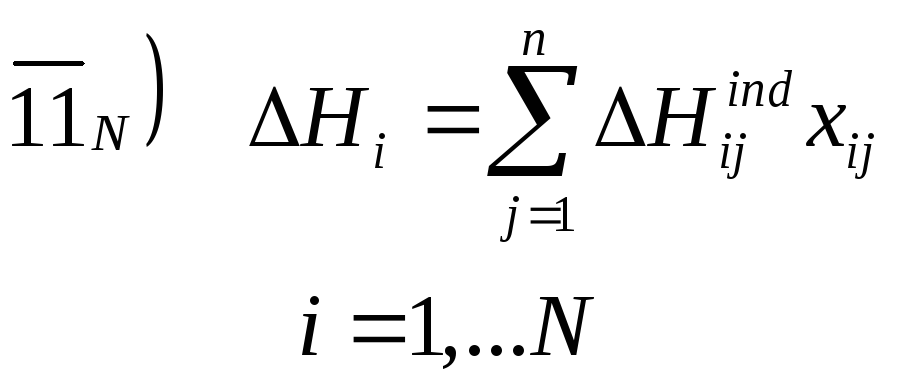
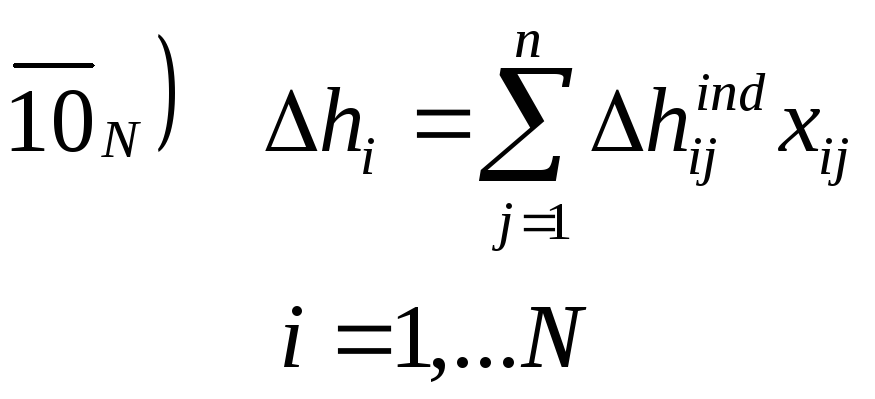
![]()
![]()
![]() - известные
константы для жидкой и паровой фаз.
- известные
константы для жидкой и паровой фаз.
Для удобства
расчётов необходимо сложить уравнения
![]() с учётом стехиометрических соотношений
с учётом стехиометрических соотношений
![]() и
и
![]() ,
в результате чего получаем уравнение
баланса потоков на каждой тарелке
,
в результате чего получаем уравнение
баланса потоков на каждой тарелке
![]() ,
а соотношения
,
а соотношения
![]() исключаем из системы:
исключаем из системы:
![]()
В результате получается система 8 N*n + 5 N независимых уравнений:
- 8 N*n
уравнений:
![]()
- 5 N
уравнений:
![]()
и в качестве определяемых переменных выбираются также 8 N*n + 5 N переменных:
![]()
т.е. получена система нелинейных уравнений (СНУ), для решения которой методом математической декомпозиции можно использовать приведенную ниже информационную матрицу.
3.2. Информационная матрица
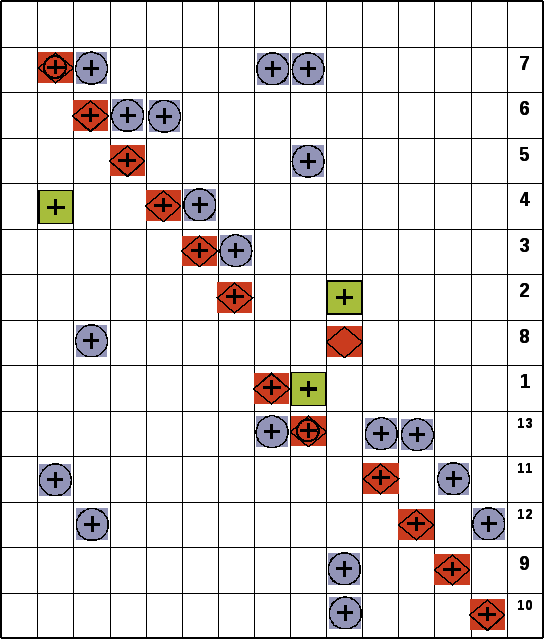
3.3. Блок – схема алгоритма расчёта стационарного режима тарельчатой ректификационной колонны bp (bubble point) методом
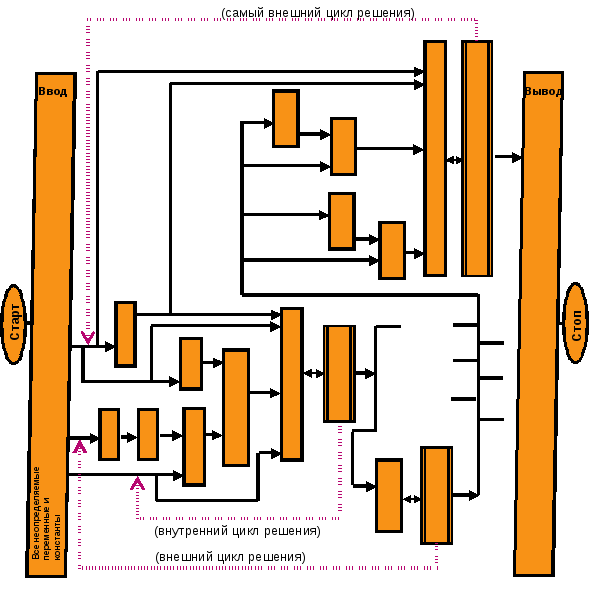
Во внутреннем
итерационном цикле
решается СНУ
![]() относительно
относительно
![]() :
:
![]()
Для теоретической тарелки, когда Eij = 1 , представленное уравнение может быть записано:
![]()
или
![]()
Это уравнение можно записать n раз относительно концентрации каждого компонента (например, компонента j ):
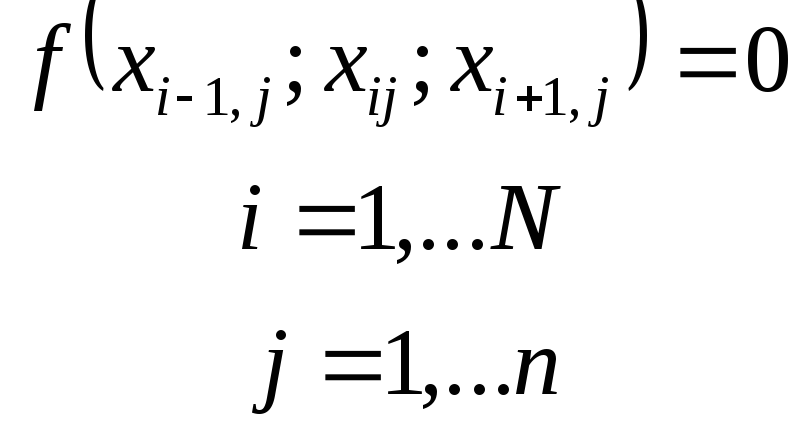
или ( для компонента j ):
![]()
![]()
Последняя система уравнений решается n раз для каждого компонента, для чего используется метод решения трёхдиагональных систем уравнений.
![]()
![]()
3.4. Информационная матрица системы уравнений.
При решении
корректирующее уравнение относительно
![]() :
:
![]()
определяется распределение произвольного компонента (например, j) по высоте колонны:
![]()
Для всех компонентов при n - кратном решении получается искомая матрица:

После этого производится нормировка состава жидкой фазы на каждой тарелке:
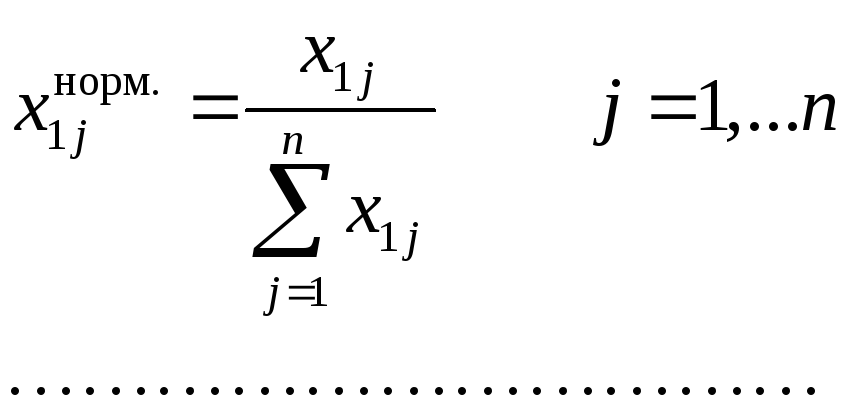
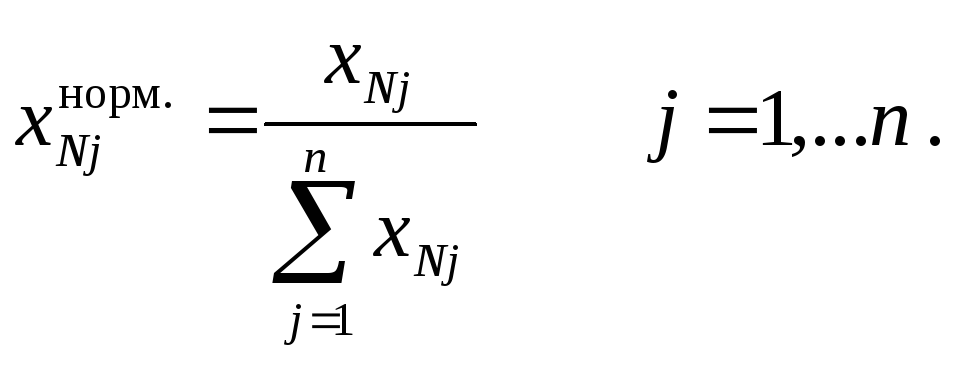
Полученные нормированные значения используются для дальнейших расчётов (см. блок-схему алгоритма расчёта).
Если при
парожидкостном равновесии жидкая фаза
неидеальна и константа равновесия
зависит от состава жидкой фазы, то
решение системы уравнений
![]() рассмотренным методом повторяется до
тех пор, пока нормированные значения
рассмотренным методом повторяется до
тех пор, пока нормированные значения
![]()
на двух последующих итерациях не совпадут.
Во внешнем
итерационном цикле
решается система нелинейных уравнений
![]() относительно
относительно
![]() :
:
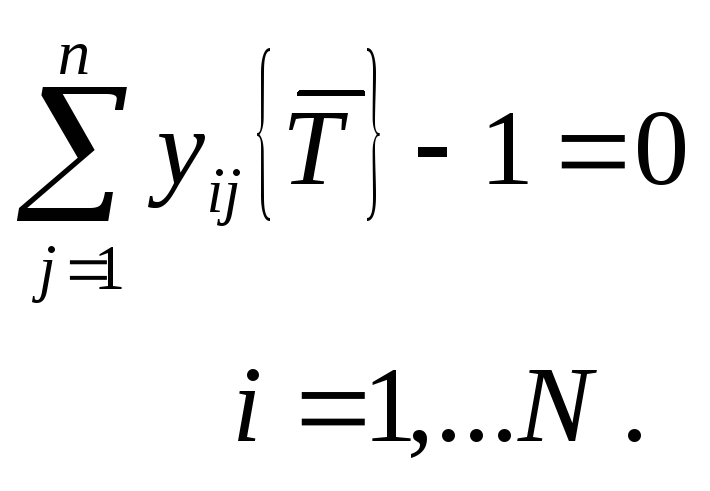
В самом
внешнем итерационном цикле
решается система нелинейных уравнений
![]() относительно
относительно
![]() :
:
![]()
В результате схема итерационных циклов решения BP (bubble point) методом имеет вид: