
Физика1
.doc
1. Точка движется
по окружности радиусом
![]() Закон её движения выражается уравнением
Закон её движения выражается уравнением
![]() где
где
![]() Определить момент времени
Определить момент времени
![]() ,
когда нормальное ускорение
,
когда нормальное ускорение
![]() точки равно
точки равно
![]() Найти скорость
Найти скорость
![]() ,
тангенциальное
,
тангенциальное
![]() и полное
и полное
![]() ускорения точки в тот же момент времени
ускорения точки в тот же момент времени
![]() .
.
Решение.
Найдем скорость точки как производную пути:
![]() м\с.
м\с.
нормальное ускорение
равно
![]() .
Отсюда искомый момент времени
.
Отсюда искомый момент времени
![]() .
.
Найдем
![]() с.
с.
В этот момент
времени скорость равна
![]() м\с.
м\с.
Тангенциальное
ускорение равно по определению
![]() м\с2 и постоянно.
м\с2 и постоянно.
Полное ускорение найдем как
![]() ,
получим
,
получим
![]() м\с2.
м\с2.
Ответ: t=1.5
с,
![]() м\с,
м\с,
![]() м\с2,
м\с2,
![]() м\с2.
м\с2.
2. Шар массой
![]() сталкивается с шаром массой
сталкивается с шаром массой
![]() Скорость первого шара
Скорость первого шара
![]() второго -
второго -
![]() Найти общую скорость
Найти общую скорость
![]() шаров после удара в двух случаях: 1) малый
шар нагоняет большой шар, движущийся в
том же направлении; 2) шары движутся
навстречу друг другу. Удар считать
прямым, центральным, неупругим.
шаров после удара в двух случаях: 1) малый
шар нагоняет большой шар, движущийся в
том же направлении; 2) шары движутся
навстречу друг другу. Удар считать
прямым, центральным, неупругим.
Решение.
При неупругом ударе после столкновения шары движутся как одно целое.
Поэтому по закону сохранения импульса:
в первом случае
![]() ,
откуда
,
откуда
 .
.
Во втором случае
![]() ,
откуда
,
откуда
 .
.
Найдем
1)
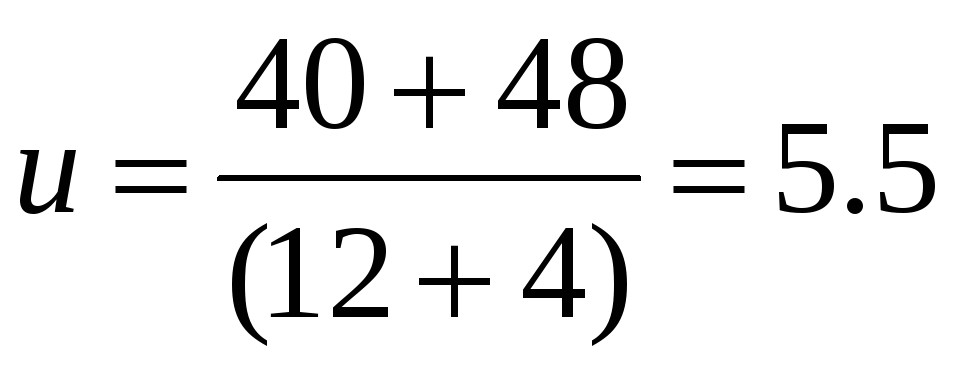 м\с,
м\с,
2)
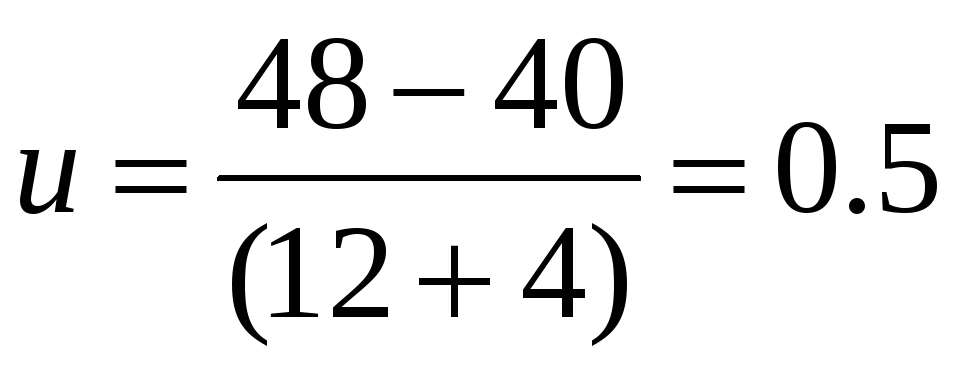 м\с.
м\с.
Ответ: 1) 5.5 м\с, 2) 0.5 м\с.
3. В деревянный шар
массой
![]() подвешенный на нити длиной
подвешенный на нити длиной
![]() попадает горизонтально летящая пуля
массой
попадает горизонтально летящая пуля
массой
![]() С какой скоростью летела пуля, если нить
с шаром и застрявшей в нем пулей
отклонилась от вертикали на угол
С какой скоростью летела пуля, если нить
с шаром и застрявшей в нем пулей
отклонилась от вертикали на угол
![]() ?
Размером шара пренебречь. Удар пули
считать прямым, центральным.
?
Размером шара пренебречь. Удар пули
считать прямым, центральным.
Решение.
При ударе по закону
сохранения импульса
![]() (пренебрегая массой пули).
(пренебрегая массой пули).
После удара по
закону сохранения энергии
![]() .
.
Скорость шара
отсюда равна
![]() .
.
Тогда для скорости пули получим
 .
.
Найдем
![]() м\с.
м\с.
Ответ: 440 м\с.
4. Платформа в виде
диска вращается по инерции около
вертикальной оси с частотой
![]() На краю платформы стоит человек. Когда
человек перешёл в центр платформы,
частота возросла до
На краю платформы стоит человек. Когда
человек перешёл в центр платформы,
частота возросла до
![]() Масса человека
Масса человека
![]() Определить массу платформы. Момент
инерции человека рассчитывать как для
материальной точки.
Определить массу платформы. Момент
инерции человека рассчитывать как для
материальной точки.
Решение.
По закону сохранения
момента импульса
![]() получим
получим
![]() .
.
Угловая частота
связана с линейной как
![]() ,
момент инерции платформы с человеком
на краю равен
,
момент инерции платформы с человеком
на краю равен
![]() ,
а с человеком в центре
,
а с человеком в центре
![]() .
.
Получаем
![]() ,
откуда
,
откуда
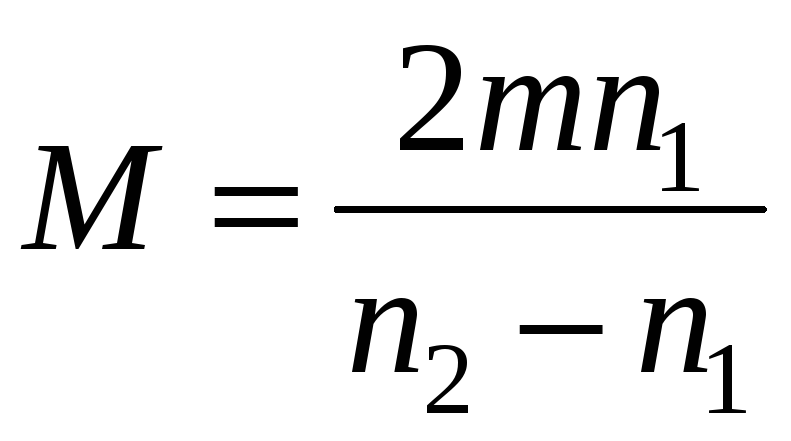 .
.
Найдем
![]() кг.
кг.
Ответ: 178 кг.
5. Какая работа
![]() будет совершена силами гравитационного
поля при падении на Землю тела массой
будет совершена силами гравитационного
поля при падении на Землю тела массой
![]() :
1) с высоты
:
1) с высоты
![]() ;
2) из бесконечности?
;
2) из бесконечности?
Решение.
На тело действует
сила тяготения, равная
![]() .
.
При изменении высоты работа этой силы будет даваться интегралом

Для падения из бесконечности получим
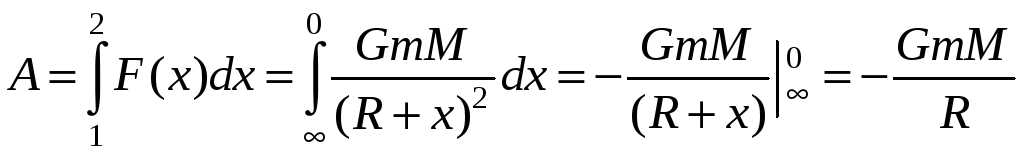
Вычисление даст А1=-16.9 МДж, А2=-125 МДж.
Ответ: 1) А=-16.9 МДж, 2) А-125 МДж.
6. Плотность газа
![]() при давлении
при давлении
![]() и температуре
и температуре
![]() равна
равна
![]() Найти молярную массу
Найти молярную массу
![]() газа.
газа.
Решение.
Из уравнения
состояния газа
![]() выразим молярную массу как:
выразим молярную массу как:
![]() .
.
Найдем
![]() кг\моль.
кг\моль.
Ответ: 0.032 кг\моль.
7. В баллоне
вместимостью
![]() находится смесь, содержащая
находится смесь, содержащая
![]() водорода,
водорода,
![]() водяного пара и
водяного пара и
![]() оксида углерода. Температура смеси
оксида углерода. Температура смеси
![]() Определить давление.
Определить давление.
Решение.
По закону Дальтона
давление смеси газов равно сумме
парциальных давлений составляющих,
![]() .
.
Для каждого газа
из уравнения состояния давление равно
![]() ,
поэтому в сумме получим
,
поэтому в сумме получим
 .
.
Найдем
 Па=1.56 МПа.
Па=1.56 МПа.
Ответ: 1.56 МПа.
8. Определить
среднюю квадратичную скорость
![]() молекулы газа, заключенного в сосуд
вместимостью
молекулы газа, заключенного в сосуд
вместимостью
![]() под давлением
под давлением
![]() Масса газа
Масса газа
![]()
Решение.
Средняя квадратичная скорость равна
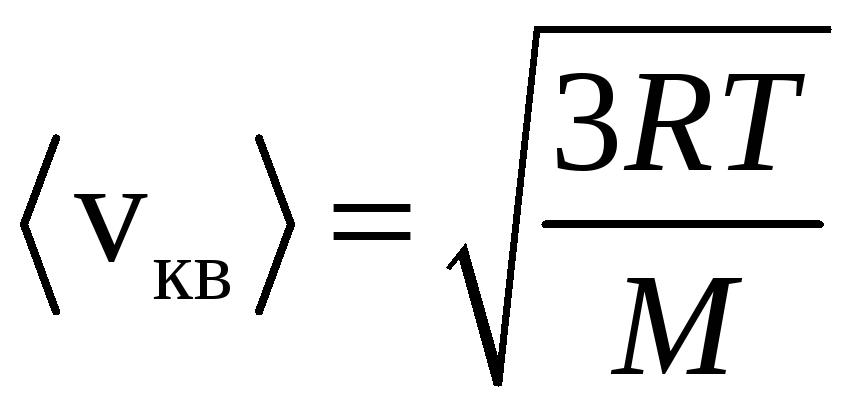 .
.
Из уравнения
состояния газа выразим
![]() ,
так что получим
,
так что получим
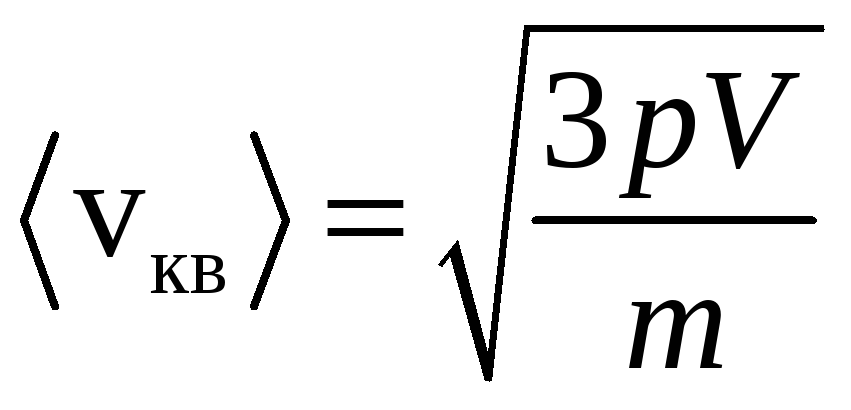 .
.
Найдем
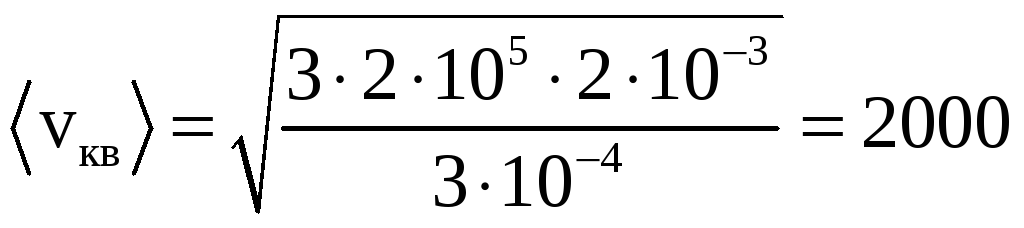 м\с=2 км\с.
м\с=2 км\с.
Ответ: 2 км\с.
9. Масса
![]() каждой из пылинок, взвешенных в воздухе
равна
каждой из пылинок, взвешенных в воздухе
равна
![]() Отношение концентрации
Отношение концентрации
![]() пылинок на высоте
пылинок на высоте
![]() к концентрации
к концентрации
![]() на высоте
на высоте
![]() равно 0,787. температура
равно 0,787. температура
![]() Найти по этим данным значение числа
Авогадро
Найти по этим данным значение числа
Авогадро
![]()
Решение.
Зависимость концентрации частиц от высоты имеет вид
![]() .
.
Для
малой высоты
![]() .
.
Выразим
отсюда
 ,
тогда число Авогадро как отношение
,
тогда число Авогадро как отношение
![]() будет равно
будет равно
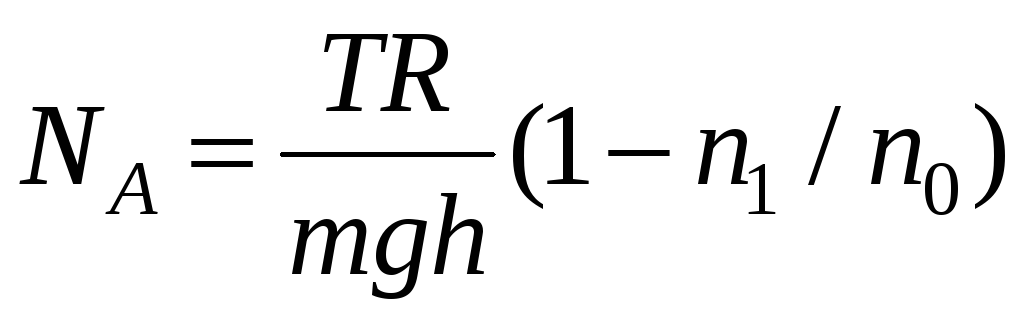 .
.
Найдем
![]() моль-1.
моль-1.
Ответ:
![]() моль-1.
моль-1.
10. Определить
удельные теплоемкости
![]() и
и
![]() газообразного оксида углерода СО.
газообразного оксида углерода СО.
Решение.
В молекуле оксида 2 атома, поэтому число степеней свободы молекулы равно 5.
Удельные теплоемкости можем найти по формулам:
![]() .
.
Найдем
![]() Дж\(кг*К).
Дж\(кг*К).
Ответ:
![]() Дж\(кг*К).
Дж\(кг*К).
11. Кислород находится
под давлением
![]() при температуре
при температуре
![]() Вычислить среднее число
Вычислить среднее число
![]() столкновений молекулы кислорода при
этих условиях за время
столкновений молекулы кислорода при
этих условиях за время
![]()
Решение.
Среднее число столкновений равно отношению средней арифметической скости к длине свободного пробега и равно
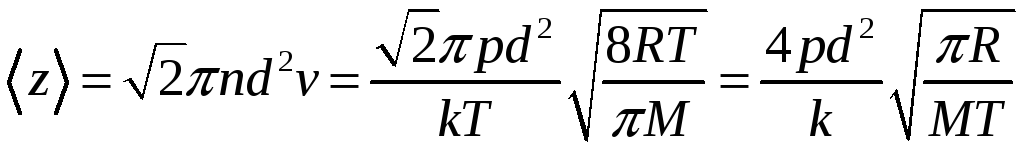 .
.
Найдем
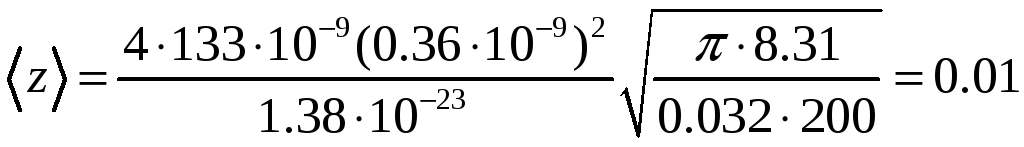
Ответ: 0.01.
12. При адиабатном
сжатии давление воздуха было увеличено
от
![]() до
до
![]() Затем при неизменном объеме температура
воздуха была понижена до первоначальной.
Определить давление
Затем при неизменном объеме температура
воздуха была понижена до первоначальной.
Определить давление
![]() газа в конце процесса.
газа в конце процесса.
Решение.
При
адиабатном процессе
![]() .
Затем при постоянном объеме имеем
.
Затем при постоянном объеме имеем
![]() (по
условию конечная температура равна
начальной).
(по
условию конечная температура равна
начальной).
Получим для давления в конце процесса:
![]() .
.
Найдем
![]() Па=0.26 МПа.
Па=0.26 МПа.
Ответ: 0.26 МПа.
13. Используя
выражение уравнения Ван-дер-Ваальса
для произвольного количества вещества
газа, найти, какую часть вместимости
сосуда составляет собственный объём
молекул газа и определить отношение
внутреннего давления
![]() и давления
и давления
![]() на стенки сосуда. Известно, что в баллоне
вместимостью
на стенки сосуда. Известно, что в баллоне
вместимостью
![]() находится кислород массой
находится кислород массой
![]() при температуре
при температуре
![]() Принять
Принять
![]()
Решение.
Для получения ответа на первый вопрос задачи необходимо найти отношение
k=Vм/V, где Vм - собственный объем молекул.
Собственный объем молекул найдем, воспользовавшись постоянной b Ван-дер-Ваальса, равной учетверенному объему молекул, содержащихся в одном моле реального газа. В уравнении Ван-дер-Ваальса
поправка
vb означает учетверенный объем молекул
всего газа,
![]() .
Отсюда
.
Отсюда
![]()
После вычисления по этой формуле получим
![]()
Следовательно, собственный объем молекул составляет 0.93 % от объема сосуда.
Отношение внутреннего
давления
![]() и давления
и давления
![]() на стенки сосуда найдем как
на стенки сосуда найдем как
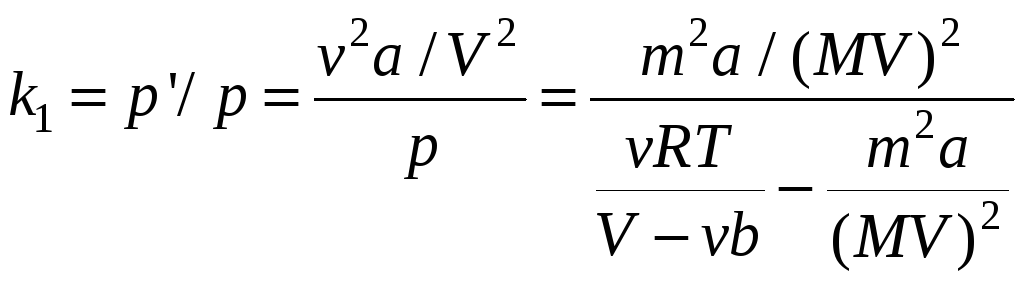
Подстановка чисел даст
![]()
Ответ: к=0.93 %, к1=6.3%.
14. Вычислить
коэффициент диффузии
![]() азота: 1) при нормальных условиях; 2) при
давлении
азота: 1) при нормальных условиях; 2) при
давлении
![]() и температуре
и температуре
![]() Необходимые данные взять из любого
задачника по физике (для ВУЗа)
Необходимые данные взять из любого
задачника по физике (для ВУЗа)
Решение.
Коэффициент диффузии дается формулой
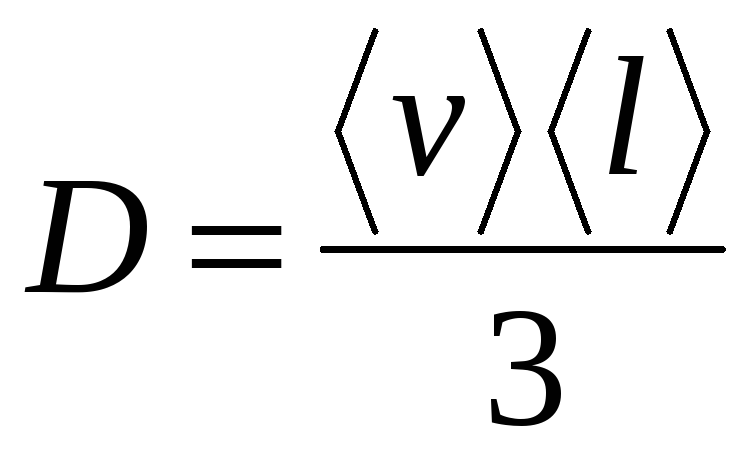 .
.
Здесь средняя арифметическая скорость и средняя длина свободного пробега
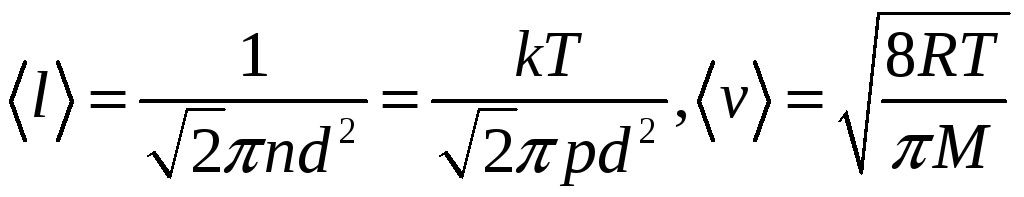 .
.
Получим
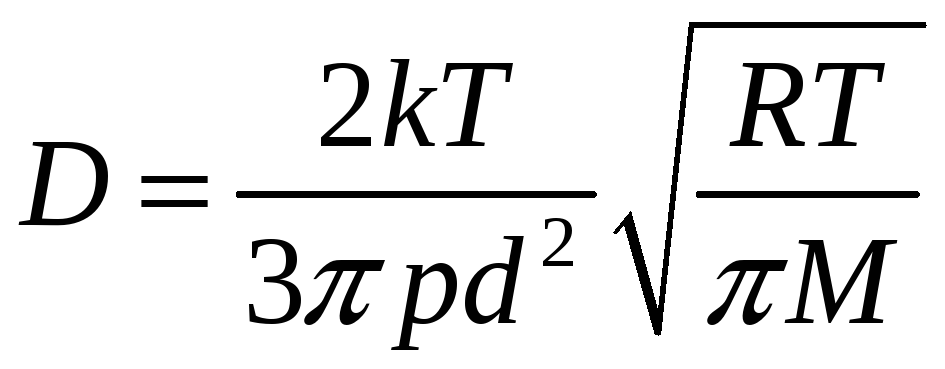 .
.
Найдем
1)
 м2\с,
м2\с,
2)
 м2\с.
м2\с.
Ответ:
![]() м2\с, 2)
м2\с, 2)
![]() м2\с.
м2\с.
Вариант 2.
1. Две материальные
точки движутся согласно уравнениям
![]() и
и
![]() где
где
![]()
![]()
![]()
![]()
![]()
![]() В какой момент времени
В какой момент времени
![]() ускорения этих точек будут одинаковы?
Найти скорости
ускорения этих точек будут одинаковы?
Найти скорости
![]() и
и
![]() точек в этот момент.
точек в этот момент.
Решение.
Найдем ускорение точек как вторые производные координат:
![]() и
и
![]() .
.
Они будут равны
при условии
![]() ,
откуда
,
откуда
![]() с.
с.
Скорости как функции времени даются первой производной координаты и равны
![]() и
и
![]() .
.
Для найденного момента времени получим
![]() м\с и
м\с и
![]() м\с.
м\с.
Ответ:
![]() с,
с,
![]() м\с и
м\с и
![]() м\с.
м\с.
2. Цилиндр,
расположенный горизонтально, может
вращаться вокруг оси, совпадающей с
осью цилиндра. Масса цилиндра
![]() На цилиндр намотали шнур, к которому
привязали гирю массой
На цилиндр намотали шнур, к которому
привязали гирю массой
![]() С каким ускорением будет опускаться
гиря? Какова сила натяжения шнура во
время движения гири?
С каким ускорением будет опускаться
гиря? Какова сила натяжения шнура во
время движения гири?
Решение
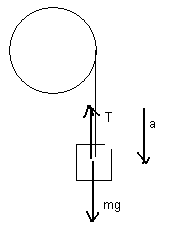
Для
груза по 2-му закону Ньютона
![]() ,
для блока из основного уравнения
вращательного движения
,
для блока из основного уравнения
вращательного движения
![]() .
.
Здесь
момент инерции блока
![]() ,
угловое ускорение вращения
,
угловое ускорение вращения
![]() .
.
Получим
![]() ,
тогда из первого уравнения
,
тогда из первого уравнения
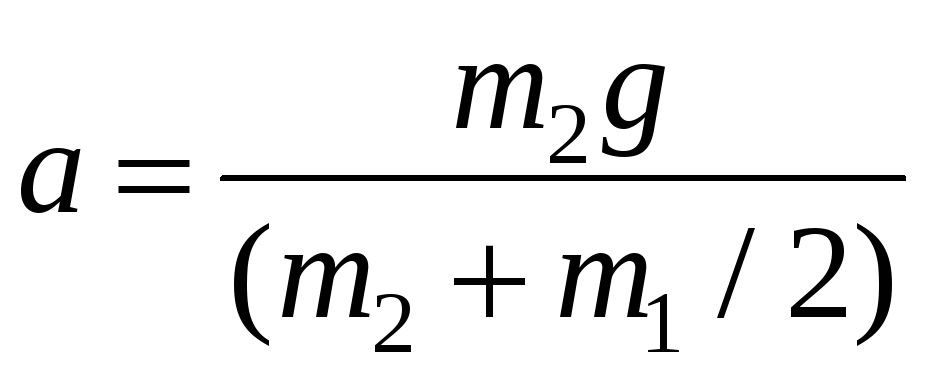 .
.
Найдем
![]() м\с2,
м\с2,
![]() Н.
Н.
Ответ: а=1.4 м\с2, Т=8.4 Н.
3. Шар массой
![]() движется со скоростью
движется со скоростью
![]() и сталкивается с покоящимся шаром массой
и сталкивается с покоящимся шаром массой
![]() Какая работа будет совершена при
деформации шаров? Удар считать абсолютно
неупругим, прямым, центральным
Какая работа будет совершена при
деформации шаров? Удар считать абсолютно
неупругим, прямым, центральным
Решение.
При неупругом ударе выполняется закон сохранении импульса, согласно которому
![]() .
.
Работа по деформации шаров равна разности их кинетических энергий до и после удара, получим
 .
.
Найдем
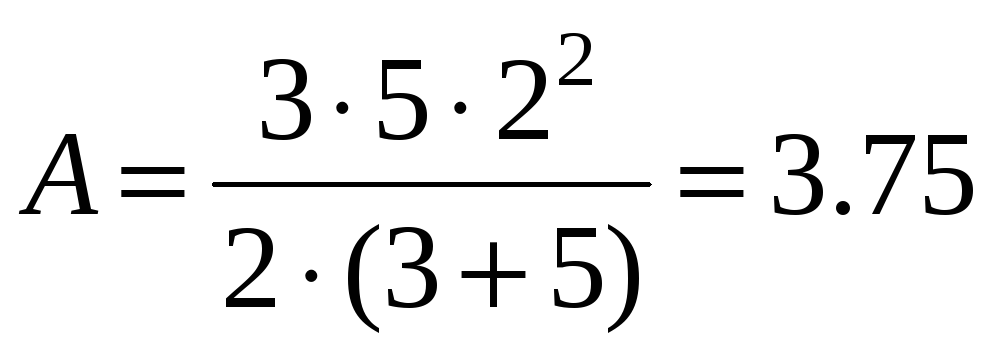 Дж.
Дж.
Ответ: 3.75 Дж.
4. Платформа в виде
диска диаметром
![]() и массой
и массой
![]() может вращаться вокруг вертикальной
оси. С какой угловой скоростью
может вращаться вокруг вертикальной
оси. С какой угловой скоростью
![]() будет вращаться эта платформа, если по
ее краю пойдет человек массой
будет вращаться эта платформа, если по
ее краю пойдет человек массой
![]() со скоростью
со скоростью
![]() относительно платформы?
относительно платформы?
Решение.
По
закону сохранения момента импульса
![]() ,
где
,
где
![]() .
.
Отсюда угловая частота вращения платформы будет равна
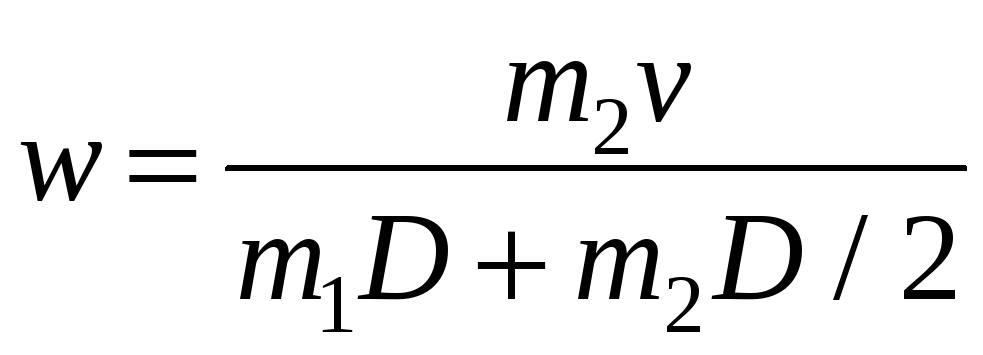 .
.
Найдем
![]() рад\с.
рад\с.
Ответ: 0.195 рад\с.
5. С поверхности
Земли вертикально вверх пущена ракета
со скоростью
![]() На какую высоту она поднимется?
На какую высоту она поднимется?
Решение.
По закону сохранения энергии получим
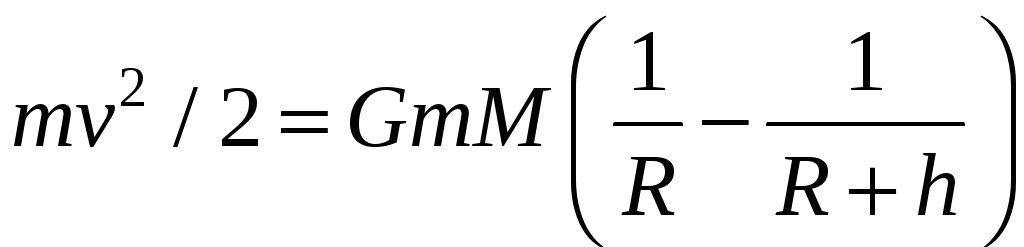 .
.
Отсюда выразим
высоту как
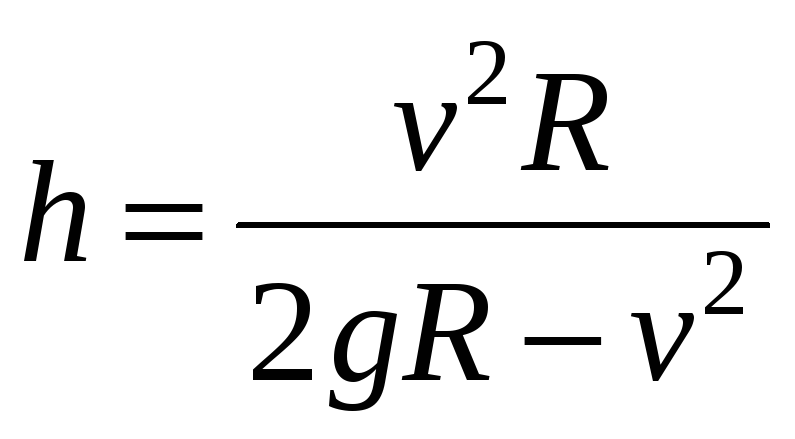 .
.
Найдем
 м=1600 км.
м=1600 км.
Ответ: 1600 км.
6. Определить
количество вещества
![]() и число
и число
![]() молекул кислорода массой
молекул кислорода массой
![]()
Решение.
Количество
вещества равно
![]() ,
а число молекул -
,
а число молекул -
![]() .
.
Найдем
![]() моль,
моль,
![]() .
.
Ответ:
15.625 моль,
![]() молекул.
молекул.
7. Какой объем
![]() занимает смесь азота массой
занимает смесь азота массой
![]() и гелия массой
и гелия массой
![]() при нормальных условиях?
при нормальных условиях?
Решение.
Для смеси уравнение состояния имеет стандартный вид
![]() .
.
Здесь m – масса смеси, М – молярная масса смеси, рассчитывается как
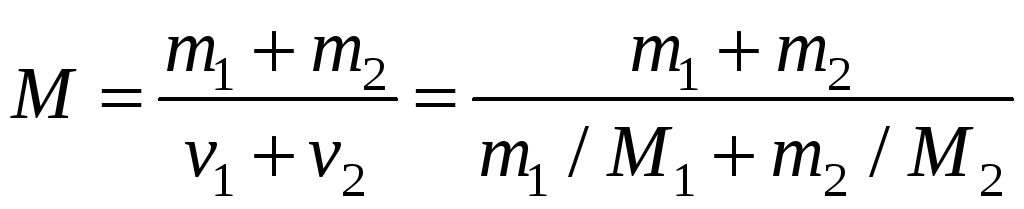 .
.
Получим
![]() .
.
Найдем
![]() м3.
м3.
Ответ: 6.48 м3.
8. При какой
температуре средняя кинетическая
энергия
![]() поступательного движения молекулы газа
равна
поступательного движения молекулы газа
равна
![]() ?
?
Решение.
Средняя кинетическая энергия поступательного движения молекулы равна
![]() ,
поскольку у молекулы 3 поступательных
степени свободы.
,
поскольку у молекулы 3 поступательных
степени свободы.
Отсюда
![]() .
.
Найдем
![]() К.
К.
Ответ: 200 К.
9. На сколько
изменяется давление
![]() при увеличении высоты на
при увеличении высоты на
![]() вблизи поверхности Земли. Температура
вблизи поверхности Земли. Температура
![]() давление
давление
![]() у поверхности Земли нормальное
у поверхности Земли нормальное
![]()
Решение.
Зависимость давления от высоты дается барометрической формулой
![]() .
.
Для малой высоты разложим экспоненту в ряд и получим
![]() .
.
Отсюда найдем
![]() .
.
Получим
![]() Па.
Па.
Ответ: 11.4 Па.
10. Найти удельные
![]() и
и
![]() ,
а также молярные
,
а также молярные
![]() и
и
![]() теплоемкости углекислого газа.
теплоемкости углекислого газа.
Решение.
В молекуле оксида углерода СО2 3 атома, поэтому число степеней свободы молекулы равно 6.
Удельные теплоемкости можем найти по формулам:
![]() ,
тогда как молярные равны
,
тогда как молярные равны
![]()
Найдем
![]() Дж\(кг*К),
Дж\(кг*К),
![]() Дж\(моль*К).
Дж\(моль*К).
