
- •Графические возможности системы MathCad
- •Введение
- •Построение двухкоординатного графика в декартовой системе координат
- •Форматирование двухкоординатного графика
- •Изменение размера двухкоординатного графика
- •Форматирование осей двухкоординатного графика
- •Способы отображения осей двухкоординатного графика
- •Отображение линий сетки на двухкоординатном графике
- •Отображение требуемого числа линий сетки на двухкоординатном графике
- •Вывод числовых значений на осях двухкоординатного графика
- •Установка границ на осях координат
- •Определение координаты точки двухкоординатного графика
- •Использование фоновых линий на двухкоординатном графике
- •Форматирование линий двухкоординатного графика
- •Выбор символа для линии двухкоординатного графика
- •Способы отображения линий двухкоординатного графика
- •Выбор цвета линии
- •Выбор типа линии двухкоординатного графика
- •Выбор толщины линии двухкоординатного графика
- •Название двухкоординатного графика
- •Построение трехкоординатного графика
- •Порядок построения трёхкоординатного графика
- •Построение графиков параметрических поверхностей
- •Форматирование трехкоординатного графика
- •Изменение размера трёхкоординатного графика
- •Выбор ракурса наблюдения
- •Способы отображения трёхкоординатных графиков
- •Границы трёхкоординатных графиков
- •Окрашивание элементов трёхкоординатных графиков
- •Форматирование осей трёхкоординатного графика
- •Форматирование внешнего вида трёхкоординатного графика
- •Освещение трёхкоординатного графика
- •Название трёхкоординатного графика
- •Форматирование оснований трёхкоординатного графика
- •Особенности форматирования контурных и диаграммных графиков
- •Дополнительные возможности оформления трёхмерных графиков
- •Контрольные вопросы
- •Библиографический список
- •Оглавление
Построение двухкоординатного графика в декартовой системе координат
Прямоугольные графики в декартовой системе координат строятся для функций от одной переменной.
Для построения прямоугольных графиков в декартовой системе координат необходимо выполнить следующие операции [4]:
1. Определить выражения, для которых должны быть построены графики. Аргументы функции могут быть представлены переменными типа отрезок или массивами. Функции могут быть заданы в виде аналитических выражений с индексными переменными или в виде массивов.
2. Установить курсор в рабочем поле документа в точке, которая будет соответствовать левому верхнему углу графика, и создать область построения графика.
Область построения двухкоординатного графика можно создать тремя способами:
а) нажатием комбинации клавиш <Shift> +<@>;
б) командой Вставка/ График/ Точка XY (Insert/Graph/ XY Plot) главного меню MathCAD;
в) нажатием кнопки
Точка XY
(XY
Plot)
![]() палитры графиков
палитры графиков![]() (рис.1).
(рис.1).

Рис.1 – Палитра работы с графиками системы MathCAD
3. Выполнить необходимые обозначения в области графика и нажать клавишу <Enter> или щелкнуть левой кнопкой мыши за пределами графической области для построения графика.
При этом под названиями функций, изображаемыми на оси ординат, появляется обозначение кривой соответствующей данной функции.
В одной области графика можно построить до 16 зависимостей функций от одной переменной.
MathCAD позволяет устанавливать мягкие и жесткие границы изменения переменных. Под мягкими понимаются границы, которые MathCAD устанавливает самостоятельно исходя из описания переменных. Жесткие границы устанавливаются пользователем в процессе создания графика: Для этого вместо черных прямоугольников на концах осей следует поставить желаемые значения переменных.
Пример 1
Построить два графика в одной системе координат для явно заданных функций:
![]() и
и
![]()
от одной переменной на отрезке от а=0 до b=8. Для представления данных использовать не менее 80 точек.
Задать пользовательские функции f(x) и у(x):
![]()
![]()
В общем случае функции f(x) и у(x) могут быть различными.
Задать значения начала а и конца b отрезка, на котором будет построен график:
![]()
![]()
Задать требуемое количество точек (например, 80):
![]()
Вычислить расстояние между соседними точками (шаг):
![]()
Задать диапазон изменения переменной х:
![]()
Установить указатель мыши в то место документа, где будет находиться левый верхний угол графика и создать область построения графика (с.4). На экран будет выведен шаблон области построения двухкоординатного графика (рис.2):

Рис.2 – Шаблон области построении двухкоординатного графика
На месте аргумента по оси Х ввести имя аргумента х. На месте черного прямоугольника по оси Y набрать с клавиатуры имя функции f(x) и нажать клавишу <,> (запятая) (рис.3).

Рис.3 – Создание дополнительного знакоместа для добавления имени функции в области построения двухкоординатного графика
В образовавшийся черный прямоугольник (знакоместо или, по другим источникам, – местозаполнитель) по оси Y вписать имя функции у(х) и нажать клавишу <Enter> или щелкнуть левой кнопкой мыши за пределами области построения графика. При этом будут построены два графика в одной системе координат (рис.4).
В частном случае построения двух графиков от одинаковых функций в одной системе координат графики будут наложены друг на друга (рис.5).

Рис.4 – Построение графиков двух различных функций от одной переменной в одной системе координат
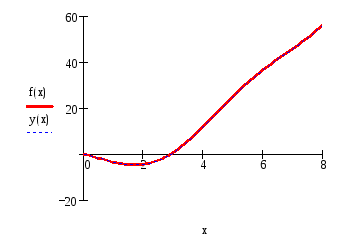
Рис.5 – Построение графиков двух одинаковых функций от одной переменной в одной системе координат
Пример 2
Построить два графика в одной системе координат для функций от одной переменной, но заданных не явно, например: x3 – 1.2ex – y – 1 = 0 и 4.5x – 1.5y – x2 = 0.
Выразить переменную у из первой функции, записать её в виде пользовательской функции MathCAD, обозначить как у1(х):
![]()
Выразить переменную у из второй функции, записать её в виде пользовательской функции MathCAD, обозначить как у2(х):
![]()
Дальнейшие действия аналогичны действиям 2-8 Примера 1.
Пример 3
Построить два графика в одной системе координат для функций, заданных таблично:
|
x |
-0.9 |
-0.434 |
0.015 |
0.9 |
1.81 |
2.646 |
3.46 |
4.28 |
|
y |
8.98 |
2 |
0.23 |
-1.745 |
-3.335 |
-3.56 |
-1.26 |
5.35 |
Ввести значения х. Для этого необходимо:
набрать с клавиатуры
![]()
выполнить команду горизонтального меню Вставка/Матрица (Insert/Matrix) или нажать комбинацию клавиш <Ctrl>+<M>;
в появившемся диалоговом окне Вставить Матрицу (Insert Matrix) (рис.6) следует задать количество строк, равное количеству значений переменной х (в данном случае 8). Количество столбцов следует задать равным единице. На экране получим шаблон одномерного массива (рис.7);
на образовавшиеся знакоместа следует ввести с клавиатуры табличные значения х (рис.8) (переход между знакоместами осуществляется клавишами управления курсором или щелчком левой кнопки мыши по требуемому знакоместу).

Рис.6 – Окно вставки матрицы
![]()
Рис.7 – Шаблон для ввода элементов одномерного массива

Рис.8 – Шаблон элементов одномерного массива, заполненный значениями переменной х
Аналогичным образом вводятся значения у (рис.9):

Рис.9 – Шаблон элементов одномерного массива, заполненный значениями переменной у
Определить положение верхнего левого угла графика и создать область построения двухкоординатного графика любым из возможных способов (с.4).
Чтобы построить два графика в одной системе координат следует:
на месте аргумента по оси Х нужно ввести имя аргумента х;
на месте черного прямоугольника по оси Y набрать с клавиатуры у и нажать клавишу <,> (запятая);
на месте появившегося второго знакоместа по оси Y (рис.10) набрать y, нажать клавишу <Enter> или щелкнуть левой кнопкой мыши за пределами области построения графика.
Вид двух графиков функции, заданной таблично, наложенных друг на друга, представлен на рис.11.
Рис.10 – Создание дополнительного знакоместа для добавления имени функции, заданной таблично, в области построения двухкоординатного графика
Пример 4
Построить графики независимых функций sin(x) для х, изменяющегося от 0 до 2 с шагом 0.2, и cos(y) для y, изменяющегося от 0.5 до 2.8 с шагом 0.1.
Задать интервал изменения аргумента х в виде отрезка:
![]()

Рис.11 – Вид двух графиков функции, заданной таблично, наложенных друг на друга
В данном случае осуществляется построение в одних координатах графиков несвязанных функций для аргументов, имеющих близкий диапазон изменения.
Аналогично задать интервал изменения аргумента y в виде отрезка:
![]()
Определить положение левого верхнего угла графика и создать область построения двухкоординатного графика любым из возможных способов (с.4).
На месте черного прямоугольника по оси абсцисс ввести имя первого аргумента х, нажать клавишу <,> (запятая) и ввести имя второго аргумента у.
Установить указатель мыши на черный прямоугольник по оси ординат и ввести первую функцию sin(x), нажать клавишу <,> (запятая) для перечисления графиков, которые будут построены (при этом образуется новая строка и новое знакоместо для ввода имени второй функции), и ввести вторую функцию cos(y).
Нажать клавишу <Enter> для построения графиков (рис.12).
Пример 5
Построить графики связанных функций двух переменных y=sin(x)-x/3 и x=cos(y)+10

Рис.12 – Вид графиков независимых функций sin(x) и cos(у)
Т.к. обе функции имеют две переменные x и y, целеообразно построение графиков этих функций в координатах x0y. Это можно выполнить двумя способами:
1 способ:
Выразить из обеих функций одну переменную через вторую, например, y через x:
из первой функции
 ,
,из второй функции

Дальнейшие действия аналогичны действиям Примеров 1,2.
способ:
Выразить из обеих функций одну из переменных (ту, которую выразить проще):
из первой функции
 ,
,из второй функции
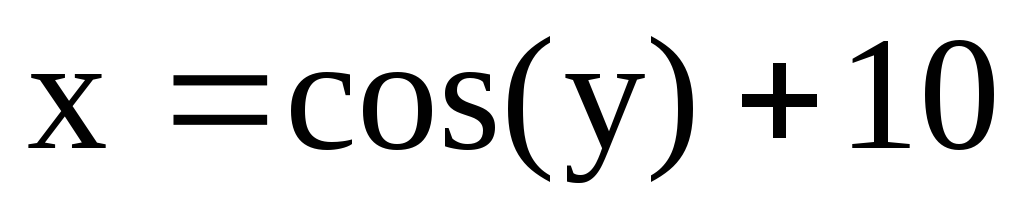 .
.
Выбрать область построения графиков таким образом, чтобы обе функции существовали в выбранных отрезках изменения величин x и y:
функция
 при любых значениях y существует на
отрезке от9
до 11;
при любых значениях y существует на
отрезке от9
до 11;при изменении величины х от 9 до 11 функция
 будет принимать значения от-4
до -2.5.
будет принимать значения от-4
до -2.5.
Для лучшего просмотра графиков целесообразно расширить границы изменения величин x и y:
для х – отрезок от 5 до 15,
для y – отрезок от -5 до -1.
Задать интервалы изменения величин x и y:
![]()
![]()
Определить положение левого верхнего угла графика и создать область построения двухкоординатного графика любым из возможных способов (с.4).
На месте черного прямоугольника по оси абсцисс ввести имя аргумента первой функции х, нажать клавишу <,> (запятая) и ввести выражение для второй функции (cos(y)+10).
На месте черного прямоугольника по оси ординат ввести выражение для первой функции
 ,
нажать клавишу <,> (запятая)
и ввести имя аргумента второй функции
у.
,
нажать клавишу <,> (запятая)
и ввести имя аргумента второй функции
у.Нажать клавишу <Enter> или щелкнуть левой кнопкой мыши за пределами области построения графика для построения графиков (рис.13).
Пример 6
Построить в комплексной плоскости амплитудно-фазовую характеристику объекта регулирования, передаточная функция которого описывается выражением:
![]()
при k=1.2 и T=5.
1. Задать значение переменных k и T:
![]()
![]()

Рис.13 – Внешний вид графиков связанных функций двух переменных x и y
2. Задать диапазон изменения частоты:
![]()
3. Описать комплексную переменную s:
![]()
4. Описать функцию комплексной переменной w(s):
![]()
5. Для построения графиков в комплексной плоскости необходимо вычислить вещественную и мнимую составляющие функции комплексной переменной w(s):
![]()
![]()
6. Определить положение левого верхнего угла графика и создать область построения двухкоординатного графика любым из возможных способов (с.4).
7. При построении
графиков в комплексной плоскости по
оси абсцисс принято откладывать
вещественную составляющую комплексного
числа. Поэтому на месте черного
прямоугольника по оси абсцисс следует
ввести имя вещественной составляющей
![]() .
.
На месте черного прямоугольника по оси ординат ввести имя мнимой составляющей
 .
.Н
 ажать
клавишу <Enter>
или щелкнуть левой кнопкой мыши за
пределами области построения графика
для построения графика (рис.14).
ажать
клавишу <Enter>
или щелкнуть левой кнопкой мыши за
пределами области построения графика
для построения графика (рис.14).
Рис.14 – Внешний вид построенной в комплексной плоскости амплитудно-фазовой характеристики объекта регулирования
Пример 7
Построить полярный
график функции![]() в диапазоне изменения переменнойх
от -10
до 10
с шагом изменения, равным 0,01.
в диапазоне изменения переменнойх
от -10
до 10
с шагом изменения, равным 0,01.
Ввести диапазон изменения переменной х:
![]()
Задать требуемую функцию:
![]()
Определить положение левого верхнего угла графика и создать область построения полярного графика (рис.15) одним из следующих способов:
а) нажатием комбинации клавиш <Ctrl> +<&>;
б) командой Вставка/ График/ Полярный график (Insert/Graph/ Polar Plot) главного меню MathCAD;
в) нажатием кнопки
Полярный
график (Polar
Plot)
![]() палитры графиков
палитры графиков![]() (рис.1).
(рис.1).

Рис. 15 – область построения полярного графика
На месте черного прямоугольника внизу области построения следует ввести имя переменной х, на месте черного прямоугольника слева – имя функции f(x) и нажать клавишу <Enter> или щелкнуть левой кнопкой мыши за пределами области построения графика (рис.16).
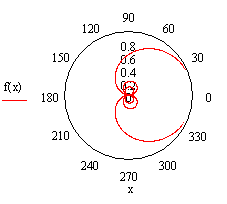
Рис. 16 – Вид полярного графика
