
- •Дифференциальные уравнения 2-го порядка
- •§1. Методы понижения порядка уравнения.
- •§2. Линейное дифференциальное уравнение 2-го порядка.
- •§3. Определитель Вронского.
- •§4. Структура общего решения лоду 2-го порядка.
- •§5. Лоду 2-го порядка с постоянными коэффициентами.
- •§6. Структура общего решения линейного неоднородного дифференциального уравнения (лнду) 2-го порядка.
- •§7. Решение лнду 2-го порядка с постоянными коэффициентами со специальной правой частью.
- •§8. Метод вариации произвольных постоянных (метод Лагранжа).
- •Линейные уравнения высших порядков
- •§1. Однородное уравнение.
- •§2. Линейное однородное дифференциальное уравнение с постоянными коэффициентами.
§5. Лоду 2-го порядка с постоянными коэффициентами.
Дано
лоду 2-го порядка с постоянными
коэффициентами ![]() (5.1), где
(5.1), где ![]() ,
,
![]() .
Согласно предыдущему параграфу общее
решение лоду 2-го порядка легко
определяется, если известны два линейно
независимых частных решения этого
уравнения. Простой метод нахождения
частных решений уравнения с постоянными
коэффициентами предложил Л. Эйлер. Это
метод, который называется методом
Эйлера, состоит в том, что частные решения
ищутся в виде
.
Согласно предыдущему параграфу общее
решение лоду 2-го порядка легко
определяется, если известны два линейно
независимых частных решения этого
уравнения. Простой метод нахождения
частных решений уравнения с постоянными
коэффициентами предложил Л. Эйлер. Это
метод, который называется методом
Эйлера, состоит в том, что частные решения
ищутся в виде ![]() .
.
Подставляя
эту функцию в уравнение (5.1), после
сокращения на ![]() ,
получим алгебраическое уравнение,
которое называется характеристическим:
,
получим алгебраическое уравнение,
которое называется характеристическим:
![]() (5.2)
(5.2)
Функция
![]() будет
решением уравнения (5.1) только при тех
значениях k,
которые являются корнями характеристического
уравнения (5.2). В зависимости от величины
дискриминанта
будет
решением уравнения (5.1) только при тех
значениях k,
которые являются корнями характеристического
уравнения (5.2). В зависимости от величины
дискриминанта ![]() возможны
три случая.
возможны
три случая.
 .
Тогда корни характеристического
уравнения различны:
.
Тогда корни характеристического
уравнения различны: 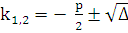 .
Решения
.
Решения  и
и
 будут
линейно независимыми, т.к.
будут
линейно независимыми, т.к.  и общее решение (5.1) можно записать в
виде
и общее решение (5.1) можно записать в
виде  .
.
 .
В этом случае
.
В этом случае  и
и
 .
В качестве второго линейно независимого
решения
.
В качестве второго линейно независимого
решения  можно взять функцию
можно взять функцию 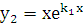 .
Проверим, что эта функция удовлетворяет
уравнению (5.1). Действительно,
.
Проверим, что эта функция удовлетворяет
уравнению (5.1). Действительно,  ,
,
 .
Подставляя эти выражения в уравнение
(5.1), получим
.
Подставляя эти выражения в уравнение
(5.1), получим
![]() или
или
![]() ,
т.к.
,
т.к. ![]() и
и
![]() .
.
Частные
решения ![]() и
и
![]() линейно
независимы, т.к.
линейно
независимы, т.к. ![]() .
Следовательно, общее решение (5.1) имеет
вид:
.
Следовательно, общее решение (5.1) имеет
вид:
![]() или
или
![]() .
.
 .
В этом случае корни характеристического
уравнения комплексно-сопряженные:
.
В этом случае корни характеристического
уравнения комплексно-сопряженные: 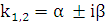 ,
где
,
где  ,
,
 .
Можно проверить, что линейно независимыми
решениями уравнения (5.1) будут функции
.
Можно проверить, что линейно независимыми
решениями уравнения (5.1) будут функции
 и
и
 .
Убедимся, что уравнению (5.1) удовлетворяет,
например, функция y1.
Действительно,
.
Убедимся, что уравнению (5.1) удовлетворяет,
например, функция y1.
Действительно,  ,
,
 .
Подставив эти выражения в уравнение
(5.1), получим
.
Подставив эти выражения в уравнение
(5.1), получим
![]() .
.
Обе
скобки в левой части этого равенства
тождественно равны нулю. Действительно,
![]() ,
,
![]() .
Таким образом, функция
.
Таким образом, функция ![]() удовлетворяет уравнению (5.1). Аналогично
нетрудно убедиться в том, что и
удовлетворяет уравнению (5.1). Аналогично
нетрудно убедиться в том, что и ![]() есть решение уравнения (5.1). Поскольку
есть решение уравнения (5.1). Поскольку
![]() ,
то общее решение
,
то общее решение ![]() будет иметь вид:
будет иметь вид:
![]() .
.
§6. Структура общего решения линейного неоднородного дифференциального уравнения (лнду) 2-го порядка.
Теорема 1. Общее решение лнду 2-го порядка
![]() f(x)
(6.1)
f(x)
(6.1)
представляется
в виде суммы общего решения ![]() соответствующего однородного уравнения
соответствующего однородного уравнения
![]() (6.2)
(6.2)
и
любого частного решения ![]() лнду (6.1).
лнду (6.1).
Доказательство.
Докажем
сначала, что ![]() будет решением уравнения (6.1). Для этого
подставим
будет решением уравнения (6.1). Для этого
подставим ![]() в уравнение (6.1):
в уравнение (6.1): ![]() f(x).
Это равенство является тождеством, т.к.
f(x).
Это равенство является тождеством, т.к.
![]() и
и ![]() f(x).
Следовательно,
f(x).
Следовательно, ![]() есть решение уравнения (6.1).
есть решение уравнения (6.1).
Докажем
теперь, что это решение является общим,
т.е. можно так выбрать входящие в него
произвольные постоянные, что будут
удовлетворяться любые начальные условия
вида: ![]() ,
,
![]() (6.3). Согласно теореме о структуре общего
решения линейного однородного
дифференциального уравнения (лоду)
общее решение уравнения (6.2) можно
представить в виде
(6.3). Согласно теореме о структуре общего
решения линейного однородного
дифференциального уравнения (лоду)
общее решение уравнения (6.2) можно
представить в виде ![]() ,
где
,
где ![]() и
и ![]() – линейно независимые решения этого
уравнения. Таким образом:
– линейно независимые решения этого
уравнения. Таким образом:
![]() и, следовательно, начальные условия
(6.3) можно записать в виде:
и, следовательно, начальные условия
(6.3) можно записать в виде:
![]()
или
![]() (6.4)
(6.4)
Произвольные
постоянные ![]() и
и ![]() определяются из этой системы линейных
алгебраических уравнений однозначно
при любых правых частях, т.к. определитель
этой системы
определяются из этой системы линейных
алгебраических уравнений однозначно
при любых правых частях, т.к. определитель
этой системы ![]() =
= ![]() есть значение определителя Вронского
для линейно независимых решений уравнения
(6.2) при
есть значение определителя Вронского
для линейно независимых решений уравнения
(6.2) при ![]() ,
а такой определитель, как мы видели
выше, отличен от нуля. Определив постоянные
,
а такой определитель, как мы видели
выше, отличен от нуля. Определив постоянные
![]() и
и ![]() из системы уравнений (6.4) и подставив их
в выражение
из системы уравнений (6.4) и подставив их
в выражение ![]() ,
мы получим частное решение уравнения
(6.1), удовлетворяющее заданным начальным
условиям. Теорема доказана.
,
мы получим частное решение уравнения
(6.1), удовлетворяющее заданным начальным
условиям. Теорема доказана.
Докажем еще одну простую теорему, которая часто используется при решении лнду.
Теорема
2.
Если ![]() - решение дифференциального уравнения
- решение дифференциального уравнения
![]() f1(x),
а
f1(x),
а ![]() - решение уравнения
- решение уравнения ![]() f2(x),
то функция
f2(x),
то функция ![]() будет решением уравнения
будет решением уравнения
![]() f1(x)
+ f2(x).
(6.5)
f1(x)
+ f2(x).
(6.5)
Доказательство.
Подставив
функцию ![]() в уравнение (6.5), получим
в уравнение (6.5), получим
![]() f1
+ f2.
Это равенство является тождеством, т.к.
f1
+ f2.
Это равенство является тождеством, т.к.
![]() f1
и
f1
и ![]() f2.
Теорема доказана.
f2.
Теорема доказана.
