
- •Дифференциальные уравнения 2-го порядка
- •§1. Методы понижения порядка уравнения.
- •§2. Линейное дифференциальное уравнение 2-го порядка.
- •§3. Определитель Вронского.
- •§4. Структура общего решения лоду 2-го порядка.
- •§5. Лоду 2-го порядка с постоянными коэффициентами.
- •§6. Структура общего решения линейного неоднородного дифференциального уравнения (лнду) 2-го порядка.
- •§7. Решение лнду 2-го порядка с постоянными коэффициентами со специальной правой частью.
- •§8. Метод вариации произвольных постоянных (метод Лагранжа).
- •Линейные уравнения высших порядков
- •§1. Однородное уравнение.
- •§2. Линейное однородное дифференциальное уравнение с постоянными коэффициентами.
Дифференциальные уравнения 2-го порядка
§1. Методы понижения порядка уравнения.
Дифференциальное уравнение 2-го порядка имеет вид:
![]() .
(1.1)
.
(1.1)
Общим
решением уравнения является семейство
функций, зависящее от двух произвольных
постоянных ![]() и
и ![]() :
:
![]() (или
(или ![]() – общий интеграл дифференциального
уравнения 2-го порядка). Задача Коши для
дифференциального уравнения 2-го порядка
(1.1) состоит в отыскании частного решения
уравнения, удовлетворяющего начальным
условиям: при
– общий интеграл дифференциального
уравнения 2-го порядка). Задача Коши для
дифференциального уравнения 2-го порядка
(1.1) состоит в отыскании частного решения
уравнения, удовлетворяющего начальным
условиям: при ![]() :
:
![]() ,
,
![]() .
Необходимо заметить, что графики решений
уравнения 2-го порядка могут пересекаться
в отличие от графиков решений уравнения
1-го порядка. Однако решение задачи Коши
для уравнений 2-го порядка (1.1) при довольно
широких предположениях для функций,
входящих в уравнение, единственно, т.е.
всякие два решения с общим начальным
условием
.
Необходимо заметить, что графики решений
уравнения 2-го порядка могут пересекаться
в отличие от графиков решений уравнения
1-го порядка. Однако решение задачи Коши
для уравнений 2-го порядка (1.1) при довольно
широких предположениях для функций,
входящих в уравнение, единственно, т.е.
всякие два решения с общим начальным
условием ![]() ,
,
![]() совпадают на пересечении интервалов
определения.
совпадают на пересечении интервалов
определения.
Получить общее решение или решить задачу Коши для дифференциального уравнения 2-го порядка аналитически удается далеко не всегда. Однако в некоторых случаях удается понизить порядок уравнения с помощью введения различных подстановок. Разберем эти случаи.
Уравнения, не содержащие явно независимой переменной
 .
.
Пусть
дифференциальное уравнение 2-го порядка
имеет вид: ![]() ,
т.е. в уравнении (1.1) явно не присутствует
независимая переменная
,
т.е. в уравнении (1.1) явно не присутствует
независимая переменная ![]() .
Это позволяет принять
.
Это позволяет принять ![]() за новый аргумент, а производную 1-го
порядка
за новый аргумент, а производную 1-го
порядка ![]() принять за новую функцию
принять за новую функцию ![]() .
Тогда
.
Тогда ![]() .
.
Таким
образом, уравнение 2-го порядка ![]() для функции
для функции ![]() ,
не содержащее явно
,
не содержащее явно ![]() ,
свелось к уравнению 1-го порядка
,
свелось к уравнению 1-го порядка ![]() для функции
для функции ![]() .
Интегрируя это уравнение, получаем
общий интеграл
.
Интегрируя это уравнение, получаем
общий интеграл ![]() или
или ![]() ,
а это есть дифференциальное уравнение
1-го порядка для функции
,
а это есть дифференциальное уравнение
1-го порядка для функции ![]() .
Решая его, получаем общий интеграл
исходного дифференциального уравнения,
зависящий от двух произвольных постоянных:
.
Решая его, получаем общий интеграл
исходного дифференциального уравнения,
зависящий от двух произвольных постоянных:
![]() .
.
Пример
1.
Решить дифференциальное уравнение ![]() при заданных начальных условиях:
при заданных начальных условиях: ![]() ,
,
![]() .
.
Решение.
Так
как в исходном уравнении в явном виде
отсутствует аргумент ![]() ,
то примем
,
то примем ![]() за новую независимую переменную, а
за новую независимую переменную, а ![]() – за
– за ![]() .
Тогда
.
Тогда ![]() и уравнение приобретает следующий вид
для функции
и уравнение приобретает следующий вид
для функции ![]() :
:
![]() .
.
Это
дифференциальное уравнение с разделяющимися
переменными: ![]() . Откуда следует
. Откуда следует ![]() ,
т.е.
,
т.е. ![]() .
.
Так
как при ![]() и
и
![]() ,
то подставляя начальные условия в
последнее равенство, получаем, что
,
то подставляя начальные условия в
последнее равенство, получаем, что ![]() и
и ![]() ,
что равносильно
,
что равносильно ![]() .
В результате для функции
.
В результате для функции ![]() имеем уравнение с разделяющимися
переменными, решая которое, получаем
имеем уравнение с разделяющимися
переменными, решая которое, получаем
![]() .
Используя начальные условия, получаем,
что
.
Используя начальные условия, получаем,
что ![]() .
Следовательно, частный интеграл
уравнения, удовлетворяющий начальным
условиям, имеет вид:
.
Следовательно, частный интеграл
уравнения, удовлетворяющий начальным
условиям, имеет вид: ![]() .
.
Уравнения, не содержащие явно искомой функции
 .
.
Пусть
дифференциальное уравнение 2-го порядка
имеет вид: ![]() ,
т.е. в уравнение явно не входит искомая
функция
,
т.е. в уравнение явно не входит искомая
функция ![]() .
В этом случае вводят постановку
.
В этом случае вводят постановку ![]() .
Тогда
.
Тогда ![]() и уравнение 2-го порядка
и уравнение 2-го порядка ![]() для функции
для функции ![]() переходит в уравнение 1-го порядка
переходит в уравнение 1-го порядка ![]() для функции
для функции ![]() .
Проинтегрировав его, получаем
дифференциальное уравнение 1-го порядка
для функции
.
Проинтегрировав его, получаем
дифференциальное уравнение 1-го порядка
для функции ![]() :
:
![]() .
Решая последнее уравнение, получаем
общий интеграл заданного дифференциального
уравнения
.
Решая последнее уравнение, получаем
общий интеграл заданного дифференциального
уравнения ![]() ,
зависящий от двух произвольных постоянных:
,
зависящий от двух произвольных постоянных:
![]() .
.
Пример
2.
Найти общее решение уравнения: ![]()
Решение.
В
данное уравнение 2-го порядка явно не
входит искомая функция ![]() ,
следовательно, делаем замену:
,
следовательно, делаем замену: ![]() и
и ![]() .
В результате чего получаем дифференциальное
уравнение 1-го порядка для функции
.
В результате чего получаем дифференциальное
уравнение 1-го порядка для функции ![]() :
:
![]() или
или ![]() ,
являющееся линейным уравнением. Решая
его, получаем:
,
являющееся линейным уравнением. Решая
его, получаем: ![]() или
или
![]() .
Итак, для функции
.
Итак, для функции ![]() получили дифференциальное уравнение
с разделяющимися переменными:
получили дифференциальное уравнение
с разделяющимися переменными: ![]() ,
откуда следует общее решение исходного
уравнения:
,
откуда следует общее решение исходного
уравнения: ![]() .
.
Порядок степени понижается, если удается преобразовать его к такому виду, что обе части уравнения становятся полными производными по
 от каких-нибудь функций. Например, пусть
дано уравнение
от каких-нибудь функций. Например, пусть
дано уравнение  .
Деля обе части на
.
Деля обе части на  ,
получаем
,
получаем  ;
;
 ;
;
 ;
;
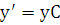 – порядок уравнения понижен.
– порядок уравнения понижен.
