3. Стандартные комбинационные узлы

Стандартные комбинационные узлы электронных устройств исторически появились как первые завершенные функциональные устройства в интегральном исполнении. Фактором, объединяющим все стандартные комбинационные узлы, является возможность их схемотехнической реализации исключительно на логических элементах, либо в отдельном корпусе, либо входящими в состав больших интегральных схем.

По насыщенности дискретных элементов (транзисторов, диодов, резисторов и др.) на кристалле стандартные комбинационные узлы относятся к интегральным схемам (ИС) средней степени интеграции. Число дискретных элементов, расположенных на кристалле интегральной схемы средней степени интеграции (СИС), составляет от 101 до 1000 элементов.

Шифратор. Это  стандартный комбинационный узел, предназначенный для преобразования m-разрядного позиционного кода на входе в n-разрядный двоичный код на выходе, с обязательным условием m > n. Шифраторы различаются по количеству входов m и выходов n и обозначаются: шифратор «из m в n». Например, шифратор «из 10 в 4» выполняет преобразование десятичных цифр, поступающих на его входы, в двоичные, формируемые на выходах. Двоичное число, формируемое на выходах шифратора, может отображаться как прямым, так и инверсным кодами.

Шифратор, у которого количество входов и выходов связано условием n = log₂m, называется полным шифратором.

Шифратор, формирующий на выходах код старшей десятичной цифры при одновременном поступлении на его входы нескольких запросов, называется приоритетным шифратором.

Операция шифрации ставит в соответствие каждому из 2^m  k_m рабочих наборов входных переменных один из 2ⁿ  k_n рабочих наборов выходных переменных, следовательно, в результате шифрации выполняется «сжатие» информации, так как m > n, а 2^m  k_m > 2ⁿ  k_n .

При шифрации, на примере шифратора «из 10 в 4», 10-разрядный входной двоичный код, имеющий 1014 безразличных наборов входных переменных, преобразуется в однозначно ему соответствующий 4-разрядный выходной код, имеющий шесть безразличных наборов, следовательно, для шифратора «из 10 в 4» выполняются условия: 10 > 4, a 1024 – 10 > 16  10.

Задача 2.2. Синтезировать приоритетный шифратор прерываний от восьми устройств. Запросы на прерывания в шифратор поступают на входы Х₀,…,Х₇. На выходах Y_i формируется прямой двоичный код номера входа Х_i, по которому поступил запрос на прерывание. Шифратор обладает дополнительными функциями:

 вход Е разрешает формирование кода на выходах Y_i;

 выход Р указывает на обработанный запрос на прерывание;

 выход V указывает на отсутствие запросов на прерывания.

Синтез шифратора выполнить в базисе И, ИЛИ, НЕ.

На основании условий задачи сформирована таблица истинности переключений приоритетного шифратора прерываний (табл. 2.2).

Таблица 2.2

Таблица истинности переключений приоритетного шифратора «из 8 в 3»

Активный уровень на входах	Логические уровни
	на входах									на выходах
	Е	х0	х1	х2	х3	х4	х5	х6	х7	Y2	Y1	Y0	Р	V
Произвольных	0	*	*	*	*	*	*	*	*	0	0	0	0	0
х0	1	1	0	0	0	0	0	0	0	0	0	0	1	0
х0 … х1	1	*	1	0	0	0	0	0	0	0	0	1	1	0
х0 … х2	1	*	*	1	0	0	0	0	0	0	1	0	1	0
х0 … х3	1	*	*	*	1	0	0	0	0	0	1	1	1	0
х0 … х4	1	*	*	*	*	1	0	0	0	1	0	0	1	0
х0 … х5	1	*	*	*	*	*	1	0	0	1	0	1	1	0
х0 … х6	1	*	*	*	*	*	*	1	0	1	1	0	1	0
х0 … х7	1	*	*	*	*	*	*	*	1	1	1	1	1	0
Активные уровни отсутствуют	1	0	0	0	0	0	0	0	0	0	0	0	0	1

По условию задачи шифратор  приоритетный, активный уровень по входу с более высоким индексом блокирует все активные уровни у входов с меньшим индексом, поэтому в табл. 2.2 логические значения аргументов, расположенные левее выделенных заливкой «1», не могут переопределять код на выходе (они обозначены «*») и, следовательно, могут принимать произвольные состояния. Для шифратора «из 8 в 3» 8 > 3, a 256 – 8 > 8  8, правая часть последнего неравенства равна нулю, следовательно, шифратор является полным.

Минимальные уравнения, соответствующие табл. 2.2, отображают функции для выходов приоритетного шифратора:

;

;

;

;

.

Для построения принципиальной схемы в уравнениях (2.8) необходимо однозначно сопоставить импликанты и логические элементы, соблюдая при этом иерархию расположения скобок (см. гл. 1). В соответствии с иерархией расположения логических элементов подключить на входы принципиальной схемы инверторы, явно не указанные в (2.8), как показано на рис. 2. 11.

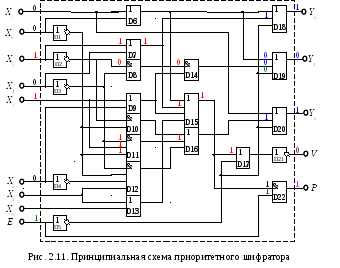
Принципиальная схема приоритетного шифратора (рис. 2.11) включает три ступени. Первая ступень  инверторы (элементы D1, …, D4), обеспечивающие формирование шифрованного двоичного кода на выходах. Вторая ступень  дизъюнкторы и конъюнкторы (элементы D6, …, D16), формирующие двоичный код для передачи на выходы. Третья ступень  дизъюнкторы, конъюнкторы и инверторы (элементы D6, D18, …, D22), осуществляющие формирование состояния шифратора на его выходах по разрешающему сигналу на входе Е.

Правильность соединений логических элементов в принципиальную схему приоритетного шифратора определяется подстановкой логических уровней на входы узла с дальнейшим определением состояния как на выходе каждого из логических элементов, так и на выходе узла. На рис. 2.11 показано воздействие активного уровня на входе Х₅, активные уровни на входах и выходах логических элементов определяют правильный код на выходах шифратора.

Использование условного графического обозначения шифраторов, как показано на рис. 2. 12, при построении вычислительных систем упрощает начертание принципиальных схем последних.

Один приоритетный шифратор позволяет декодировать прерывания от восьми устройств. Для увеличения количества устройств, от которых формируются приоритетные прерывания, используется каскадное соединение шифраторов. При каскадном соединении шифраторов, как показано на рис. 2.13, устройства с более высоким приоритетом (порядковые номера которых 8…15) подключаются на входы элемента D1, а младшие (порядковые номера 0…7)  соответственно на D2.

При отсутствии запросов на прерывания от устройств с порядковыми номерами 8…15 на выходе V элемента D1 формируется высокий уровень, разрешающий преобразования шифратору D2, и одновременно на выходе P элемента D1 формируется низкий уровень, устанавливающий старший разряд кода К3 в состояние логического 0, следовательно, на выходах К2…К0 формируется двоичный код активного входа элемента D2.

Вход Е элемента D1 является входом, разрешающим преобразования для всего каскадного соединения шифраторов.

Дальнейшее увеличение количества шифраторов в каскадном соединении приводит к усложнению дополнительной схемы формирования состояний кодов K_i.

Шифраторы используются для операций:

• формирования приоритетных прерываний;

• преобразования элементов позиционного кода в стандартный двоичный код (ввод с клавиатуры);

• формирования двоичного числа, определяющего старший разряд, в котором расположена единица;

• нормализации чисел с плавающей запятой;

• передачи данных между устройствами при ограниченном числе соединительных линий.

Вывод. Шифратор, как интегральная схема средней степени интеграции, выполняет основную функцию преобразования активных уровней позиционного кода, когда каждое устройство обладает собственной физической цепью, в двоичный код, представляющий номер активного устройства. Такое преобразование упрощает цифровую обработку требований от устройства, активизировавшего свой выход.

Один из наиболее ярких примеров использования шифратора в вычислительной технике  формирование прерывания от устройства (двоичное число), сформировавшего активный уровень на своём индивидуальном выходе (позиционный код).

Дешифратор. Это стандартный комбинационный узел, используемый для преобразования m-разрядного двоичного кода на входе в n-разрядный позиционный код на выходе, с обязательным условием m < n. Особенность работы дешифратора  формирование активного уровня на одном определённом выходе, который соответствует двоичной комбинации входящих сигналов. Активными на выходах могут быть как уровни логического 0, так и уровни логической 1.

Дешифраторы различаются по количеству входов m и выходов n и обозначаются: дешифратор «из m в n». Например, дешифратор «из 4 в 10» выполняет преобразование двоичных кодов, поступающих на его входы, в десятичные цифры, формируемые на выходах.

Дешифратор, у которого количество входов и выходов связано условием n = 2^m, называется полным дешифратором.

При дешифрации, на примере дешифратора «из 4 в 10», 4-разрядный входной двоичный код, имеющий 6 безразличных наборов входных переменных, преобразуется в однозначно ему соответствующий 10-разрядный выходной код, имеющий 1014 безразличных наборов, так как для дешифратора «из 4 в 10» 4 < 10, a 16  10 < 1024 – 10.

Задача 2.3. Синтезировать полный дешифратор, обладающий тремя входами: Х₀, Х₁, Х₂. Двоичное число на входах дешифратора активизирует выход Y_i, номер которого определяет минтерм входных переменных, при этом активный логический уровень выхода  высокий. Синтез шифратора выполнить в базисе И, ИЛИ, НЕ.

На основании условий задачи сформирована таблица истинности переключений дешифратора «из 3 в 8» (табл. 2.3), на основании которой сформированы минтермы трёх переменных, создающие функции на выходах:

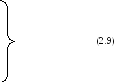
Т

Совокупность минтермов (2.9) позволяет построить принципиальную схему (рис. 2.14), представив каждый из минтермов конъюнктором и подключив на входы принципиальной схемы инверторы, явно не приведённые в (2.9).

Анализ построения принципиальной схемы рис. 2.14 определяет две последователь-

аблица 2.3

Таблица истинности переключений

дешифратора «из 3 в 8»

Логические уровни
На входах			На выходах
х2	х1	х0	Y0	Y1	Y2	Y3	Y4	Y5	Y6	Y7
0	0	0	1	0	0	0	0	0	0	0
0	0	1	0	1	0	0	0	0	0	0
0	1	0	0	0	1	0	0	0	0	0
0	1	1	0	0	0	1	0	0	0	0
1	0	0	0	0	0	0	1	0	0	0
1	0	1	0	0	0	0	0	1	0	0
1	1	0	0	0	0	0	0	0	1	0
1	1	1	0	0	0	0	0	0	0	1

ные ступени при переключении логических элементов, что задаёт время срабатывания линейного дешифратора 2T_п.

Принципиальная схема дешифратора содержит однотипные конъюнкторы, каждый из которых реализует один из минтермов. Такая схема построения дешифратора называется линейным дешифратором. Линейный дешифратор содержит одну ступень преобразования, не считая инверторов, и так как его минимальные уравнения  минтермы, следовательно, линейный дешифратор произвольной сложности должен содержать К = 2^m конъюнкторов (без учёта инверторов), а каждый конъюнктор должен иметь m входов, где m  количество входов дешифратора.

Безошибочность соединений логических элементов в принципиальную схему дешифратора определяется подстановкой логических уровней на входы узла с дальнейшим определением состояния на его выходах. На рис. 2.14 показано воздействие двоичного кода «011», формирующего минтерм и активизирующего выход Y₃.

Для уменьшения количества логических элементов при схемотехнической реализации дешифратора возможна операция факторизации для каждого из минтермов:

; ;

Совокупность минтермов (2.10) позволяет построить принципиальную схему, представив каждый из минтермов двумя двухвходовыми конъюнкторами. Такая схема построения дешифратора называется пирамидальным дешифратором и показана на рис. 2.15, где подключены дополнительные инверторы, явно не приведённые в (2.10).

Анализ построения принципиальной схемы (рис. 2.15) определяет три последовательные ступени при переключении логических элементов, что задаёт время срабатывания пирамидального дешифратора 3T_п.

Элементы D4, …, D7 дешифрируют два младших разряда, а элементы D8, …, D15 формируют активный уровень на одном из выходов дешифратора Y₀, …, Y₇. Для увеличения количества выходов в два раза необходимо к каждому существующему выходу добавить по два конъюнктора с учётом прямого и инверсного значений состояния старшего разряда Х₃, следовательно, каждая последующая ступень содержит в два раза больше элементов, чем предыдущая, а структура дешифратора  пирамидальная. Для пирамидального дешифратора произвольной сложности количество элементов (без учёта инверторов)

(2.11)

где m  количество входов дешифратора.

Используя уравнения (2.10) в качестве исходных, объединим их знаком дизъюнкции с аргументом Х₃ в инверсном значении для выходов Y₀, …, Y₇ и в прямом  для выходов Y₈, …, Y₁₅, следовательно, полученные минтермы образуют уравнения дешифратора «из 4 в 16»:

; ;…;

;

На основании (2.12) можно сформировать уравнение общего вида для выхода n = 2 , если m  количество входов дешифратора:

. (2.13)

Используя двухразрядные функции в качестве сокращённых обозначений, можно представить уравнения выходов дешифратора «из 4 в 16»:

Двухразрядные функции a_i и b_i реализуются дополнительными дешифраторами, каждый из которых выполняет дешифрацию половины входящих разрядов:

Совокупность уравнений (2.14) и (2.15) позволяет построить принципиальную схему дешифратора (рис. 2.16).

На рис. 2.16 показано три последовательные ступени, что определяет время срабатывания матричного дешифратора 3T_п.

Принципиальная схема содержит двухвходовые конъюнкторы, при этом элементы D1,…, D4 дешифрируют два младших разряда и формируют на своих выходах общие уровни b_i, а элементы D5, …, D8  выполняют дешифрацию двух старших разрядов и формируют уровни a_i. Сигналы a_i и b_i совместно формируют значения соответственно столбцов и строк, как указано в (2.14). На каждом пересечении сигналов a_i и b_i установлен конъюнктор (элементы D9, …, D24), формирующий логический уровень на соответствующем выходе Y_i дешифратора, как указано в (2.15). Схема такого дешифратора называется матричным (прямоугольным) дешифратором и показана на рис. 2.16.

Структурно матричный дешифратор состоит из двух пирамидальных дешифраторов первой ступени и конъюнкторов, формирующих сигналы на выходах, поэтому его можно кратко назвать матричный дешифратор «m x n».

Реализация одинаковой сложности дешифраторов различными способами (линейным, пирамидальным или матричным) требует различного количества логических элементов (табл. 2.4).

Таблица 2.4

Количество двухвходовых конъюнкторов, требующихся

для реализации дешифраторов различной сложности*

Сложность	Количество логических элементов при способе реализации
	линейном	пирамидальном	матричном
«Из 2 в 4»	4	4	4
«Из 3 в 8»	16	4 + 8 = 12	4 + 8 = 12
«Из 4 в 16»	48	4 + 8 + 16 = 28	4 + 4 + 16 = 24
«Из 10 в 1024»	9216	2044	1144

* Без учёта количества инверторов.

Для упрощения начертания принципиальных схем используется условное графическое обозначение дешифратора (рис. 2.17).

Наличие дополнительного входа разрешения дешифрации Е, как показано на рис. 2.17,б, позволяет наращивать количество дешифрируемых разрядов, используя при этом стандартные дешифраторы «из 2 в 4», «из 3 в 8» или «из 4 в 16».

Схемы с наращиваемыми разрядами называются каскадированием, а количество линейных и/или пирамидальных дешифраторов определяется из условия

n₁+ n₁+… n_n

, (2.16)

где n₁, n₂, …, n_i  разрядность (число входов) стандартного линейного и/или пирамидального дешифратора на i-й ступени дешифрации при условии n₁ + n₂ + …+ n_i = n  разрядность кодов до дешифрации.

Для наращивания количества дешифрируемых разрядов используется каскадное соединение дешифраторов (рис. 2.18), позволяющее выделить дешифратор старших разрядов (элемент D1) и дешифраторы младших разрядов (элементы D2, …, D5). Дешифратор старших разрядов формирует разрешение работы для одного из дешифраторов младших разрядов, и тем самым производится декодирование всего двоичного числа.

В общем случае дешифраторы старших разрядов формируют разрешения преобразований для дешифраторов младших разрядов, что можно отобразить графически (рис. 2.19).

Дешифраторы используются для операций:

• выбора устройства, номер которого указан двоичным числом;

• дешифрации кода команды;

• выбора ячейки памяти, адрес которой указан в операнде;

• реализации логических вычислений;

• управления мультиплексированием и демультиплексированием.

Вывод. Дешифратор, как интегральная схема средней степени интеграции, выполняет основную функцию выбора (активации) требуемого устройства среди многих других, при этом номер активизируемого устройства определяется двоичным числом.

51