
Экономика
.pdfЗадачи
Вычисление параметров рыночного равновесия. |
|
|
||||||||
1. |
Заполните пустые строки в табл.2.2. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Таблица 2.2 |
|
|
|
|
|
К задаче 1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Цена |
|
Объем |
Объем |
|
Про- |
|
Дефи- |
Объем |
|
Выручка |
P, руб. |
предложе- |
спроса |
|
фицит |
|
цит |
продаж Q |
|
TR, руб. |
|
|
|
ния QS, шт. |
QD, шт. |
|
|
|
|
|
|
|
25 |
|
|
350 |
|
|
|
|
|
|
6 500 |
27 |
|
|
|
|
|
|
70 |
275 |
|
|
|
|
290 |
355 |
|
|
|
|
|
|
9 280 |
38 |
|
315 |
315 |
|
|
|
0 |
|
|
11 970 |
40 |
|
|
|
|
120 |
|
|
280 |
|
|
2.На рынке товара x равновесная цена установилась на уровне 240 руб. за единицу товара при объеме потребления 1 500 ед. товара. Известно также, что продавцы предлагают 1 200 ед. товара при цене 200 руб., при этом на рынке наблюдается дефицит в размере 200 ед. товара. Выведите линейные функции спроса и предложения для данного рынка.
3.На конкурентном рынке существует две группы покупателей.
Функция спроса первой группы описывается уравнением PD1 = 160 – 4Q1, второй – PD2 = 120 – 6Q2. Функция предложения имеет вид PS = 46 + 0,4Q. Найдите параметры равновесия на рынке. Какой объем потребления приходится на каждую группу покупателей?
4.На конкурентном рынке функция спроса описывается уравне-
нием QD 220 2P , функция предложения – QS 150 3P . Как изменятся параметры равновесия на рынке если:
спрос уменьшится на 10 %;
покупатели будут готовы платить за каждую единицу товара на 12 руб. больше;
количество продавцов на рынке уменьшится вдвое.
5. При цене в 12 000 руб. за тонну на рынке продается 480 т меди. Выведите функцию спроса на медь, предполагая, что она линейная, если центовая эластичность спроса равна ~ 0,4.
21
Вычисление дополнительного выигрыша потребителя и производителя.
6. Функции спроса и предложения на конкурентном рынке имеют вид: QD 30 5P , QS 40P 15. Найдите точку равновесия на рын-
ке, излишки потребителя и производителя.
7. Функции спроса и предложения на конкурентном рынке имеют вид: QD 50 5P , QS 10P 5 . Определите величину дополнитель-
ного выигрыша потребителя и производителя.
Задачи на определение последствий введения налогов и субсидий.
8. Функция спроса на конкурентном рынке описывается уравнением QD 220 2P , функция предложения – QS 150 3P . Государ-
ство ввело налог в размере 4 руб. с каждой единицы товара, который уплачивает продавец. Определите, как изменятся параметры равновесия на рынке после введения налога. Какую сумму налоговых поступлений получит государство? Как распределится налоговое бремя между продавцом и покупателем?
9. Как изменятся параметры равновесия на рынке, если государство введет субсидию в размере 6 руб. на каждую единицу товара, которую получает покупатель? Функции спроса и предложения на данном
рынке имеют вид: QS 50 P , QD 250 4P . Как распределится
получение субсидии между продавцом и покупателем?
10. Функции спроса и предложения на конкурентном рынке имеют вид: PD 80 1,25Q , PS 10 0,5Q . Если государство установит «по-
толок» цен в размере 20 руб. за единицу товара, то какая ситуация возникнет на рынке?
Расчет эластичности спроса и предложения.
11. Функция спроса имеет вид: QD 100 2P . Коэффициент эла-
стичности спроса по цене: EDP 2 . Определите цену, при которой
спрос достигает заданного коэффициента эластичности.
12. При цене товара P = 6 и доходе I = 200 определите эластичность спроса по доходу на данный товар, если функция спроса имеет вид:
QD 120 4P 1,5I .
13. Функция спроса имеет вид: QD 60 2P 0,8I . Определите
эластичность спроса по доходу на данный товар, если цена товара равна P = 3, доход составляет I = 100.
22
14.Функция спроса на товар задана уравнением QD = 200 – 1,5Px +
+0,5Py. В точке равновесия цены товаров соответственно равны Px = 30, Py = 100. Определите перекрестную эластичность спроса на товар x по цене на товар y в точке равновесия и характер взаимосвязи товаров.
15.Определите перекрестную эластичность спроса на товар x по цене на товар y в точке равновесия и характер взаимосвязи товаров, ес-
ли функция спроса на товар задана уравнением QD 400 3Px Py .
В точке равновесия цены товаров соответственно равны Px = 60,
Py = 200.
16. Задана функция предложения: QS 7P 1. Определите ценовую эластичность предложения при Р = 10 000.
Темы реферативных докладов (эссе)
1.Охарактеризуйте экономический смысл излишка потребителя и производителя. Почему определение точного абсолютного значения этих величин затруднено?
2.От чего зависит распределение налогового бремени между потребителями и производителями при введении потоварного налога?
3.Какое значение имеет теория эластичности для определения ценовой стратегии фирмы?
4.Какую роль играет эластичность для определения налоговой политики государства?
5.В каком случае в паутинообразной модели равновесие будет устойчивым?
23
Тема 3. Основы теории потребительского поведения
Содержание темы
Теория потребления исходит из того, что цель каждого потребителя –
максимизация полезности.
Полезность (U) – способность экономического блага удовлетворять какую-либо человеческую потребность.
К определению точки потребительского оптимума, т.е. набора товаров, приносящих потребителю максимальную полезность в рамках ограниченного бюджета, существует два подхода: кардиналистский (количественный) и ординалисткий (порядковый).
Кардиналистский подход подразумевает возможность измерять полезность товаров в количественных показателях (ютилях).
Функция полезности – зависимость между количественно выраженной удовлетворенностью потребителя использованными благами и объемами потребления этих благ:
U = U (x, y, …, n),
где x, y, …, n – объемы потребления благ.
Общая полезность (TU) – величина, характеризующая совокупную (суммарную) удовлетворенность от потребления данного количества благ за определенный период времени.
Предельная полезность (MU) – прирост общей полезности при увеличении потребления некоторого блага на единицу:
MU TU или MU TU ' .Q
Закон убывания предельной полезности – в одном непрерывном акте потребления каждая следующая потребляемая единица блага приносит потребителю меньшую полезность, а при насыщении потребности предельная полезность равна нулю (при прочих равных условиях).
Условие равновесия потребителя (в соответствии с кардина-
листской концепцией) достигается при:
24
MU y MU x , Py Px
где MUy, MUx – предельные полезности последних приобретенных единиц благ y и x; Py, Px – цены соответствующих благ.
Ординалистский подход исходит из того, что дать количественную оценку полезности каждого блага сложно; проще ранжировать их от наименее полезного к наиболее полезному или наоборот.
Кривая безразличия показывает |
Y |
|
||||
все возможные |
комбинации |
двух |
|
|||
|
|
|||||
благ, выбор среди которых безразли- |
|
|
||||
чен, потому что они обеспечивают |
|
|
||||
одинаковую полезность для потреби- |
|
y |
||||
теля (рис.3.1). |
|
|
|
|
U3 |
|
|
|
|
|
U2 |
||
Предельная |
норма |
замещения |
y– |
|||
U1 |
||||||
(MRS) характеризует количество од- |
|
|||||
|
x |
|||||
|
|
|
|
|
||
ного блага y, от которого готов отка- |
|
|
||||
заться потребитель ради |
увеличения |
|
X |
|||
потребления другого блага x на до- |
Рис.3.1. Карта кривых безразличия |
|||||
полнительную единицу, |
при |
этом |
|
|
||
не потеряв в полезности: |
|
|
|
|
||
MRSxy yx .
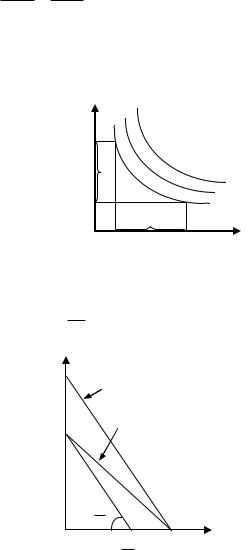
Линия бюджетного ограничения x и y, доступных потребителю Y при заданном уровне дохода I и ценах Рх, Ру (рис.3.2):
I Px x Py y
|
|
I |
|
Px |
|
|
I |
|
или |
y |
|
x. |
|
|
|
||
|
Py |
|||||||
Py |
Py |
|
||||||
|
|
|
|
|
|
|
||
– множество наборов двух благ
Сдвиг бюджетной линии при изменении дохода
(доход увеличился)
Сдвиг бюджетной линии при изменении цены
(цена на товар X уменьшилась)
Увеличение (уменьшение) дохода приводит к сдвигу бюджетного ограничения вверх (вниз). Изменение цены одного товара приводит к изменению угла наклона бюджетного ограничения.
Px Py
I X
Px
Рис.3.2. Линия бюджетного ограничения
25
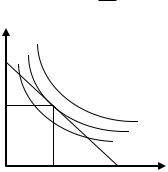
Равновесие потребителя (в соответствии с ординалистской концепцией полезности) достигается в точке касания линии бюджетного ограничения и кривой безразличия (рис.3.3), поскольку при этом потребитель достигает самой высокой из возможных при данном уровне дохода кривых безразличия. При этом выполняется условие:
MRSxy Px . Py
Y
O
U3
U1 U2
X
Рис.3.3. Равновесие потребителя в ординалистской теории
Если функция полезности потребителя имеет вид: U (x, y) xa yb , а располагаемый доход потребителя I Px x Py y , то оптимальный потребительский набор можно определить по правилу долей:
x |
a I |
, y |
a |
|
I |
. |
||
|
|
|
|
|
||||
|
a b P |
|
a b P |
|||||
|
|
|
x |
|
|
|
y |
|
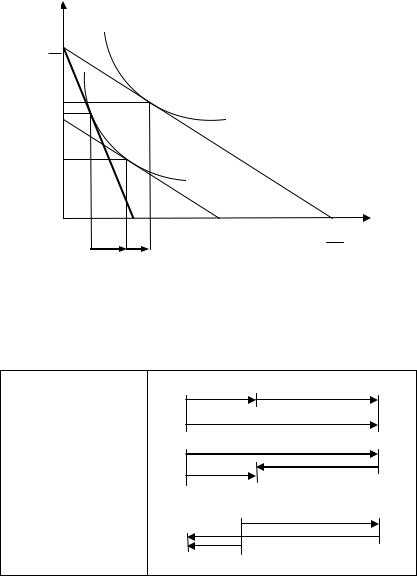
Изменение цены какого-либо товара влияет на объем спроса через эффект замены и эффект дохода (рис.3.4). Эффект дохода состоит в следующем: если цена товара снижается, то покупателю требуется выделять на приобретение того же количества данного товара меньшую часть бюджета, что ведет к увеличению реального дохода. Эффект замещения выражается в следующем: при снижении цены одного товара происходит относительное изменение цен, приводящее к увеличению потребления относительно подешевевшего товара.
26
Y
I
PY
E1
E0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U1 |
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
I ' |
|
|
X |
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
PX |
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
P |
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
' |
|
|
|
|
Эффект |
Эффект |
|
|
|
|
|
P |
|
|
|
||
|
|
|
|
|
X |
|
||||||
замещения |
дохода |
|
|
|
|
|
|
|
|
|
||
Рис.3.4. Эффект дохода и эффект замещения (по методу Дж. Хикса)
Для нормальных товаров эффект дохода и эффект замещения суммируются, для низкокачественных товаров вычитаются (табл.3.1).
Таблица 3.1
Эффект дохода и эффект замещения для разных групп товаров
Эффект |
|
Эффект |
замещения |
|
дохода |
|
|
|
Нормальный товар |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общий эффект |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эффект замещения |
|
|
||||||
Низкокачественный то- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вар |
Общий |
|
|
|
Эффект |
|
||||||
|
|
|
|
дохода |
|
|
||||||
|
эффект |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эффект замещения |
|
||||||
Товар Гиффена |
|
|
|
|
|
|
|
|
|
|
|
|
Общий |
|
|
Эффект дохода |
|
|
|
||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
эффект |
|
|
|
|
|
|
|
|
|
||
27

|
Примеры решения задач |
Задача |
1. Совокупная полезность задается уравнением: |
1 |
2 |
TU 12y 3 x 3 . Доход потребителя I составляет 54 ден. ед. Цены товаров: Px = 2, Py = 3. Определите количество товаров y и x в состоянии
равновесия. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Составим уравнение бюджетной линии: I Px x Py y . |
54 2x 3y . |
|||||||||||||||||||||||||||||||||||||||||||||||
Рассчитаем предельную полезность товара х. Для этого возьмем |
||||||||||||||||||||||||||||||||||||||||||||||||
частную производную функции общей полезности по x: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|||||||||||||
|
|
(TU |
|
) 12y |
|
|
|
(x |
|
|
) 12 |
2 |
|
y |
|
|
x |
|
|
8y |
|
|
x |
|
. |
|||||||||||||||||||||||
MU |
x |
x |
3 |
3 |
3 |
3 |
3 |
3 |
||||||||||||||||||||||||||||||||||||||||
3 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рассчитаем предельную полезность товара y. Для этого возьмем |
||||||||||||||||||||||||||||||||||||||||||||||||
частную производную функции общей полезности по y: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
2 |
|
2 |
|
|
||||||||||||||||||
|
|
|
|
) 12( y |
|
) x |
|
|
|
|
1 |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
MU |
y |
(TU |
y |
3 |
3 |
|
12 |
3 |
x 3 4 y |
3 |
|
x 3 . |
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Составим уравнение равновесия потребителя: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
MU y |
|
MU |
|
|
|
|
|
|
|
3 x 3 |
|
|
8y 3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
x |
|
4 y |
|
|
|
|
x |
|
|
; x 3y . |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
py |
|
px |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Подставим значение x в уравнение бюджетной линии и определим y:
54 2x 3y ; 54 2 3y 3y ; y 6 .
Подставим значение y в уравнение бюджетной линии и определим x:
54 2x 3 6 ; x 18.
Задача 2. Функция полезности потребителя имеет вид U = 0,25 xy. Доход потребителя составляет 400 руб. Цена товара x 40 руб. за единицу товара, цена товара y составляет 80 руб. Рассчитайте эффект замены и эффект дохода по Хиксу, если цена товара y снизится до 50 руб. за единицу товара.
Решение.
Так как функция полезности потребителя представляет собой функцию Кобба – Дугласа, то для расчета первоначальной точки опти-
28

мума потребителя (xn, yn) справедливо воспользоваться «методом долей
дохода»: x |
|
α I |
; y |
β |
|
I |
. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
α |
β P |
|
α β P |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
y |
|
|
|
|
|
|
|
Подставив |
исходные |
данные, получаем: |
x |
1 |
|
400 |
5; |
|||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
п |
2 |
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y |
1 |
|
400 |
2,5. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
п |
2 |
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, потребитель первоначально потреблял 5 ед. товара x и 2,5 ед. товара y, совокупная полезность первоначального набора составляла: Uп 0,25 5 2,5 3,125 ютилей.
Аналогично рассчитаем конечную точку оптимума (xк, yк) потреби-
теля после снижения цены на товар y до 50 руб. (Py2): |
x |
1 |
|
400 |
5; |
||||
|
|
||||||||
|
|
|
|
|
к |
2 |
40 |
|
|
|
|
|
|
|
|
|
|||
y |
1 |
|
400 |
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
к |
2 |
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для того чтобы рассчитать эффект дохода и эффект замены по методу Хикса, необходимо определить координаты вспомогательной точки (касание вспомогательного бюджетного ограничения, которое параллельно новому бюджетному ограничению и первоначальной кривой безразличия). Для этого необходимо решить систему уравнений:
1)Uв 3,125 0,25xв yв;
2)MUxв Px . MUyв Py2
Подставляем имеющиеся данные:
U |
|
0,25x y |
3,125 0,25x y |
xв 4 |
|
||||||||
|
в |
|
|
в в |
|
0,25y |
|
в в |
. |
||||
MUx |
|
Px |
|
40 |
|
||||||||
|
|
|
в |
|
|
|
|
в |
|
|
|
yв 3,2 |
|
|
|
|
Py2 |
|
50 |
|
|
||||||
MUyв |
|
|
0,25xв |
|
|
|
|||||||
Таким образом, эффект замены составляет ( yзамены yв yп ): yзамены 3,2 2,5 0,7 ед. товара.
Эффект дохода составляет ( yдохода yк yв ): yдохода 4 3,2 0,8 ед. товара.
29
Задания для самостоятельной работы
Графические упражнения
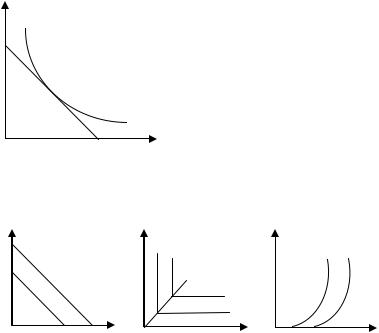
1. На рис.3.5 представлены линия бюджетного ограничения и кривая безразличия потребителя, который распределяет свой бюджет меж-
Qо |
|
|
|
|
|
ду покупкой обуви Qо |
и книг Qк. |
|
|
|
|
|
|
Укажите на рисунке точки, кото- |
|||
|
|
|
|
|
|
|||
D |
|
|
|
|
|
рые соответствуют |
следующим |
|
|
|
|
|
|
||||
|
|
B |
|
|
условиям: |
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
потребитель покупает только |
|
|
|
|
|
|
|
|||
|
|
A |
|
книги; |
|
|
||
|
|
|
|
потребитель не |
израсходо- |
|||
|
E |
|
|
вал весь бюджет; |
|
|||
|
|
|
|
|
|
|
набор, выходящий за преде- |
|
|
|
|
|
|
|
|||
|
|
|
|
C |
Qк |
лы бюджетных возможностей; |
||
|
|
|
|
|
точка оптимума потребителя. |
|||
|
Рис.3.5. К заданию 1 |
|
||||||
|
|
2. |
Определите, к какому типу |
|||||
|
|
|
|
|
|
|||
блага потребитель относит товар x для каждого из представленных на рис.3.6 вариантов, описывающих потребительские предпочтения:
QY |
QY |
U1 |
U2 |
QY |
U2 |
U1 |
|
|
|
||||
|
|
|
|
|
U1 U2
QX |
QX |
QX |
а |
б |
в |
|
Рис.3.6. К заданию 2 |
|
3. Опишите вкусы потребителя, если кривые безразличия имеют вид (рис.3.7).
30
