ОГЛАВЛЕНИЕ
1 Определение операторной передаточной функции ...........................................	4
2 Построение и анализ амплитудно-частотной и фазочастотной характеристик..............................................................................................................	6
3 Расчёт переходного процесса при заданном воздействии методом переменных состояния ............................................................................................	8
Список использованных источников .....................................................................	10
Приложение А ..........................................................................................................	11
Приложение В ...........................................................................................................	12

1 ОПРЕДЕЛЕНИЕ ОПЕРАТОРНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ

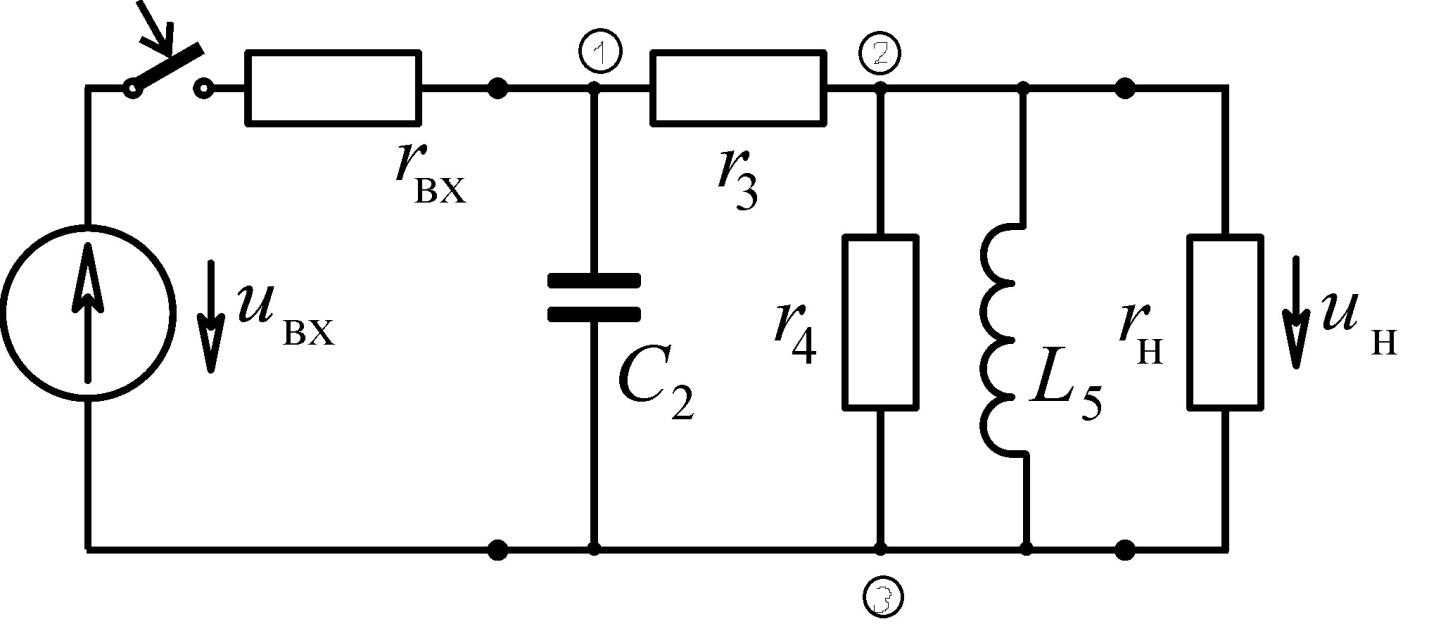
Топология схемы позволяет решить задачу путём последовательного сворачивания цепи

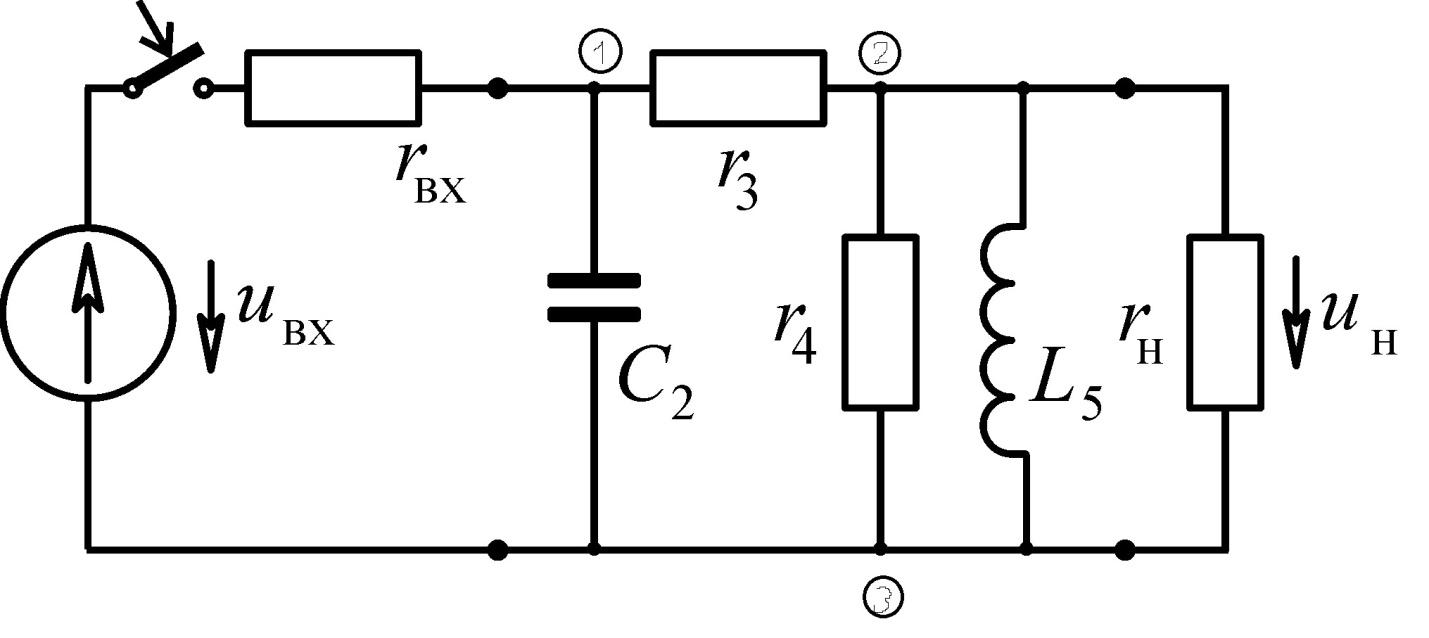
Рисунок 1- Схема электрической цепи

Выразим общее комплексное сопротивление цепи в операторной форме.

Комплексное сопротивление параллельного участка 5н:

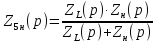(1)

Комплексное сопротивление параллельного участка 45н:

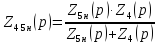(2)

Комплексное сопротивление последовательного участка 345н:

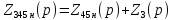(3)

Комплексное сопротивление параллельного участка 2345н:

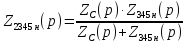(4)

Комплексное сопротивление всей цепи:

Z(p)=Z_вх(p)+Z_2345н(p) (5)

Передаточная функция:

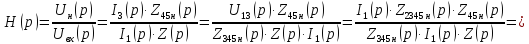
(6)

p=jω (7)

Все вычисления и упрощения сделаны в MathCAD 14, и приведены в приложении А.

2 ПОСТРОЕНИЕ И АНАЛИЗ АМПЛИТУДНО-ЧАСТОТНОЙ И ФАЗОЧАСТОТНОЙ ХАРАКТЕРИСТИК

Из лекционного курса известно, что амплитудно-частотная характеристика (АЧХ) цепи есть модуль комплексной передаточной функции:

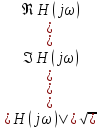(8)

Фазочастотная характеристика (ФЧХ) цепи – это аргумент комплексной передаточной функции 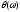, определяемый по формуле:

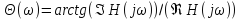(9)

Графики АЧХ и ФЧХ представлены ниже

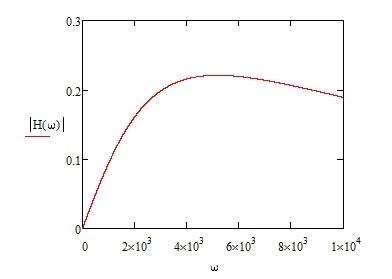
Рисунок 2 – Амплитудно-частотная характеристика

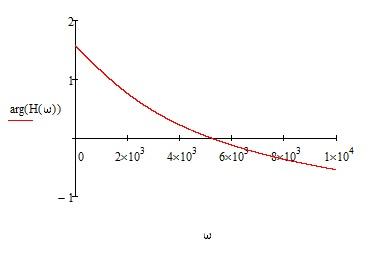
Рисунок 3- Фазочастотная характеристика

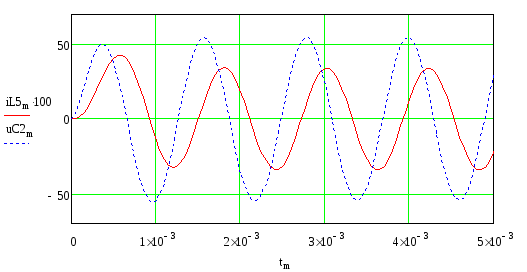
ω=5300 1/c - это резонансная частота контура L₅-C₂.

3 РАСЧЁТ ПЕРЕХОДНОГО ПРОЦЕССА ПРИ ЗАДАННОМ ВОЗДЕЙСТВИИ МЕТОДОМ ПЕРЕМЕННЫХ СОСТОЯНИЙ

На рисунке 4 представлена схема цепи с обозначением контуров и узлов.

Рисунок 4 – Схема цепи

Используя законы Кирхгофа составим систему уравнений:

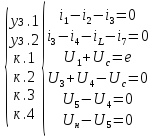, (10)

где ;

.

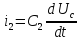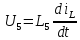Переменные состояния: i_L, U_C

После преобразований, окончательная запись системы для переменных состояния выглядит так:

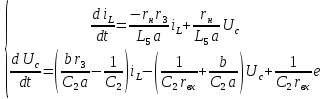, (11)

где ,

.

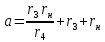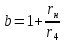Решаем полученную систему в среде MathCAD 14, там же строим графики переходного процесса. Подробное решение приведено в приложении B.

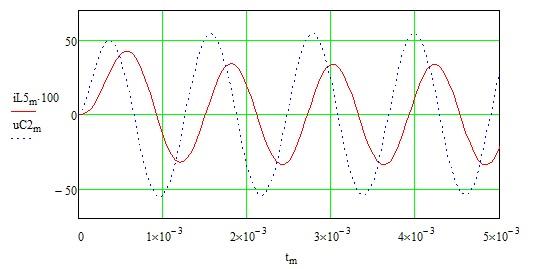
Рисунок 5 – График переходного процесса

На графике сплошной линией показано изменение тока на катушке индуктивности после замыкания ключа в цепи, а пунктирной линией показано изменение напряжения на конденсаторе.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1 Теория линейных электрических цепей: учебное пособие / В.В. Апанасов, Г.А. Баланцев. – Архангельск: Архан. гос. техн. ун-т, 2008. – 60 с.

ПРИЛОЖЕНИЕ А

Определение операторной передаточной функции

ПРИЛОЖЕНИЕ В

Расчет переходного процесса

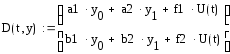
3