LR_Istechenie_vozdukha

Удельный объем воздуха перед соплом

, (40)

в выходном сечении сопла при изоэнтропийном расширении

, (41)

Правильность определения термических параметров состояния на выходе проверяется исходя из необходимости выполнения условия

, (42)

Теоретическая скорость истечения вычисляется по формуле (12), критическая скорость вычисляется по формуле

, (43)

где - критическое значение энтальпии, определяется по таблицам С.Л. Ривкина

при Т = Т_кр (см. формулу 18).

Далее вновь рассчитывают скоростной коэффициент сопла . По­тери энергии на трение и действительное значение энтальпии воздуха в выходном сечении сопла определяют по зависимостям (29), (30). Используя таблицы, по значениям и находят. Зная , по уравнению неразрывности легко най­ти G, а затем и безразмерные .

При выполнении работы необходимо проанализировать зависимость коэффициента расхода от числа Рейнольдса

, (44)

где - коэффициент динамической вязкости воздуха,

,

- плотность воздуха в выходном сечении,

В координатах T S (рисунок 7) в масштабе строят процессы адиабат­ного расширения воздуха в суживающемся сопле: теоретический изоэнтропийный и условный необратимый. Необходимое для построения значение приращения энтропии за счет необрати­мости рассчитывают по формуле (31). Величина потерь энергии, как видно из рисунка 7, может быть представлена графи­чески в виде площади криволинейной трапеции. Спрямив участок изобары Р₂ между точками 2 и 2g, приближенно мож­но записать:

. (45)

Полученное значение сравнивают с вычисленным по форму­ле (29).

Рисунок 7 Теоретический и дей-ствительный процессы рас­ширения воздуха в сопле

Анализ полученных результатов

После обработки опытных данных результаты исследований пред­ставляют графически в виде зависимостей , устанавливают критическое отношение дав­лений. Из сравнения экспериментальных распределений с рас­четными делают вывод о степени приближения реального течения к теоретической модели, рассмотренной выше. Среднеквадратичные отклоне­ния опытных точек от аналитических зависимостей (30), (39) рассчиты­вают по формулам

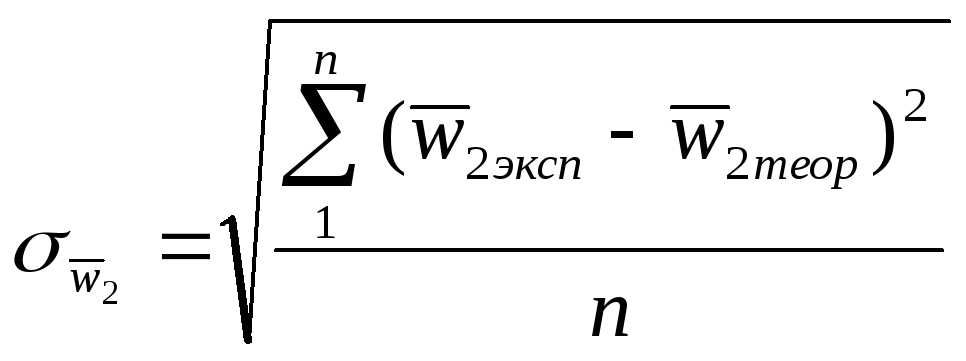, (46)

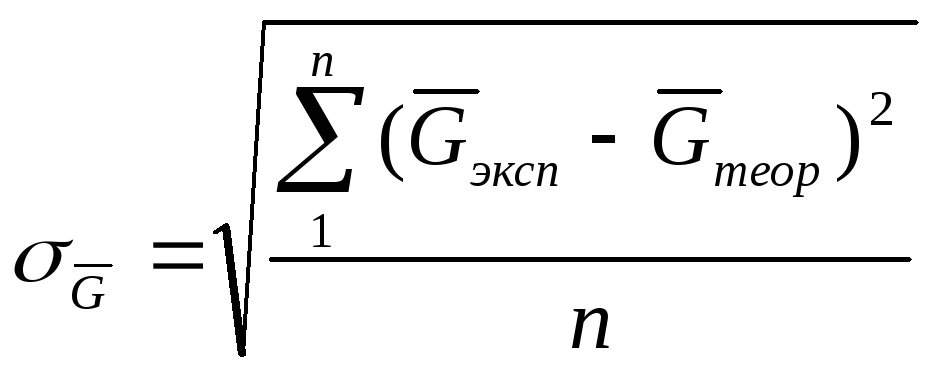. (47)

Расчет погрешностей измерений

Предельная относительная погрешность (ошибка) отдельного из­мерения (серии измерений) определяется как отношение максимальной абсолютной погрешности к абсолютному значению (среднеарифметичес­кому значению) измеряемой величины, то есть

.

Этой же зависимостью можно пользоваться и при функциональной свя­зи искомой величин . Здесь - параметры. Однако для преобразования выражения (48) в расчетную формулу необходимо знать математическое описание функции .

Предельная относительная погрешность определения плотности:

, (49)

Предельная относительная ошибка определения массового расхода

, (50)

где - относительная ошибка определения , по данным тарировки

сопла = 0,01.

Предельная относительная погрешность определения скорости ис­течения вычисляется по формуле

, (51)

При выполнении расчетов по формулам (49) - (51) предполагается, что абсолютные предельные погрешности измерений приборов принимают­ся равными половине наименьшей цены деления шкалы, = 0,01 мм.

Отчет по работе

Отчет должен содержать:

1) формулировку цели исследования;

2) схему и описание экспериментальной установки;

3) результаты измерений и расчетов, представленные в таблич­ной форме;

4) графический иллюстративный материал;

5) расчет погрешности измерений;

6) краткие выводы по работе;

7) ответы на контрольные вопросы;

8) список использованной литературы.

Контрольные вопросы

1. Что называется процессом истечения?

2. Перечислите внешние воздействия, вызывающие изменение ско­рости потока; запишите дифференциальное уравнение продольного про­филя канала.

З. В чем состоит сущность гипотезы Сен-Венана-Вантцеля?

4. Объясните физический смысл коэффициентов и .

5. Можно ли и при каких условиях в суживающемся сопле получить сверхзвуковую скорость? Объясните физический смысл числа Маха.

6. Запишите уравнение первого закона термодинамики для потока.

7. Какие факторы оказывают влияние на величину скоростного коэффициента сопла?

____________________________________________

Знак " ~ " (тильда) над величиной означает, что последняя рассматривается как среднеарифметическая.