LR_Istechenie_vozdukha

ЛАБОРАТОРНАЯ РАБОТА №1

ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЕ

АДИАБАТНОГО ИСТЕЧЕНИЯ ВОЗДУХА ЧЕРЕЗ СУЖИВАЮЩЕЕСЯ СОПЛО

Цель работы – углубление и закрепление знаний по курсам технической термодинамики (раздел «Термодинамика потока») и гидродинамики (раздел «Одномерное движение газа»), изучение методики экспериментального исследования истечения газа через суживающееся сопло, определение расходных и скоростных характеристик при различных режимах вплоть до критического, получение навыков в проведении расчётов насадков с использованием таблиц термодинамических свойств газов, оценки степени достоверности результатов и погрешностей измерений.

Основные теоретические положения

Задачами расчёта процесса истечения являются определение скорости и параметров состояния в характерных сечениях канала, выявление его продольного профиля и размеров (при заданном расходе среды): площади (диаметра) сопла в минимальном и выходном сечениях, длины расширяющейся части (для сопел Лаваля).

При термогазодинамеческом анализе одномерного течения рабочего тела в каналах и расчёте насадков используется два основных уравнения: первого закона термодинамики (сохранения энергии) и неразрывности (сплошности).

Для открытых (поточных) систем уравнение первого закона термодинамики удобно представить в следующей дифференциальной форме:

(1)

уравнение неразрывности имеет вид

, (2)

или в дифференциальной форме

, (3)

где удельный объем;

Р – давление;

 – средняя скорость потока;

q – ускорение свободного падения, g = 9,80665 м/с²;

z – высота расположения центра тяжести рассматриваемого сечения потока

относительно выбранной плоскости сравнения;

l_техн – техническая работа, подводимая или отводимая от потока (в

компрессорах, насосах, вентиляторах, паровых и газовых турбинах,

МГД-каналах и т.д.)

l_тр – работа сил трения;

G – массовый расход;

f – площадь поперечного сечения потока (канала).

Выражение, стоящее в правой части уравнения ( I ), представляет собой бесконечно малое приращение располагаемой (внешней полезной) работы движущегося рабочего тела. Таким образом, располагаемая работа в потоке, затрачиваемая на изменение его внешней кинетической и потенциальной энергий, на совершение технической работы и преодоление сил трения.

Условия, обеспечивающие изменение скорости течения вдоль оси канала при наложении на поток внешних воздействий, описываются в общем виде законом обращения воздействий:

,

где М – число Маха, ;

q_внешн – внешняя теплота процесса;

q_тр – теплота трения.

Выражение (4) является математической записью закона обращения воздействий, впервые сформулированного известным советским теплофизиком Л.А. Вулисом, [2]: любым внешним воздействием (геометрическое, расходное, тепловое, механическое и т.д.) можно вызвать изменение скорости потока (ускорение или торможение), однако, для непрерывного перехода через скорость звука необходимо обратить воздействие, то есть изменить его знак на противоположный.

Уравнение (4) несколько упрощается, если в качестве рабочего тела рассматривать газ, близкий по свойствам к идеальному (совершенному) и удовлетворяющий уравнению Клайперона.

. (5)

Для этого случая:

, ;

и

(6)

С учетом выражения (6) уравнение закона обращения воздействий можно записать следующим образом:

(7)

Л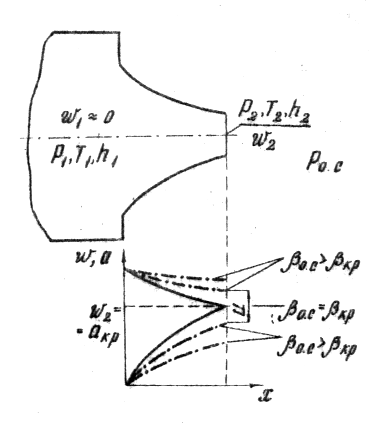егко видеть, что каждое слагаемое в правой части уравнений (4) и (7) отражает определенный вид воздействия на поток. Наиболее простой и характерный для теплоэнергетических установок теоретический случай адиабатного изоэнтропийного течения реализуется при отсутствии всех воздействий, кроме геометрического: dq_внешн = 0,

dl_техн = 0, dl_тр = dq_тр = 0 и dz = 0.

При этом соотношение (7) переходит в уравнение Гюгонио:

, (8)

или

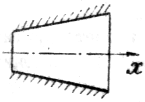
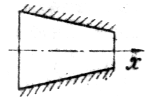
Рисунок 1 Схематический чертеж сужа-ющегося сопла и изменение скорости звука и потока газа по длине его проточной части

, (9)

где х – продольная координата.

Соотношение (9), называемое иначе уравнением продольного профиля канала, позволяет проанализировать влияние геометрического воздействия (закон изменения площади поперечного сечения по длине канала) на изменение скорости потока в условиях дозвукового и сверхзвукового течений (таблица 1). Как видно из таблицы 1, при истечении рабочего тела через суживающийся насадок в дозвуковом режиме его скорость по длине сопла возрастает. Для адиабатного течения скорость потока на выходе из сопла (рисунок 1) может быть найдена при интегрировании уравнения ( I ):

,

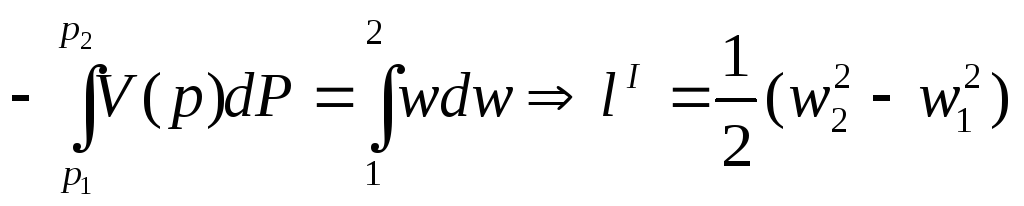или

,

где l^I – удельная располагаемая работа адиабатного процесса, Дж/кг;

h₁, h₂ – начальная и конечная энтальпия рабочего тела, Дж/кг.

Во многих случаях начальная скорость течения , поэтому:

, (11)

или

, (12)

Здесь h выражено в килоджоулях на килограмм.

Формулы (10) – (12) являются универсальными, т.к. справедливы как для идеальных, так и для реальных газов.

Таблица 1

Характер воздействия	Дозвуковой поток (М<1)	Сверхзвуковой поток (М>1)
Ускорение потока

При адиабатном обратимом истечении совершенного газа расчетная зависимость (II) может быть преобразована к виду:

, (13)

где - отношение давлений, .

Массовый расход газа в выходном сечении сопла легко определяется из уравнения неразрывности (2):

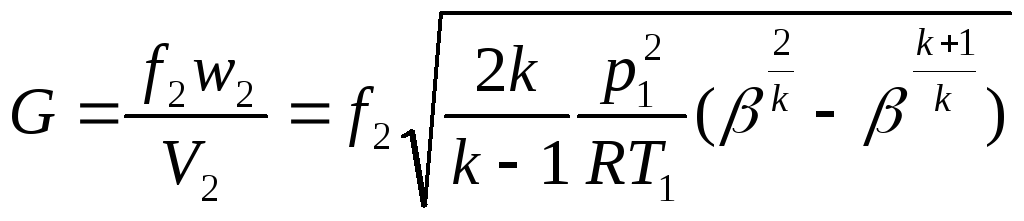, (14)

Из анализа формулы (14) следует, что G = 0 при = 0 и = 1. При 0<<1 расход всегда больше нуля. Следовательно, должно существовать определенное (критическое) значение , при котором массовый расход газа достигает максимального значения. Последнее устанавливается из условия экстремума функции G = G():

, (15)

Выполнив операцию дифференцирования, получаем:

, (16)

Для двухатомных газов (k = 1,4), в том числе и воздуха . В конце адиабатного расширения давление Р₂, при котором достигается максимальный расход G_max, называют критическим:

, (17)

Критические значения T и легко выразить через начальные параметры состояния, воспользовавшись известными соотношениями между термическими параметрами в адиабатном процессе:

, (18)

, (19)

Запишем формулы для расчета критических значений и G, подставив в выражения (13) и (14) значение по зависимости (16). Отсюда:

, (20)

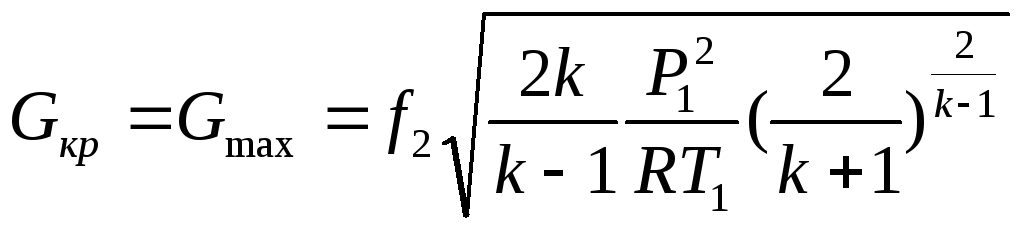, (21)

Подставив в формулу (20) значение Т₁ по формуле (18), свяжем w_кр с критическими параметрами состояний:

, (22)

Рисунок 2 Зависимость дав-ления в выходном сечении суживающегося сопла от ве-личины

Таким образом, при достижении критического состояния в выходном сечении суживающегося сопла скорость истечения становится равной местной скорости звука.

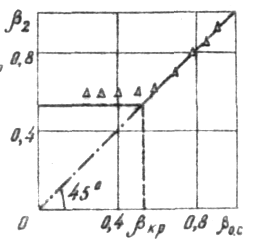
Как показывает эксперимент (рисунок 2), при уменьшении давления окружающей среды Р_ас, в которую происходит истечение, пропорцио­нально уменьшается и давление в выходном отверстии насадка вплоть до Р_кр. При Р_ас < Р_кр () не меняется. Теоретические зависимости изменения безразмерных скорости и расхода от также зна­чительно расходятся с опытными данны­ми (рисунок 3 и 4).

С физической точки зрения данное явление объясняется следующим образом. Изменение (уменьшение) Р_ас не вызывает в среде малые возмущения, распространяю­щиеся, как известно из физики, со ско­ростью звука. При скорости истечения w₂ < a возмущения проникают в проточную часть сопла и распространяются вдоль оси к входному сече­нию с относительной скоростью u = а - V (см. рисунок 1), вызывая соответствующее перераспределение кинематических параметров потока.

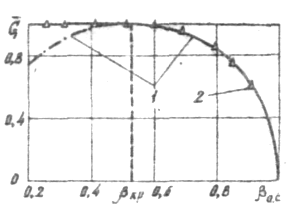
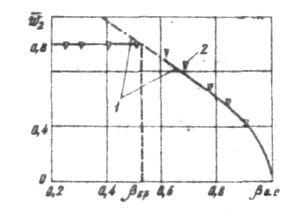
Рисунок 3 Зависимость безразмерного массового расхода газа от величины 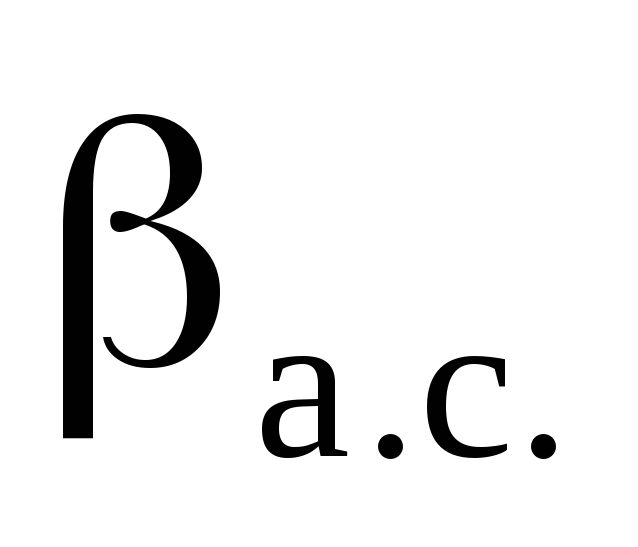: 1 – кривая, рассчитываемая по уравнению (38); 2 – опытные точки

Рисунок 4 Влияние 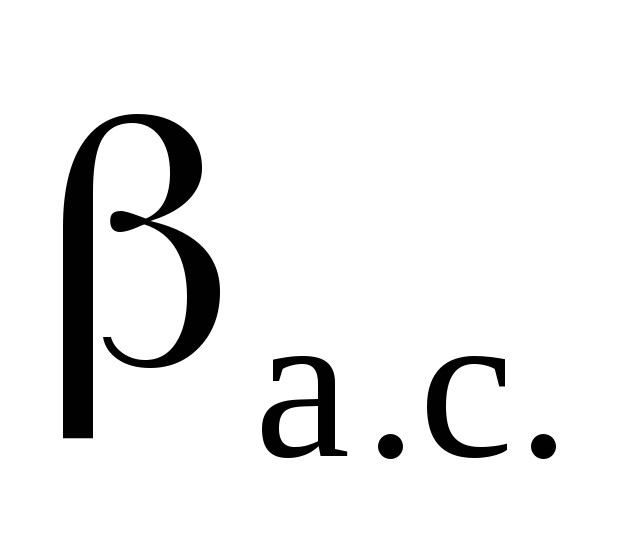на величину безразмерной скорости газа в выходном сечении сопла: 1 – кривая, рассчитываемая по уравнению (39); 2 – опытные точки

При выполнении условия , и . Следовательно, при дальнейшем снижении Р_а.с. внешние возмущения уже не могут оказать воздействия на течение, как бы сносятся им. В этом случае говорят, что сопло является "запертым", то есть изо­лированным от влияния окружающей среды (противодавления).

Точность теоретических расчетов сопел можно повысить, если учесть нелинейную зависимость теплоемкостей Ср и Сv , а следова­тельно, и показателя адиабаты k от температуры. В современных вы­сокотемпературных газотурбинных установках начальная температура рабочего тела составляет 900 ... 1200 ⁰С, поэтому использование в рас­четах формул (21), (22) и др. при k = const может привести к существенным погрешностям.

В этом случае целесообразно использовать таблицы термодинами­ческих свойств газов, например таблицы, составленные С.Л.Ривкиным по данным ВТИ [6]. Таблицы позволяют производить о достаточной точ­ностью (допустимая погрешность не превышает 0,5% и большим удоб­ством расчеты изоэнтропийных процессов газов и газовых смесей в об­ласти давлений до 2,5...3,0 МПа и температур до 1500°С.

Приведенные в таблицах безразмерные параметры получены следую­щим образом. Дифференциальное уравнение изоэнтропийного процесса имеет вид

, (23)

Разделяя переменные и интегрируя уравнение (23) от некоторого вы­бранного нулевого состояния до заданного, получаем:

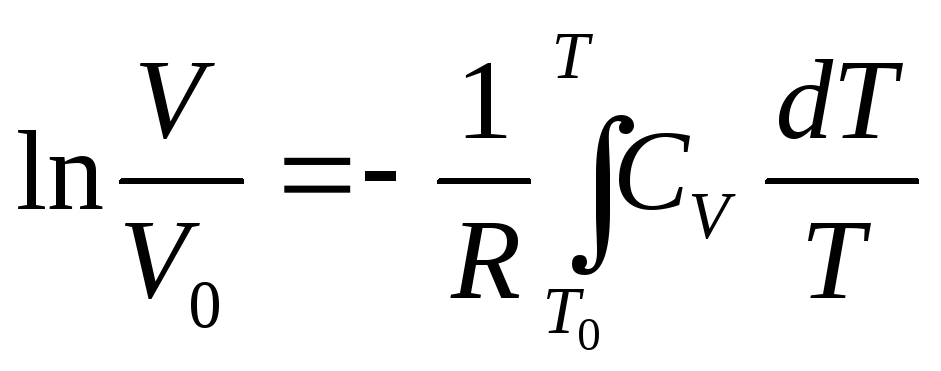, (24)

После потенцирования имеем

, (25)

где ;

- относительный удельный объем.

Аналогичным образом, рассматривая уравнение изоэнтропийного процесса в виде:

, (26)

можно получить соотношение

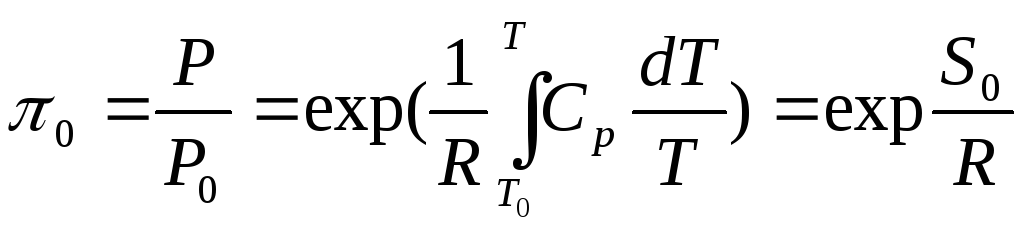(27)

где - относительное давление;

S₀ - функция температуры, имеющая смысл удельной энтропии изобарного

процесса, отсчитанной от нулевой температуры, ; T₀ = 0 K,

C_p = C_p(T).

Значения функций , , для различных газов просчитаны в интервале температур от –50 ... +1500 С и затабулированы. Кроме того, в таблицах приведены значения удельных эн­тальпии энтропии отсчитанные от 0 К.

Реальные процессы истечения не являются изоэнтропийными вслед­ствие необратимости, как внешней, так и внутренней. Внешняя необ­ратимость вызывается теплообменом рассматриваемой системы с окру­жающей средой. Однако при расчетах процессов истечения, характери­зующихся высокими скоростями перемещении рабочего тела, влияние теплообмена можно не учитывать. Значительно большее воздействие на течение оказывают трение газа о стенки канала, перестройка скорост­ного поля по тракту насадка и связанные с ней потери на вихреобразования. В итоге действительная скорость истечения w_2g всегда мень­ше теоретической. Последняя обычно, учитывается введением так назы­ваемого скоростного коэффициента сопла:

(28)

Величина зависит от технологии изготовления сопел, конфигурации, длины (высоты сопловых решеток в турбинах) и некоторых других фак­торов (рисунок 5). Большие значения соответствуют насадкам с плав­ной и тщательно обработанной (полированной) сходящейся частью.

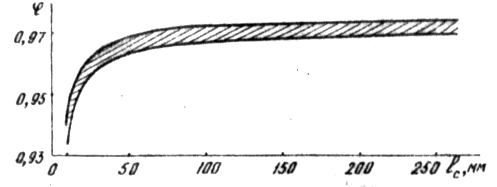
Рисунок 5 Зависимость скоростного коэффициента от длины (высоты) сопловых турбинных решеток

Разность энтальпий потока в начале и конце действительного процесса расширения (h₁ – h_2g) меньше теоретической (h₁ – h₂) на величину потерь энергии:

, (29)

где - коэффициент потерь энергии;

h - теплоперепад.

Это связано с тем, что работа сил трения в потоке необратимо переходит в теплоту трения, поэтому конечная энтальпия газа воз­растает :

, (30)

Приращение энтропии системы, вызванное необратимостью процесса ис­течения, можно определить, воспользовавшись таблицами С.Л. Ривкина:

(31)

Описание экспериментальной установки

и методики измерений

Экспериментальная часть лабораторных работ выполняется на стенде, схематический чертеж которого приведен на рисунке 6.Основным элементом стенда является суживающееся сопло 8 длиной l_c = 42 мм о диаметром выходгого отверстия d_c = 1,5 мм, установленное в участ­ке трубопровода 1. Экспериментальный участок через регулирующий кран 7 гибким шлангом соединяется с вакуум-насосом 6.

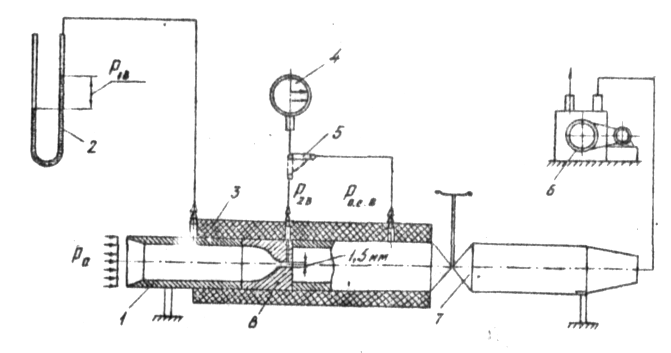
Рисунок 6 Схематический чертеж экспериментального стенда по

исследованию истечения воздуха через суживающееся сопло

При включенном насосе и открытом кране воздух, забираемый из помещений, просасывается через сопло и из выхлопного патрубка сбрасывается в окружающую среду.

Расход газа через насадок определяется степенью открытия регулирующего крана и измеряется косвенным путем по перепаду статичес­кого давления в сопле, предварительно протарированном с помощью газового счетчика.

В работе измеряются атмосферное давление воздуха Р_а и температура t₁ в помещении, вакуумметрические статические давления воздуха в трубопроводе перед соплом P_1В (с помощью дифференциаль­ного водяного манометра 2), в выходном отверстии сопла P_2В и за соплом Р_а.с. (с помощью манометра-вакуумметра 4 и пневмопереключателя 5).

Результаты измерений заносятся в таблицу 2.

Таблица 2

№ п/п

Ра

P1В

P2В

Ра.с.в

Gд

а.с

Для исключения (уменьшения) теплообмена с окружающей средой рабочая часть экспериментального участка трубопровода теплоизолиро­вана слоем поролона 3 .

Выполнение работы начинают с расчета минимальных расходов^* воздуха через сопло. Постепенно увеличивая степень открытия кра­на, достигают критического режима истечения. При докритическом режиме показания вакуумметра P_2В и Р_а.с.в практически одинаковы. При дальнейшем понижении Р_а.с.в и достижении критической величины значе­ние P_2В перестает зависеть от давлений за соплом. Величина записывается в таблицу 2 и используется при определении массового рас­хода воздуха.

Обработка результатов наблюдений

Плотность воздуха перед соплом рассчитывают по уравнению Клапейрона:

, (32)

Массовый расход воздуха через экспериментальный насадок опре­деляют методом переменного перепада давления:

, (33)

где - коэффициент пропорциональности, зависящий от относи­тельного перепада

давления в сопле и рассчитываемый по тарировочной зависимости.

, (34)

.

Действительную скорость истечения воздуха находят по уравне­нию неразрывности (2), оценивая удельный объем в конце процесса расширения по соотношению между Т и Р для изоэнтропийного про­цесса.

Таким образом,

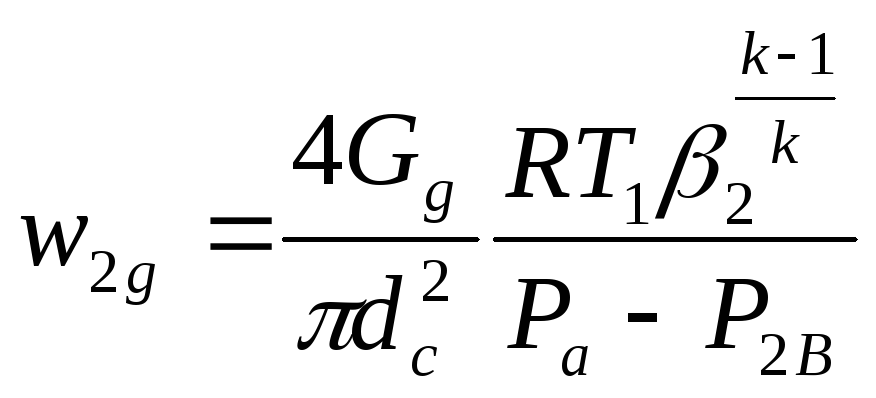, (35)

где .

Отношение давлений, определяемое внешними условиями,

, (36)

Теоретическая скорость истечения воздуха вычисляется по формуле (13). После этого легко определить скоростной коэффициент сопла по соотношению (28).

Массовый расход газа при изоэнтропийном истечении рассчиты­вают, используя зависимость (14).

_________________________________________

^*Общее число режимов принимается не менее 8.

Коэффициент расхода

, (37)

Безразмерный расчетный массовый расход воздуха через сопло опреде­ляется по формуле:

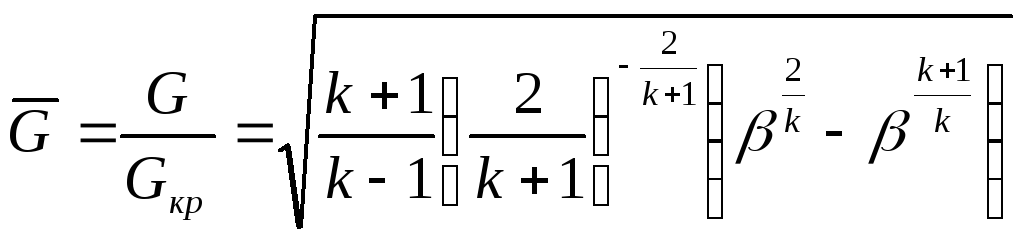, (38)

Безразмерная расчетная скорость газа в выходном сечении сопла

, (39)

Расчет процесса истечения по таблицам термодинамических свойств газов, частично приведенным в приложении, производят в сле­дующей последовательности. По начальной температуре воздуха находят значения и S_01. Так как , то относительное давление в конце процесса расширения . Зная , по таблицам С.Л. Ривкина интерполяцией легко установить значения Т₂, h₂, .