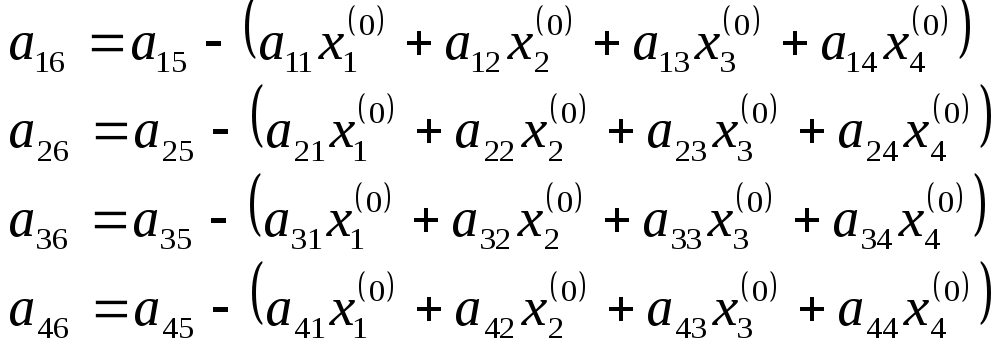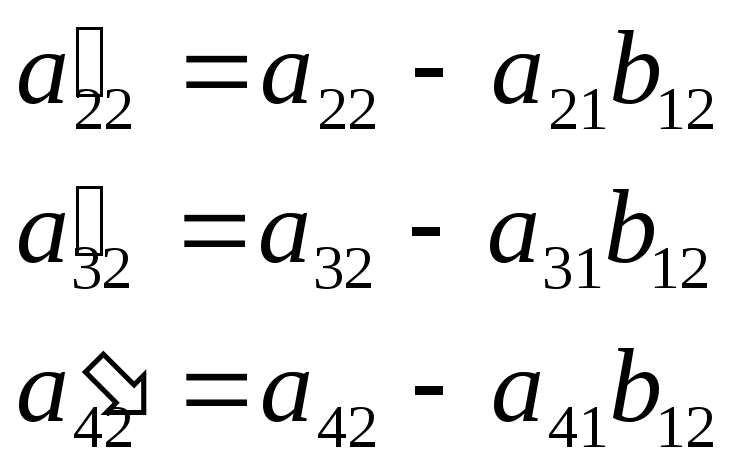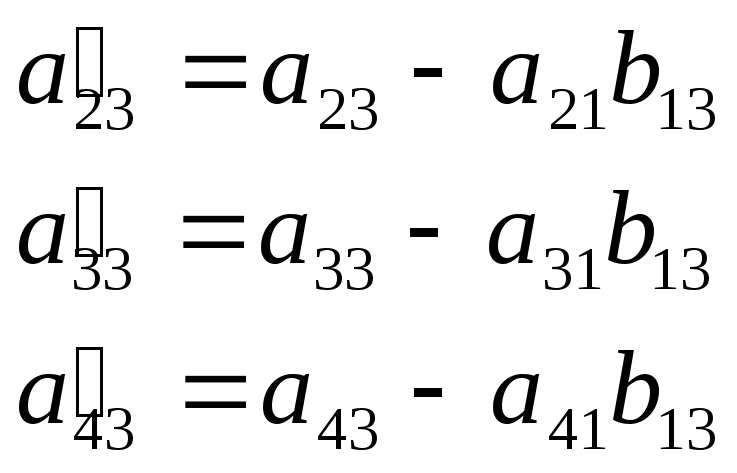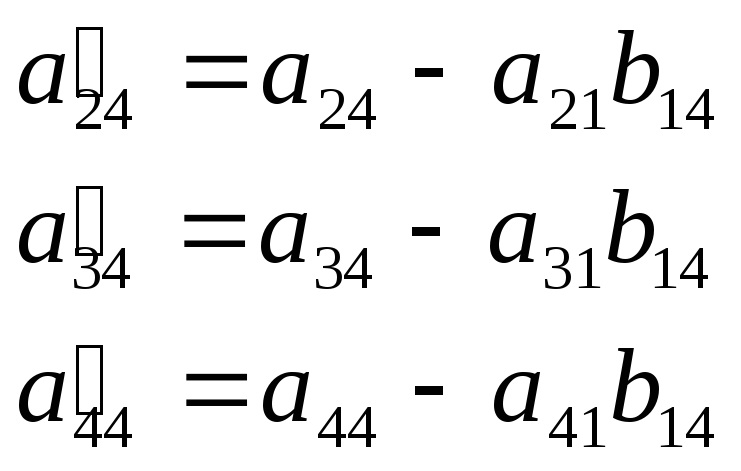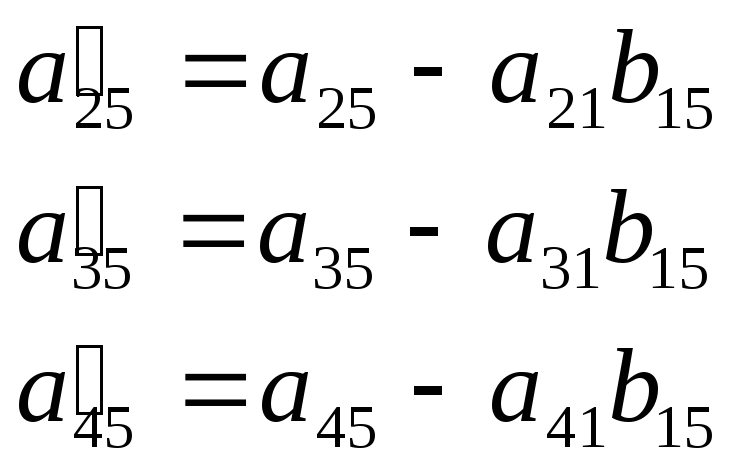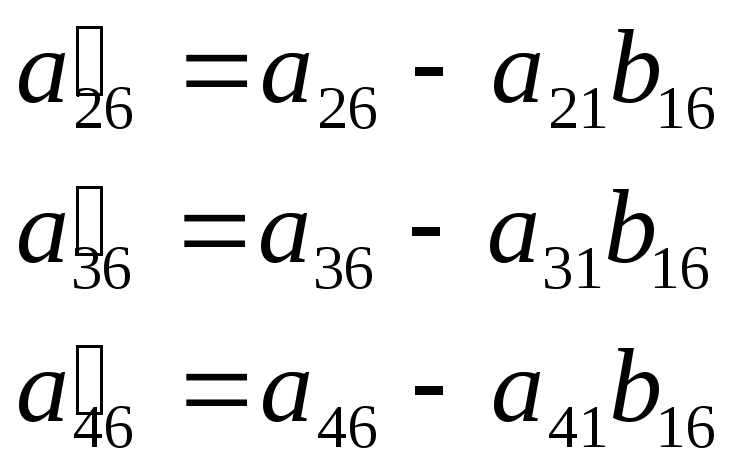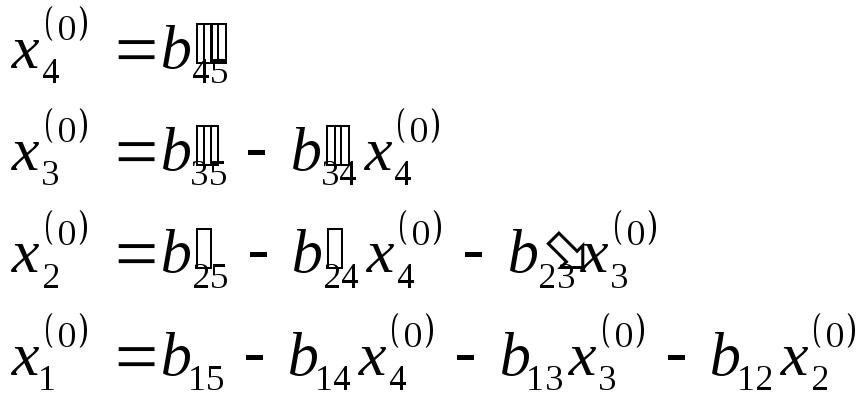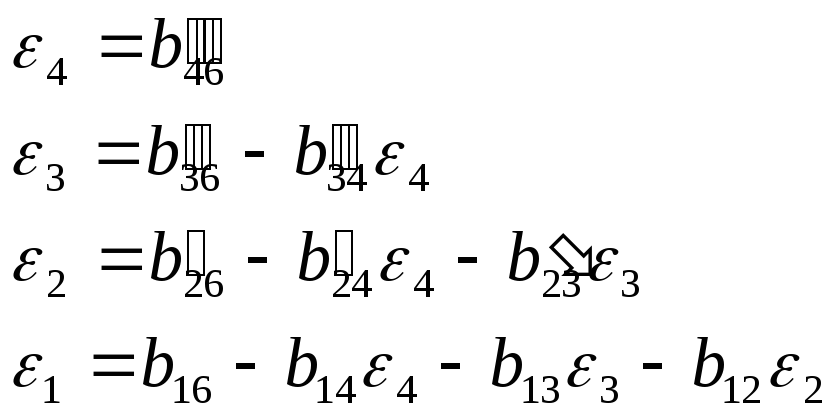- •Лабораторная работа №1 «Элементарная теория погрешностей»
- •Лабораторная работа №2 «Элементарная теория погрешностей»
- •Лабораторная работа №3 «Метод половинного деления»
- •Лабораторная работа №4: «Решение нелинейных уравнений методом хорд и касательных».
- •2)Метод касательных (Ньютона).
- •Лабораторная работа №5 «Комбинированный метод»
- •Лабораторная работа №6: «Решение нелинейных уравнений методом простой итерации».
- •Метод главных элементов для решения системы уравнений
- •Лабораторная работа №8 «Метод Гаусса»
- •Лабораторная работа №9 «Метод Халецкого»
- •Порядок заполнения таблицы:
- •Лабораторная работа №10 «Метод квадратных корней»
- •Лабораторная работа №11 «Метод итераций»
- •Лабораторная работа № 12 «Метод Зейделя»
- •Лабораторная работа13. Интерполирование функции многочленом Лагранжа.
- •Лабораторная работа14. Интерполирование функции многочленом Ньютона.
- •Лабораторная работа15. Сплайновая интерполяция.
- •Лабораторная работа16 Интерполяция функции кубическим сплайном. Метод прогонки.
- •Образец выполнения задания:
- •Лабораторная работа17 Среднеквадратическое приближение
- •Образец выполнения задания:
- •Лабораторная работа18 Ортогональные многочлены Чебышева
- •Образец выполнения задания:
- •Лабораторная работа19. Вычисление определенных интегралов по формуле трапеций и формуле Симпсона, по формуле левых, правых и средних прямоугольников.
- •3) Вычислить определенный интеграл по формуле левых и правых прямоугольников.
- •4) Вычислить определенный интеграл по формуле средних прямоугольников.
- •Лабораторная работа 20. Метод Эйлера с уточнением
- •Л/р 21«Численное решение ду первого порядка методом Рунге-Кутты 4-го порядка».
- •Л/р22 «Решение ду первого порядка методом Адамса-Башфорта».
- •Лабораторная работа 24
- •4. Минимизация функции f(X) методом барьерных функций:
Лабораторная работа №8 «Метод Гаусса»
Используя
схему Гаусса, решить систему уравнений
с точностью до ![]() .
.
1.
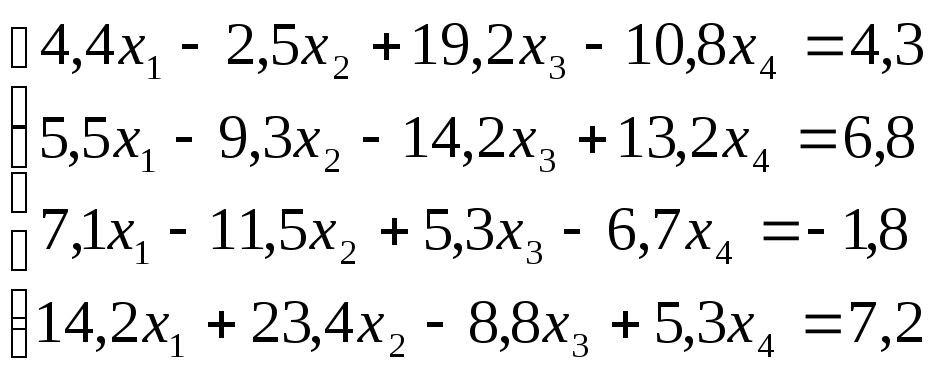 16.
16.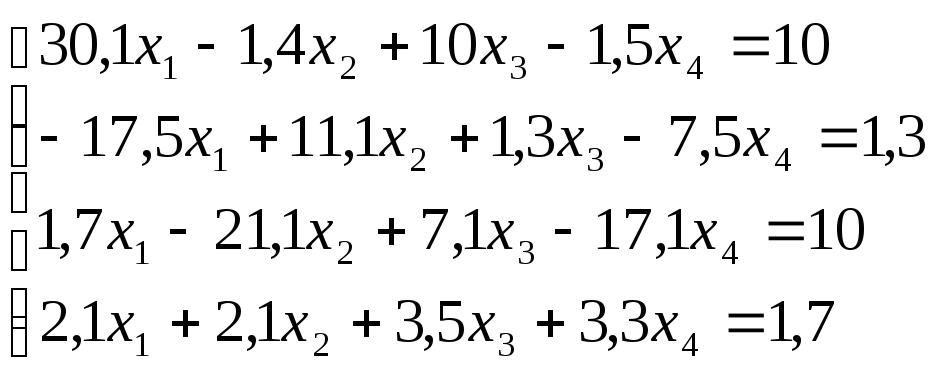
2.
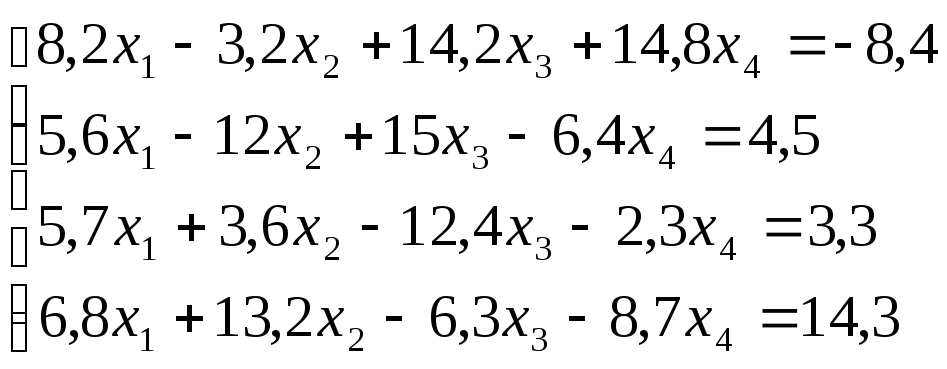 17.
17.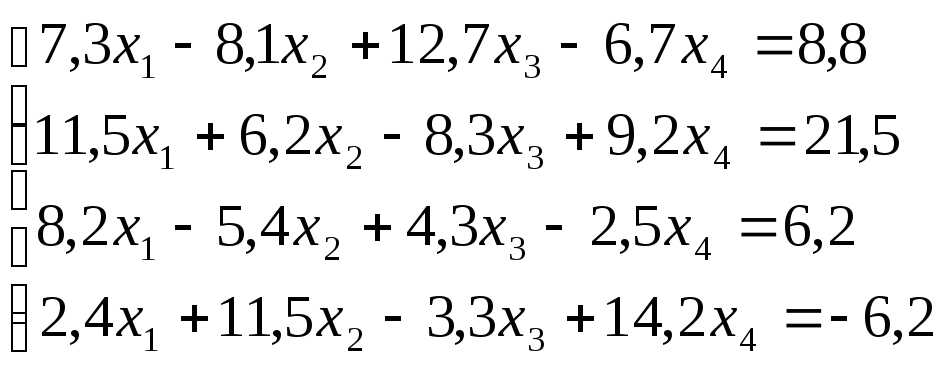
3.
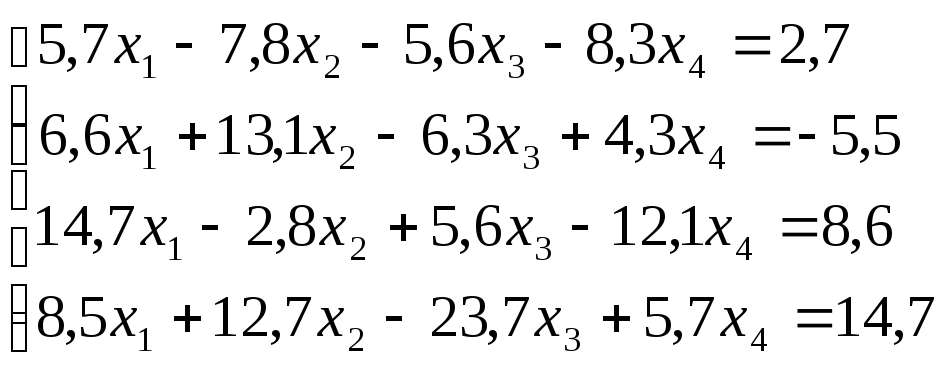 18.
18.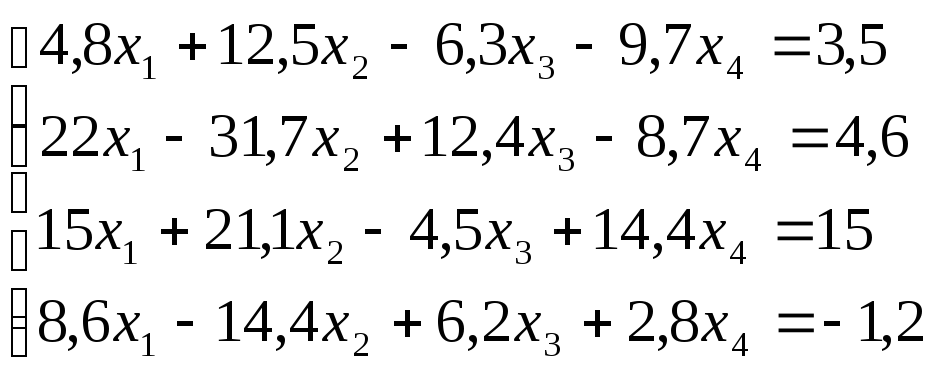
4.
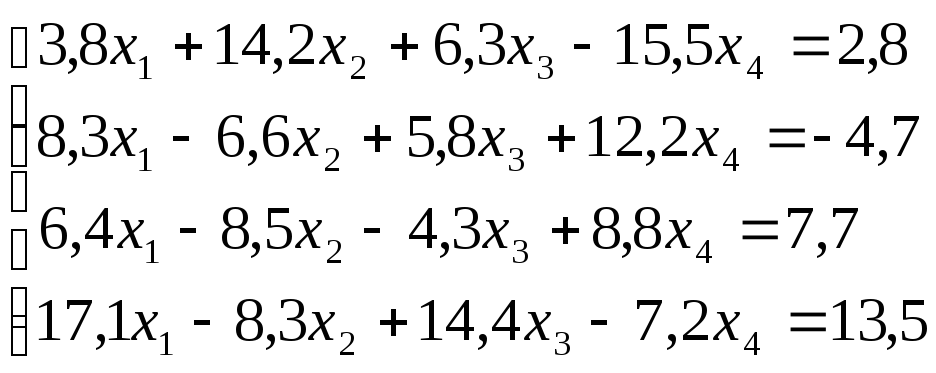 19.
19.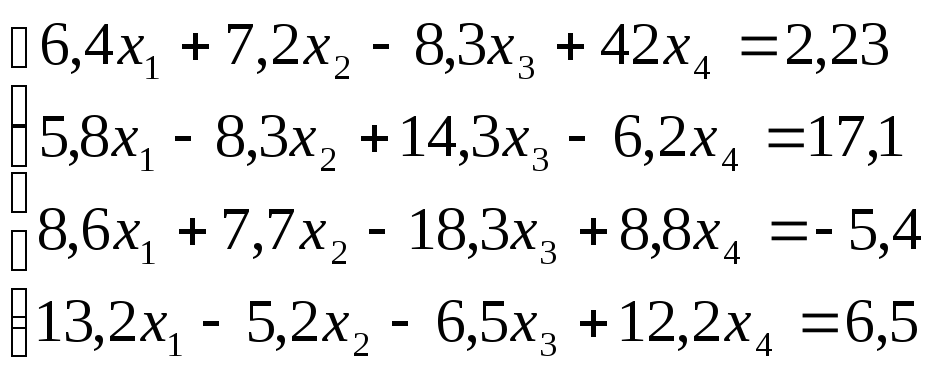
5.
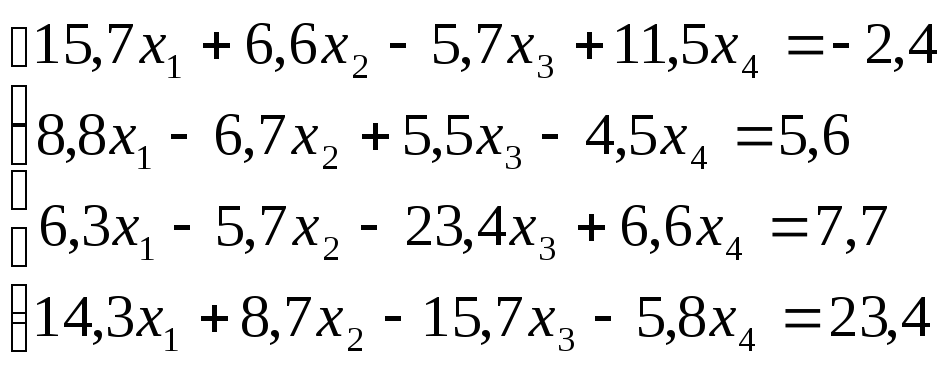 20.
20.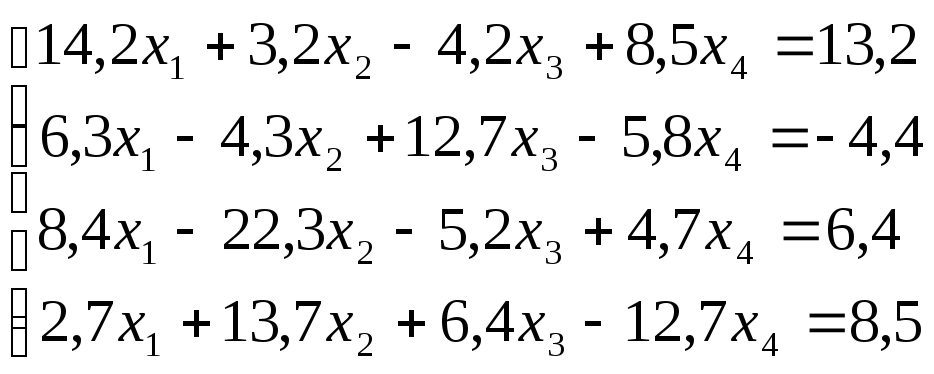
6.
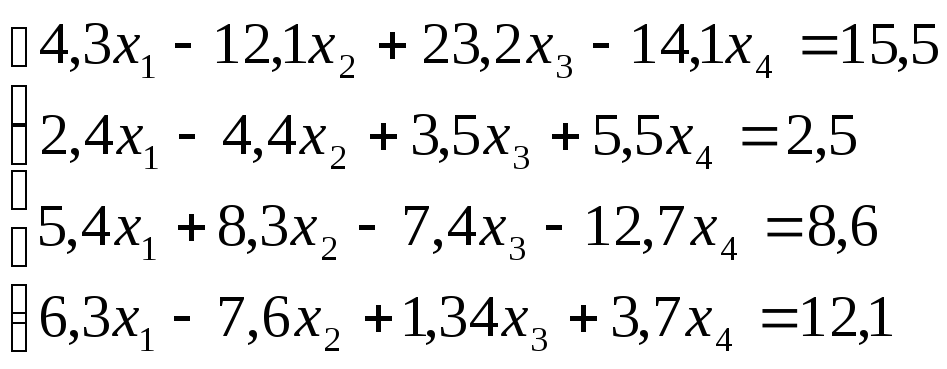 21.
21.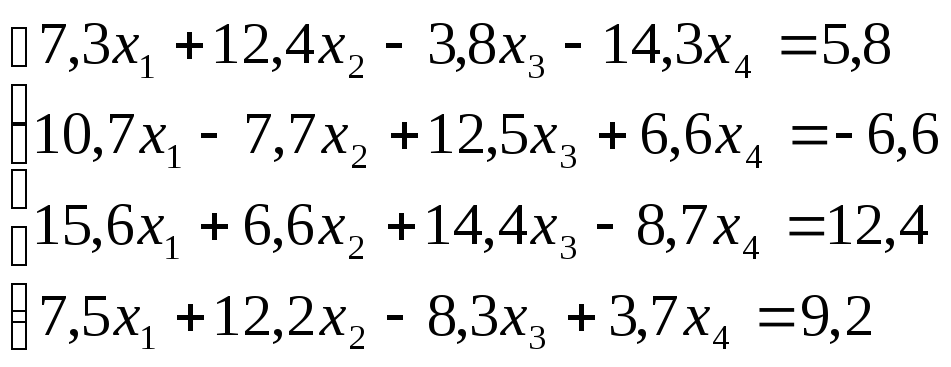
7.
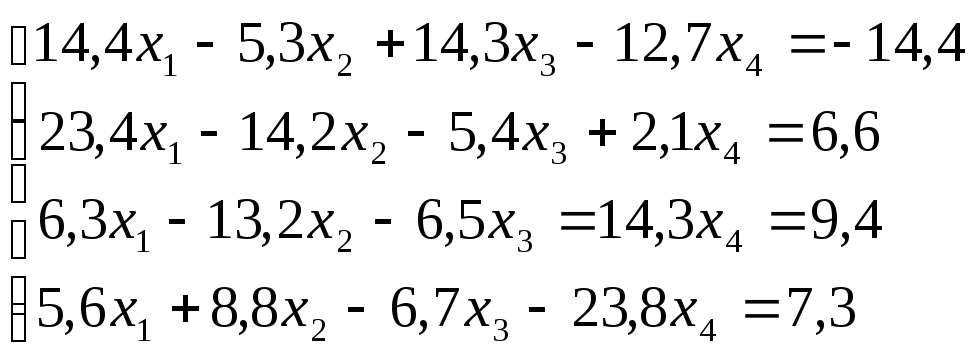 22.
22.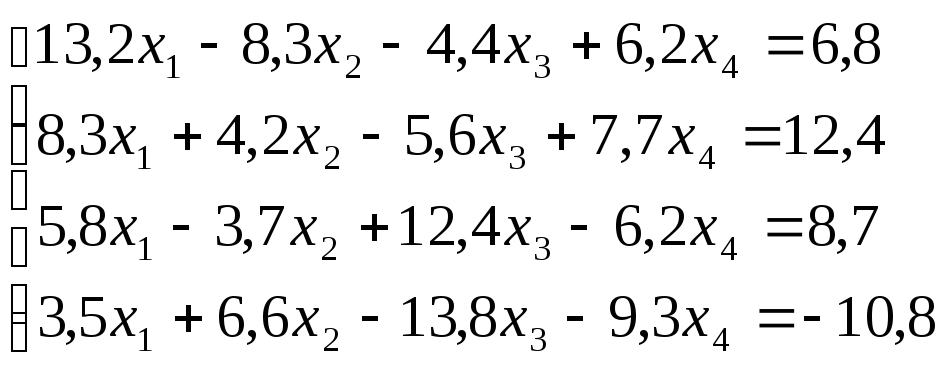
8.
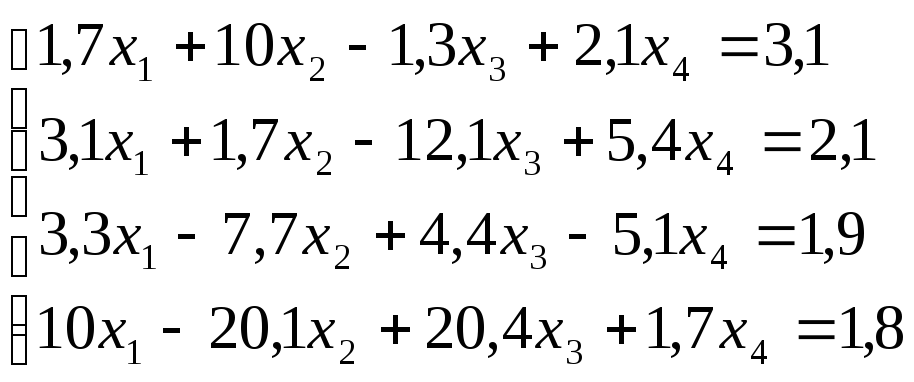 23.
23.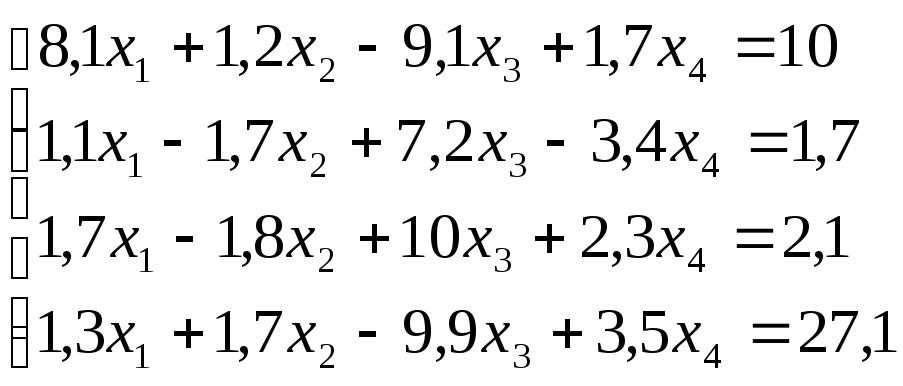
9.
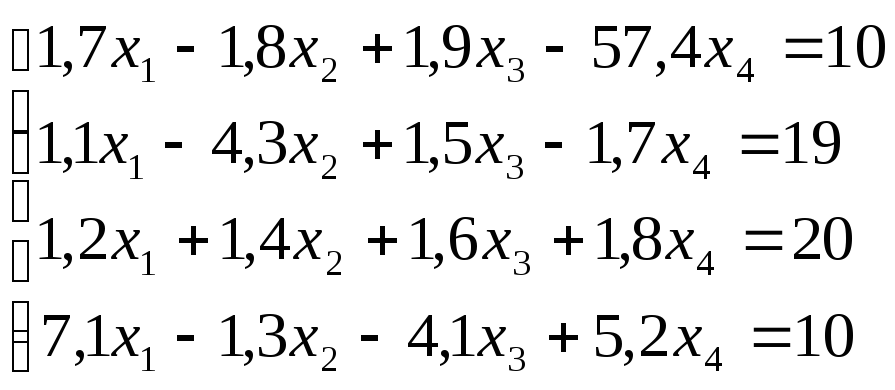 24.
24.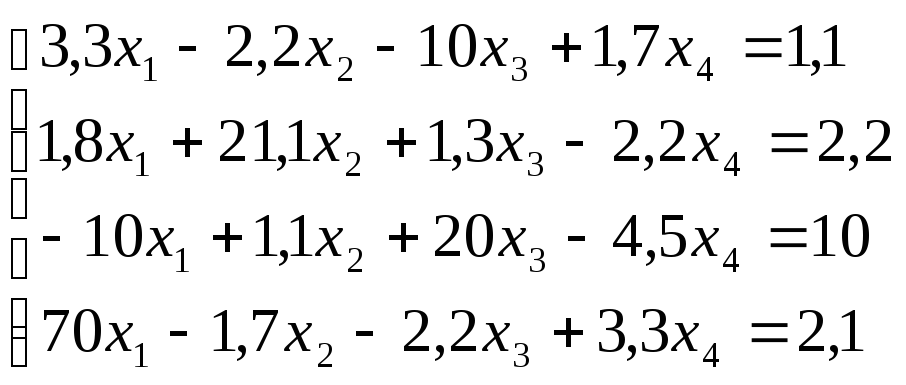
10.
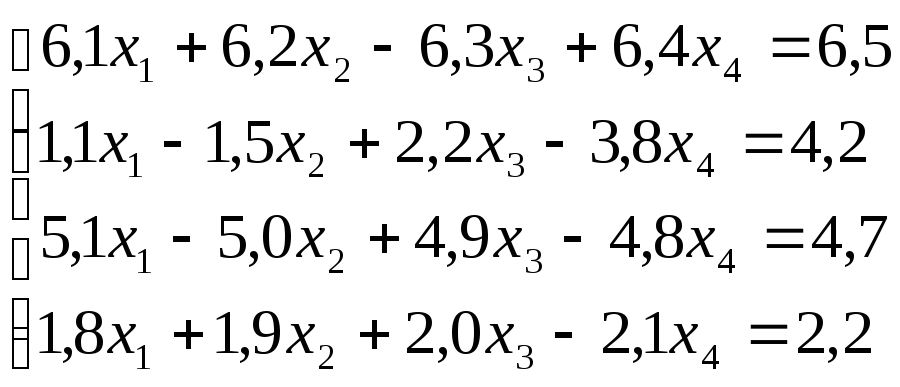 25.
25.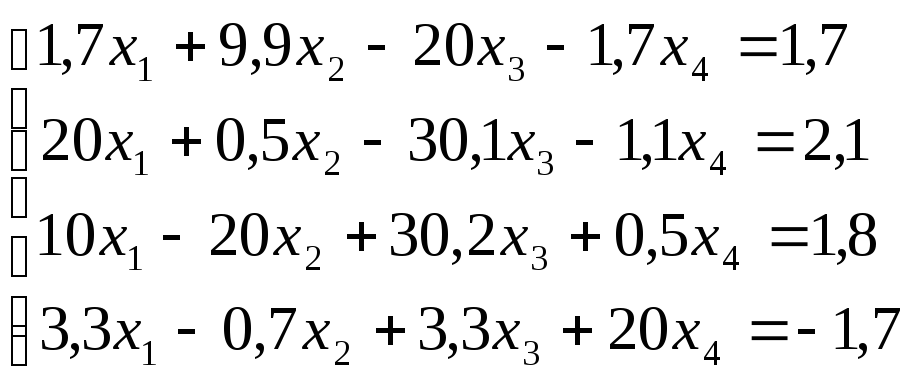
11.
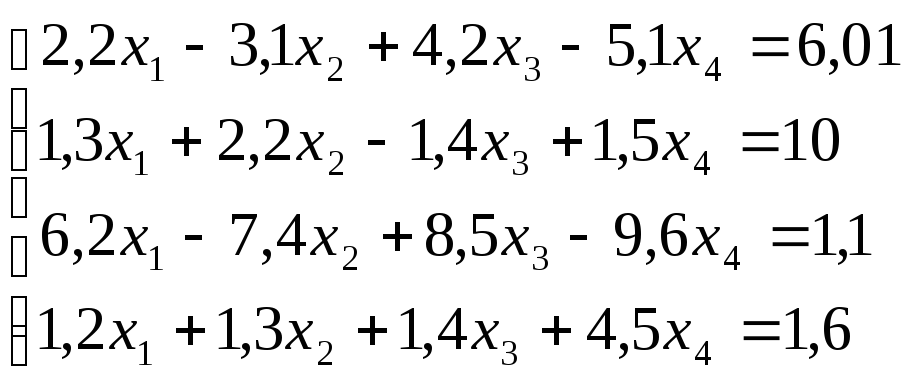 26.
26.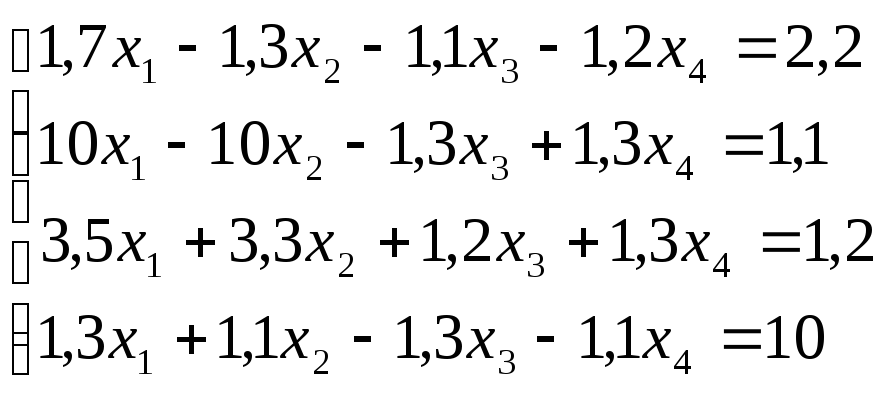
12.
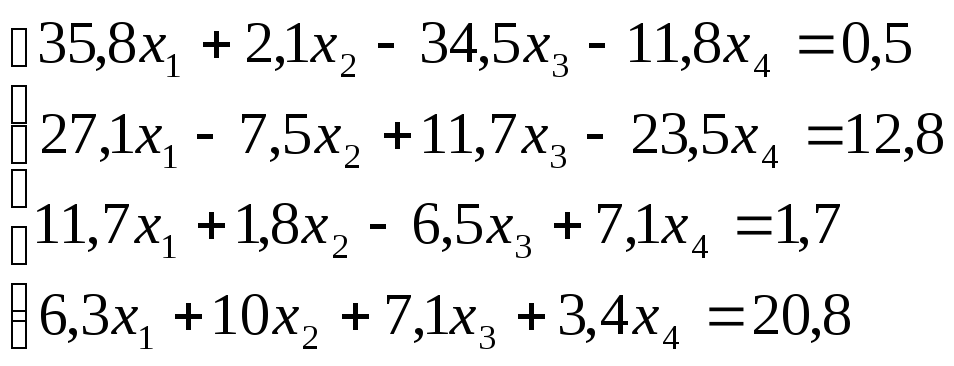 27.
27.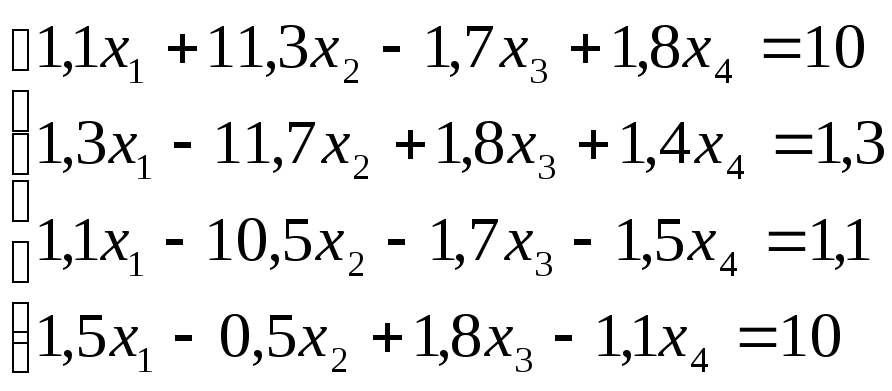
13.
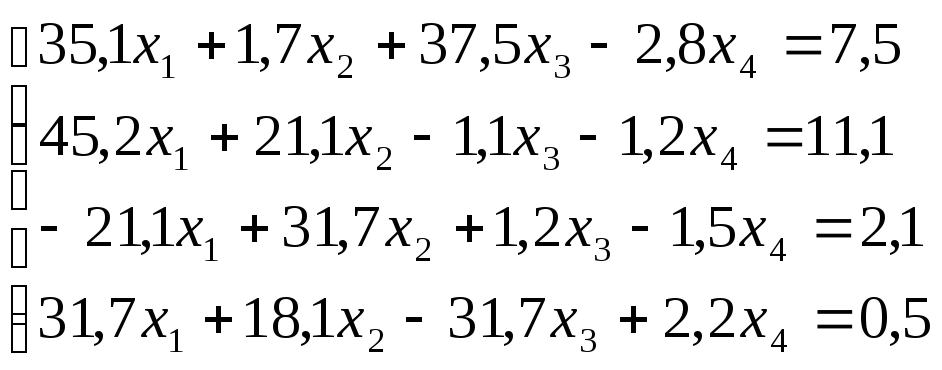 28.
28.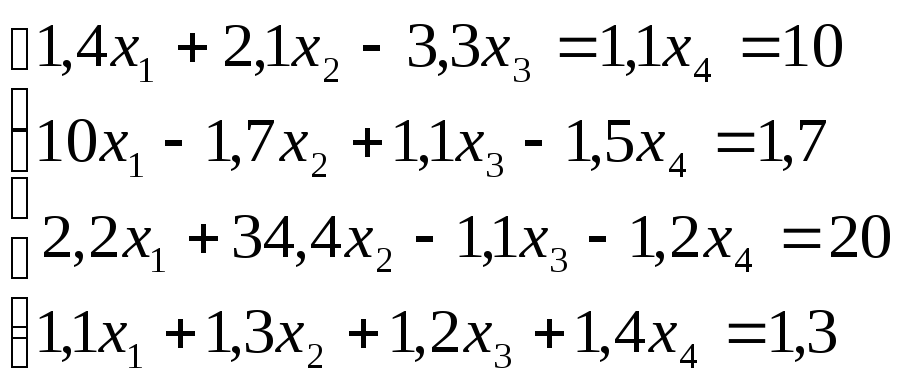
14.
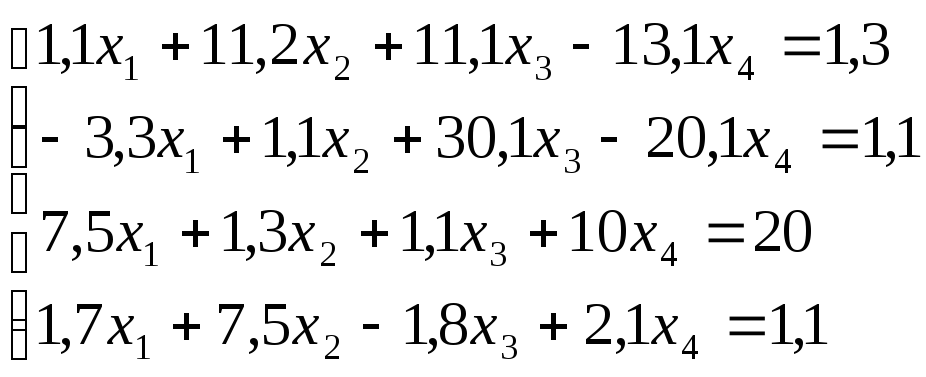 29.
29.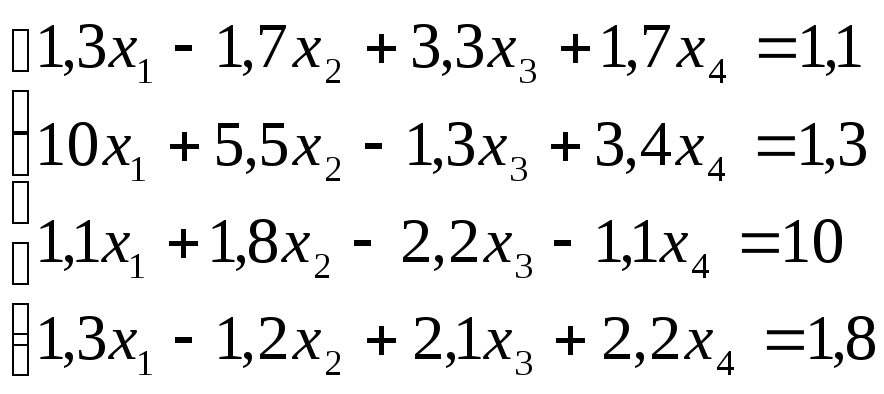
15.
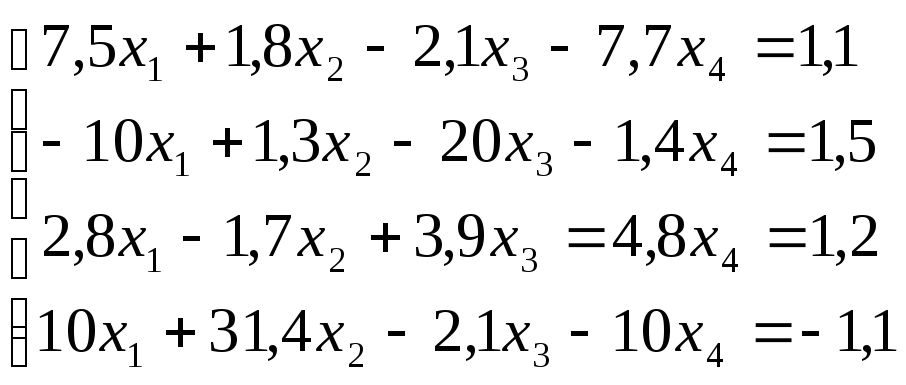 30.
30.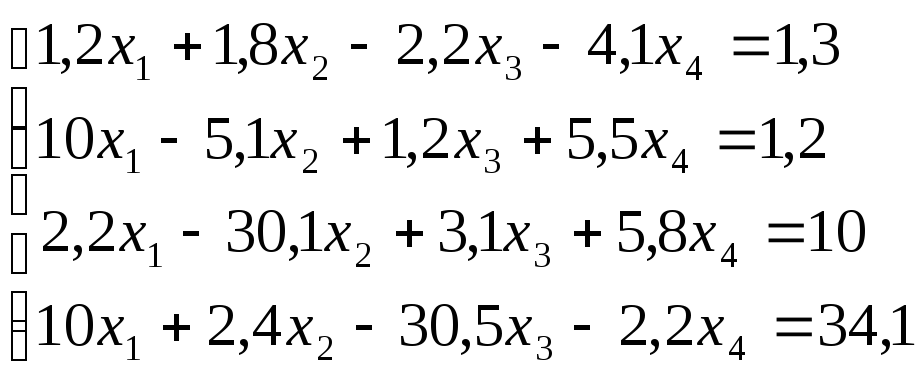
|
|
|
|
|
Свободные члены |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
После заполнения таблицы находим точные значения корней по формулам:
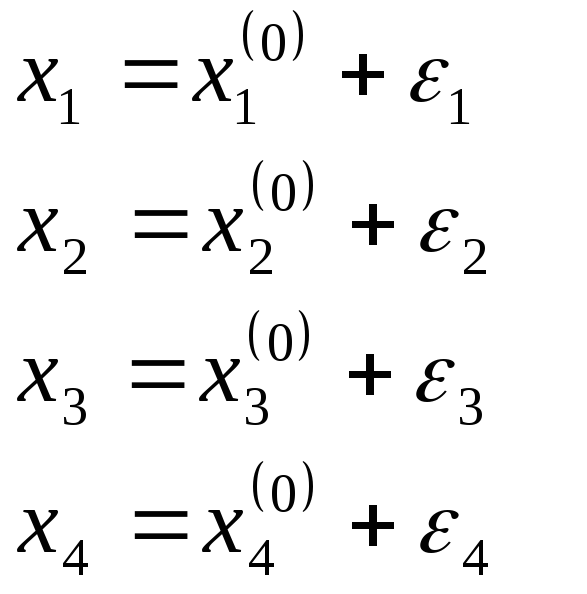
Лабораторная работа №9 «Метод Халецкого»
Решить
систему уравнений по схеме Халецкого
с точностью до ![]() .
.
1.
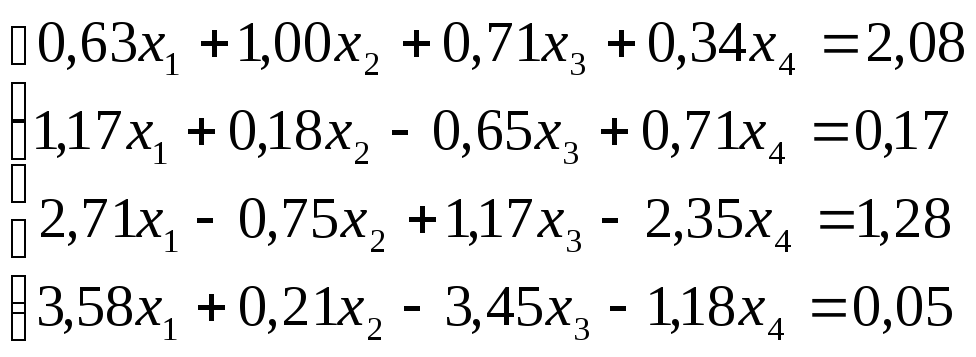 16.
16.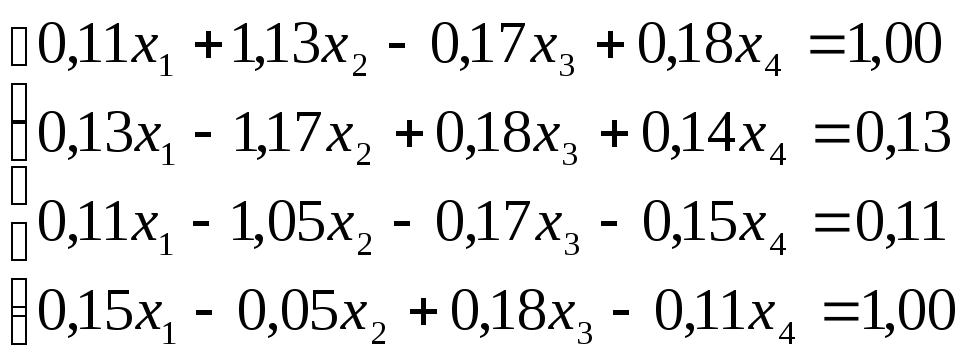
2.
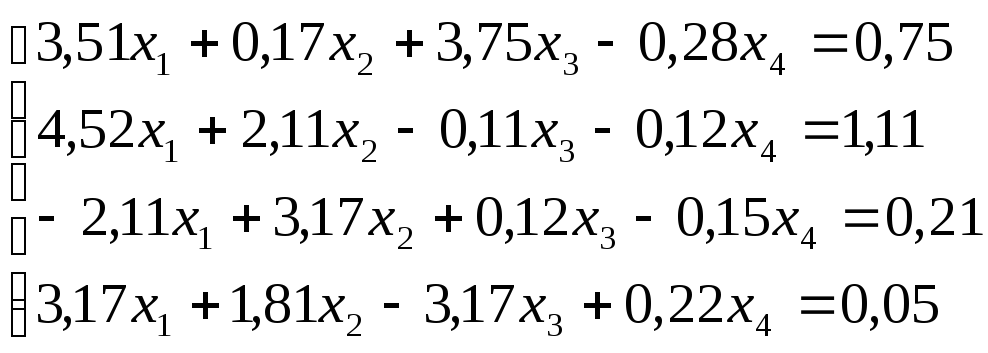 17.
17.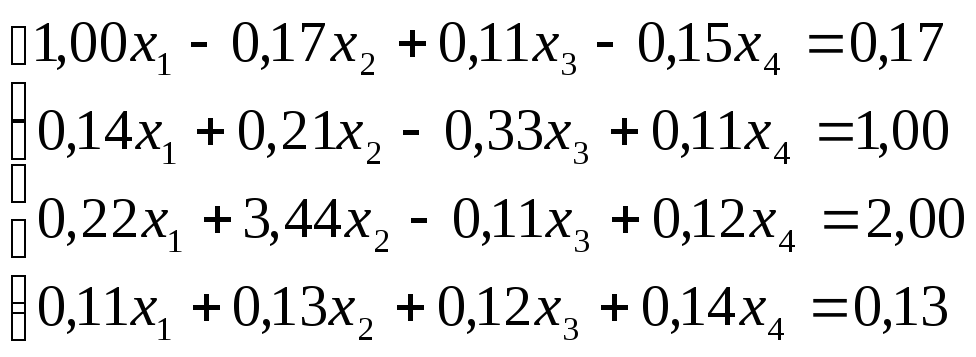
3.
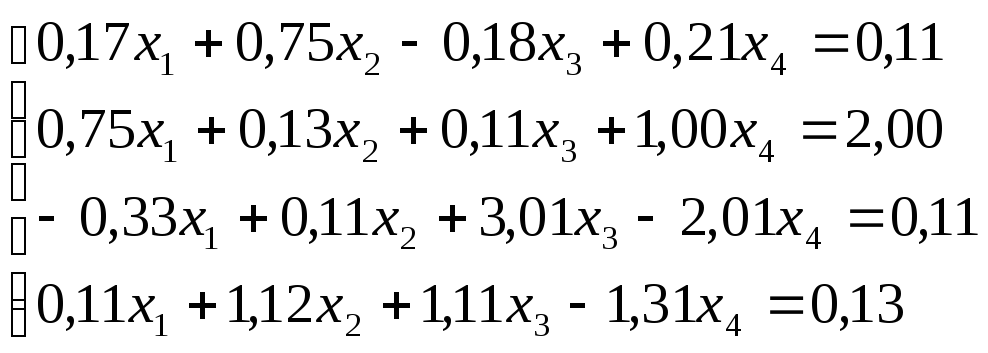 18.
18.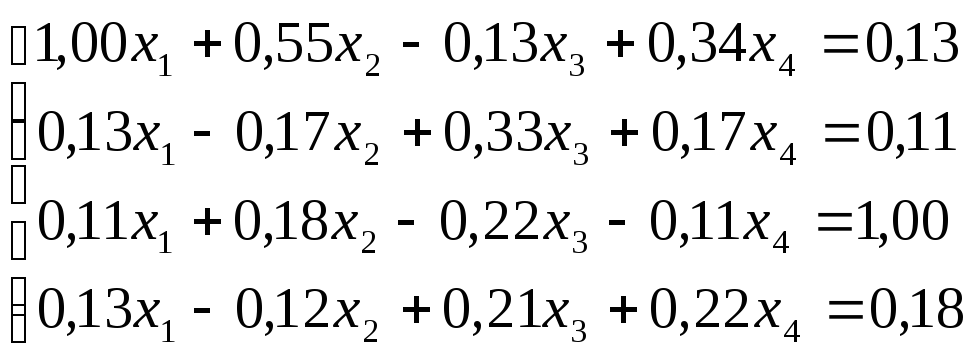
4.
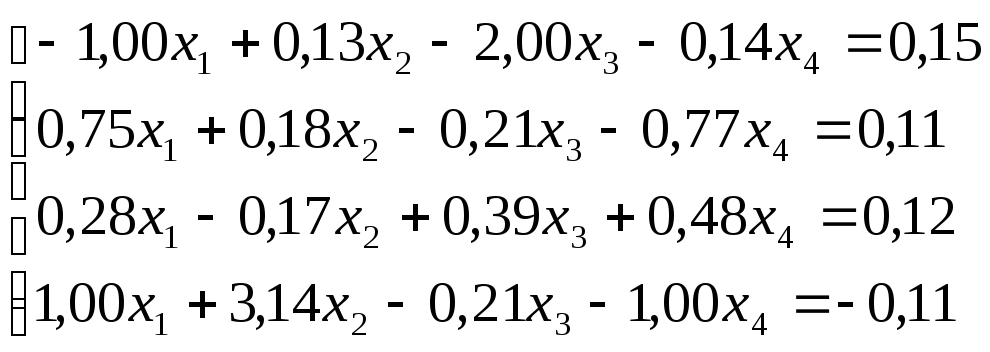 19.
19.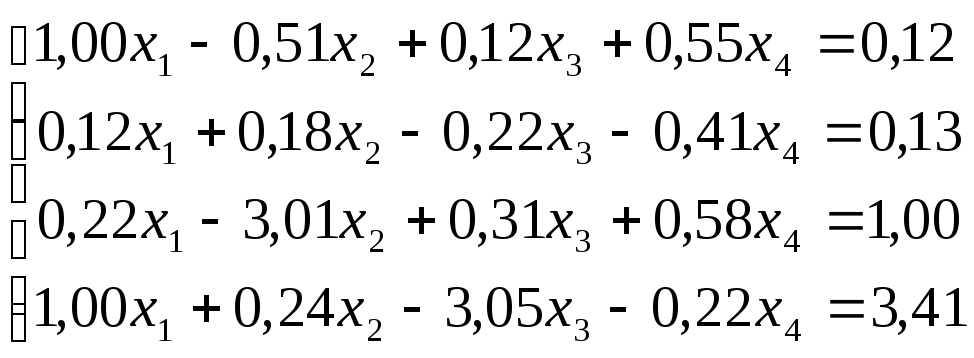
5.
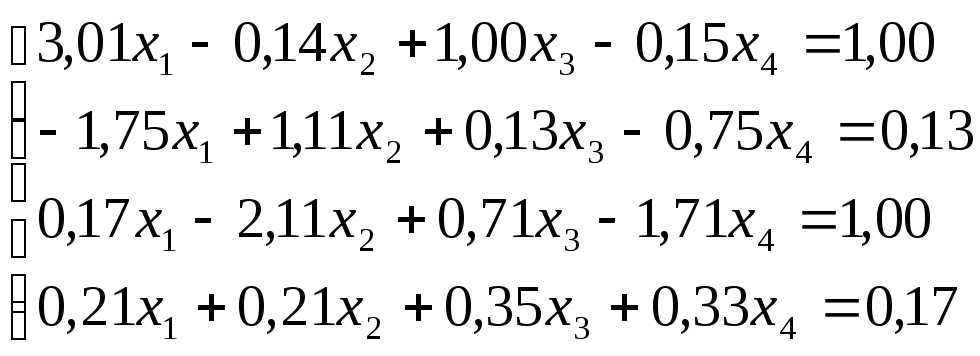 20.
20.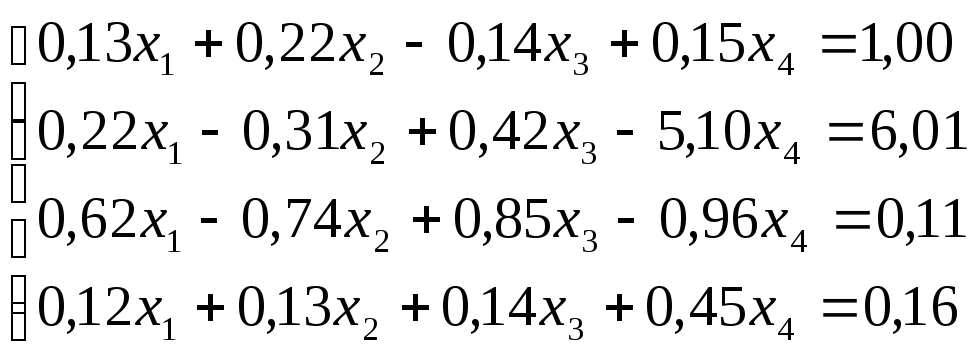
6.
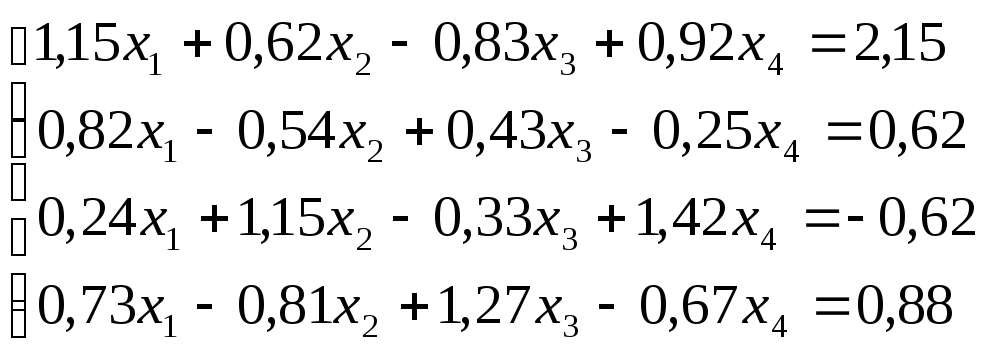 21.
21.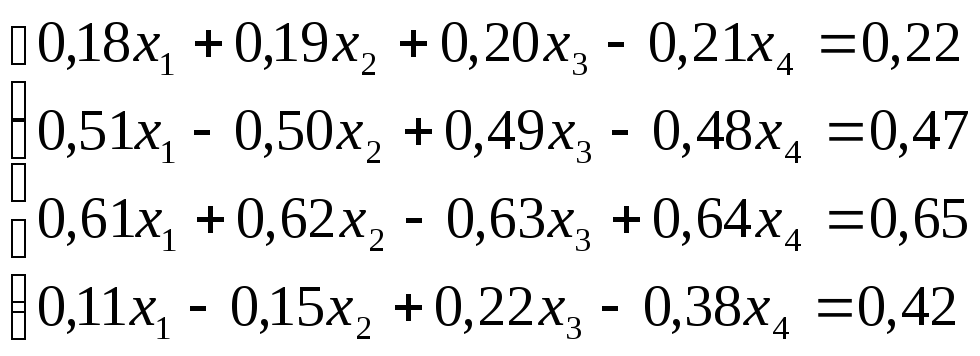
7.
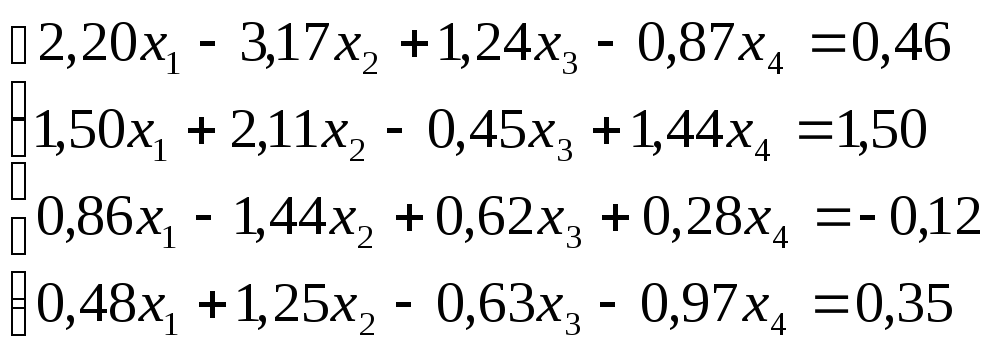 22.
22.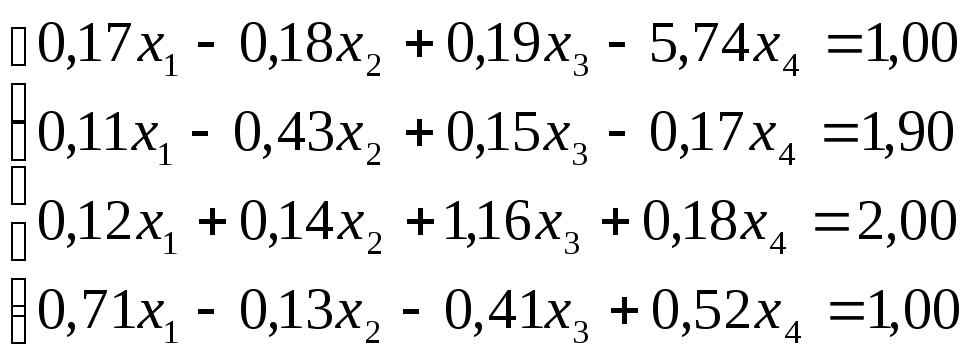
8.
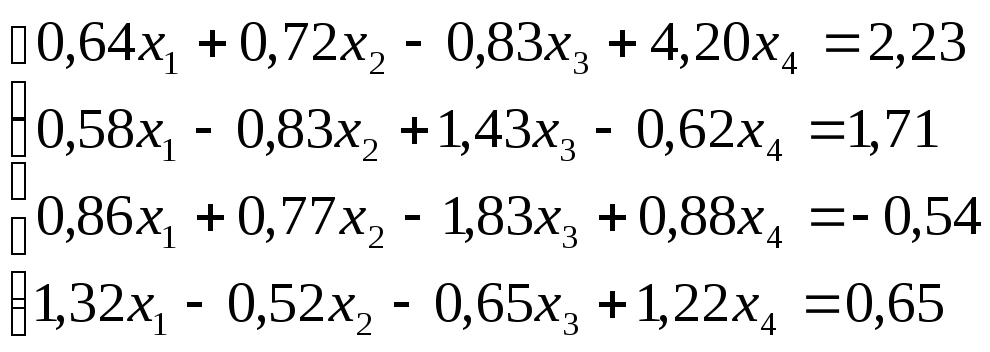 23.
23.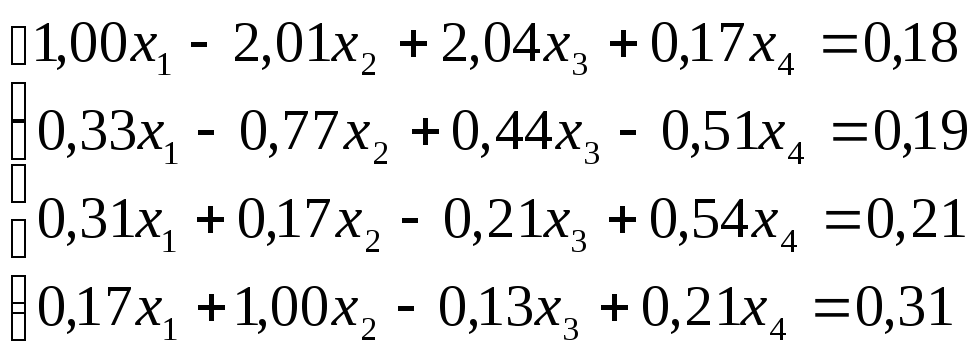
9.
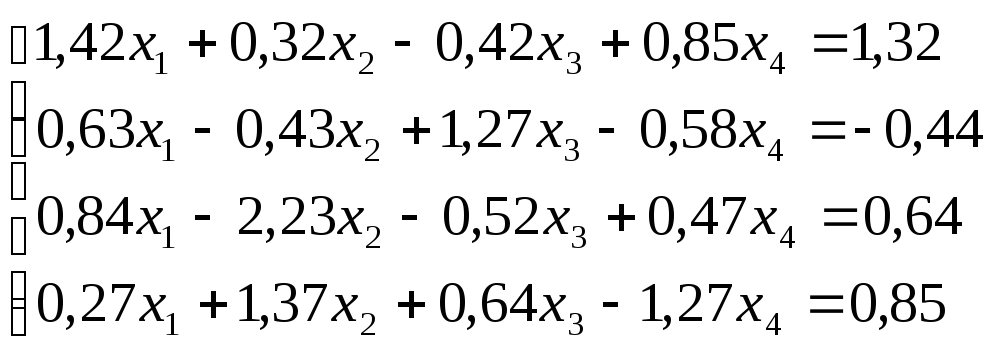 24.
24.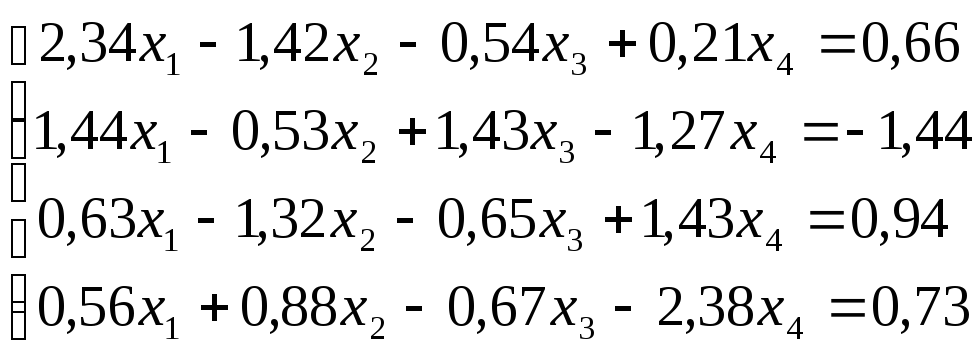
10.
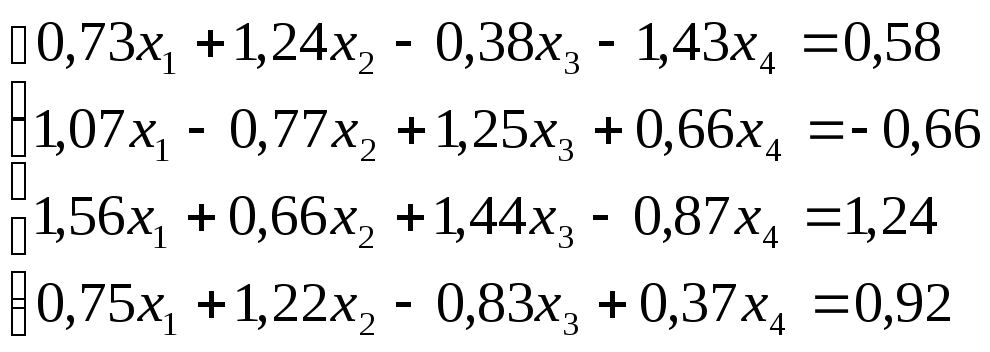 25.
25.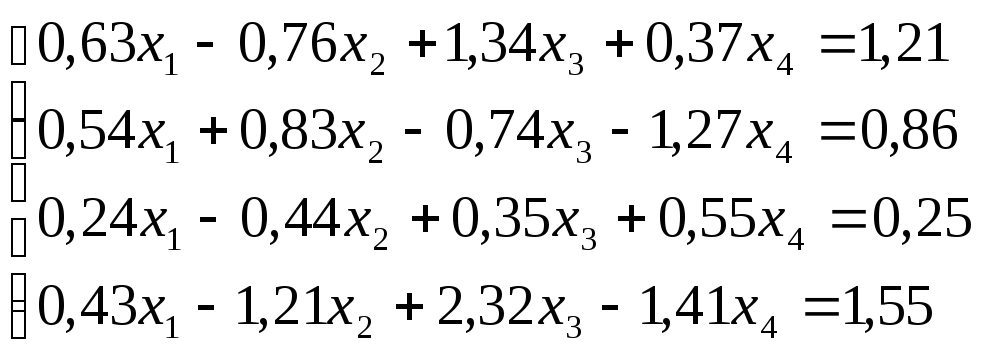
11.
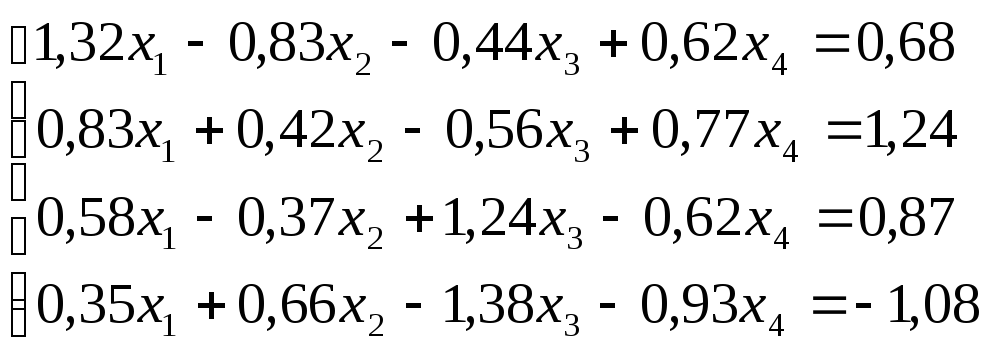 26.
26.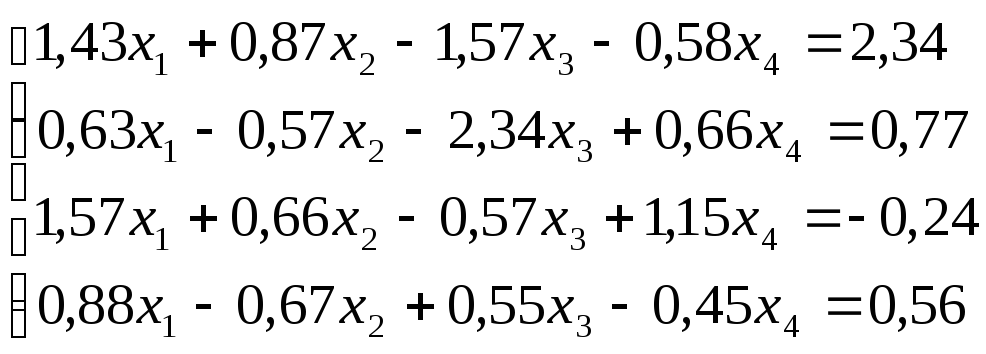
12.
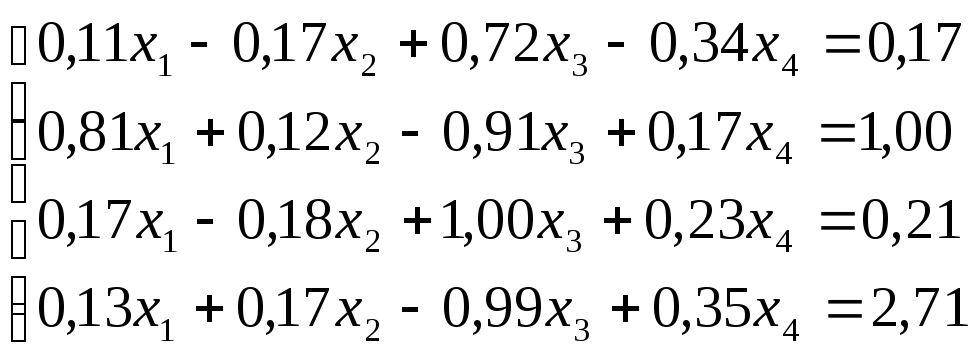 27.
27.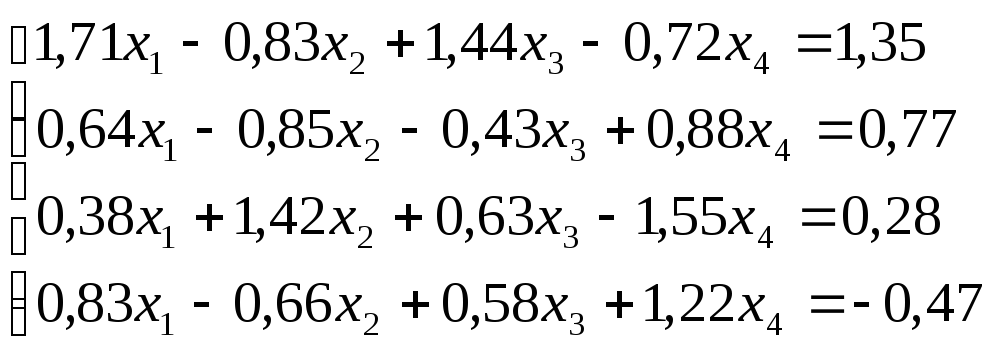
13.
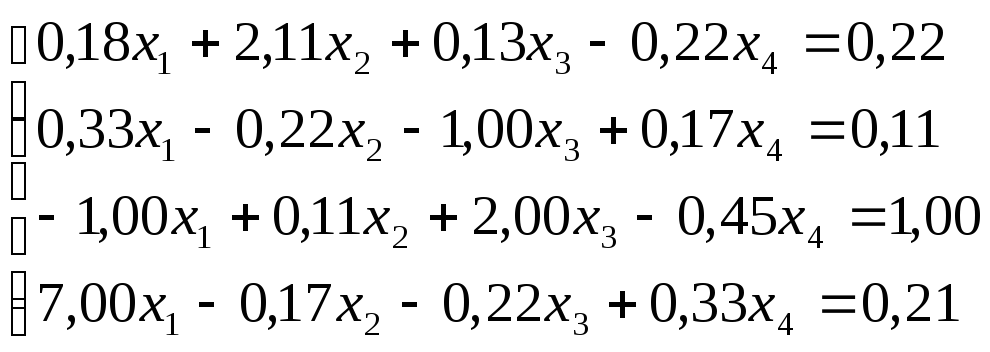 28.
28.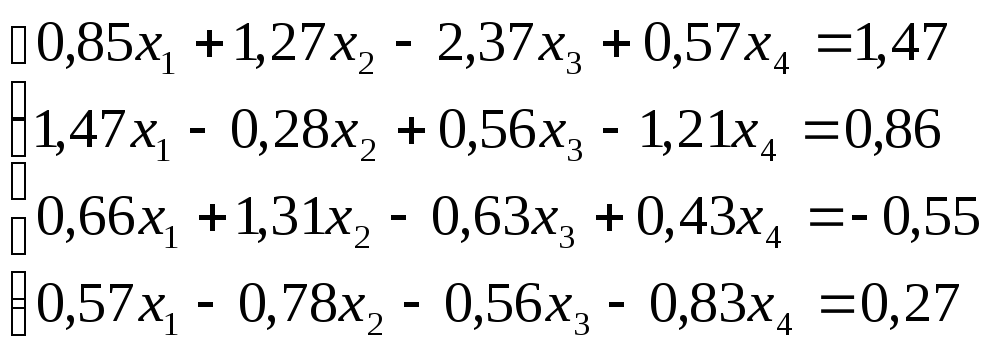
14.
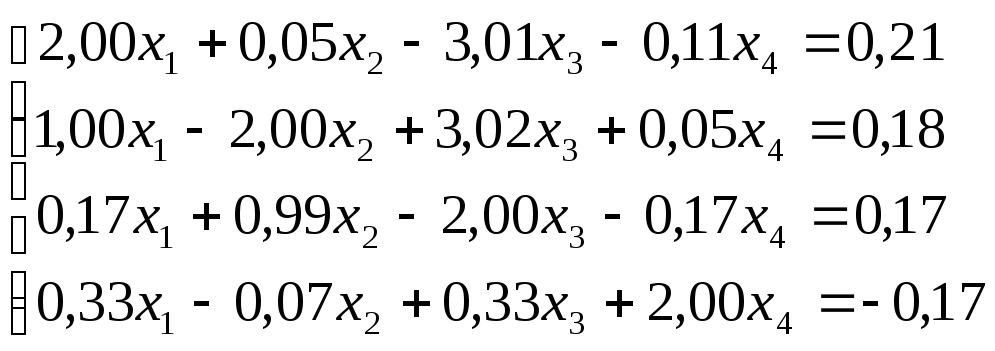 29.
29.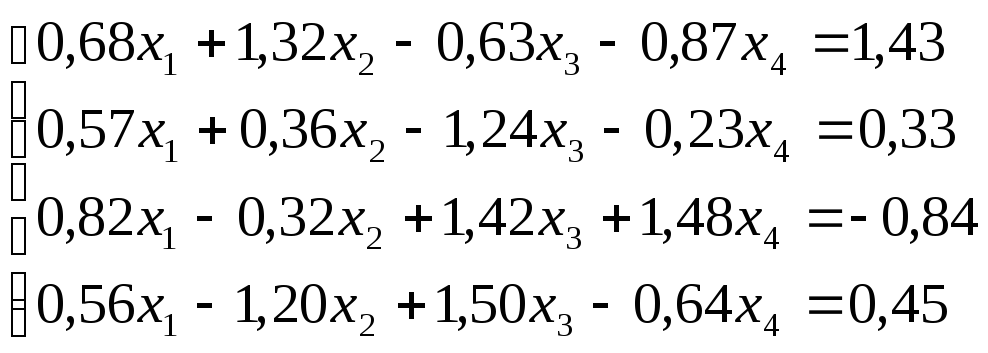
15.
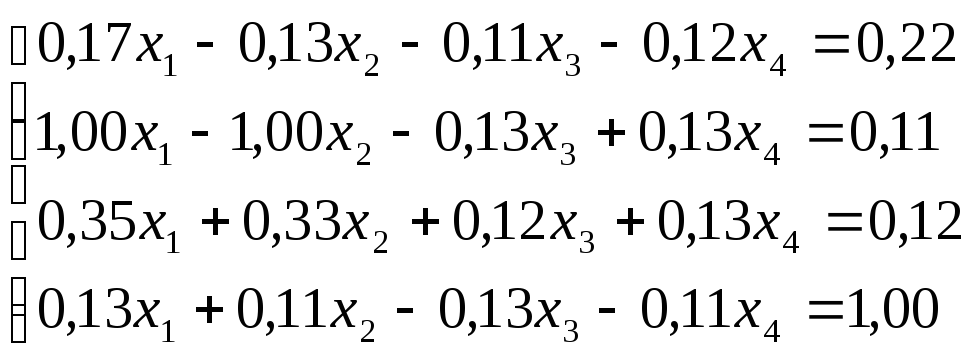 30.
30.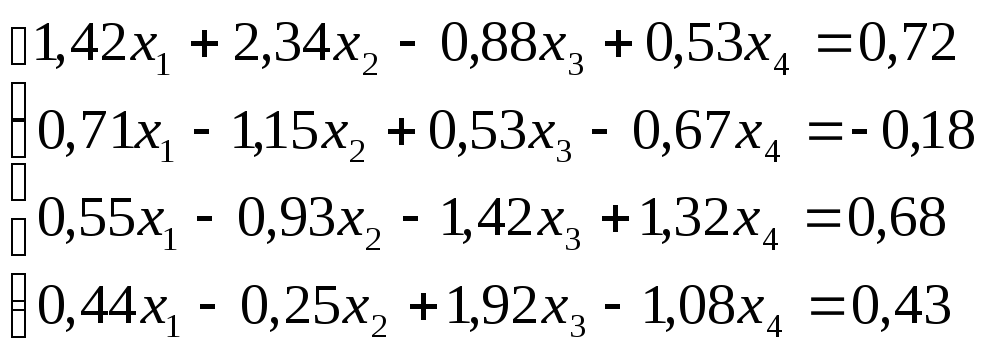
Схема Халецкого
|
|
|
|
|
|
Свободные члены |
|
I |
|
|
|
|
|
|
II |
|
|
|
|
|
|
III |
|
|
|
|
|
![]()
Схема Халецкого для решения системы уравнений (в общем виде)
|
Хi1 |
Хi2 |
Xi3 |
Xi4 |
Свободные члены |
Контрольные суммы |
|
a11 |
a12 |
a13 |
a14 |
a15 |
|
|
a21 |
a22 |
a23 |
a24 |
a25 |
|
|
a31 |
a32 |
a33 |
a34 |
a35 |
|
|
a41 |
a42 |
a43 |
a44 |
a45 |
|
|
b11 |
α12 |
α 13 |
α 14 |
α15 |
β1 |
|
b21 |
b22 |
α 23 |
α 24 |
α25 |
β2 |
|
b31 |
b32 |
b33 |
α 34 |
α35 |
β3 |
|
b41 |
b42 |
b43 |
b44 |
α45 |
β4 |
|
|
|
|
1 |
x4 |
|
|
|
|
1 |
|
x3 |
|
|
|
1 |
|
|
x2 |
|
|
1 |
|
|
|
x1 |
|
Вычислительные формулы:
![]() (i=1,2,3,4)
(i=1,2,3,4)
![]() (j=2,3,4,5),
(j=2,3,4,5),
![]() ,
,
![]()
![]() (i=2,3,4)
(i=2,3,4)
![]() (j=3,4,5),
(j=3,4,5),
![]() ,
,
![]()
![]() (i=3,4)
(i=3,4)
![]() (j=4,5),
(j=4,5),
![]() ,
,
![]()
![]() (i=4)
(i=4)
![]() (j=5),
(j=5),
![]() ,
,
![]()
Значения переменных вычисляются по схеме единственного деления:
![]() ,
,
![]() ,
проверка
,
проверка ![]() (i=4,3,2,1)
(i=4,3,2,1)
Порядок заполнения таблицы:
В первый раздел таблицы вписываем матрицу коэффициентов и свободные члены.
Элементы столбца
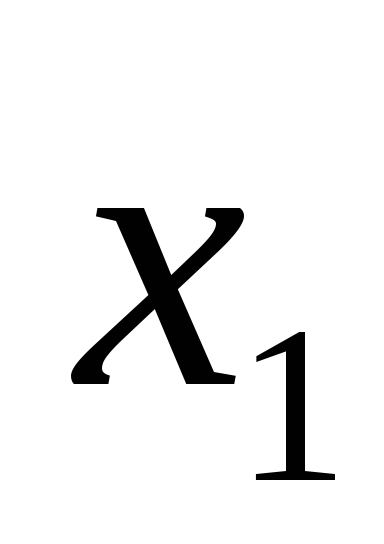 из раздела I переносим в
столбец
из раздела I переносим в
столбец 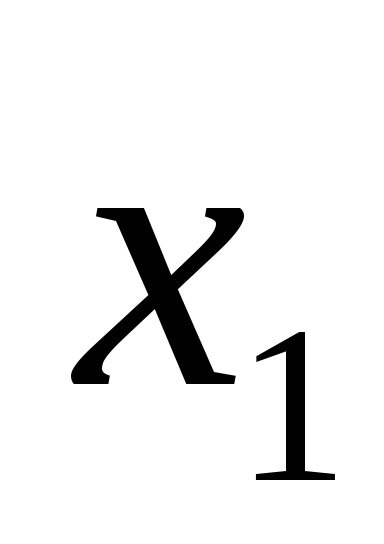 раздела II, т.к.
раздела II, т.к. 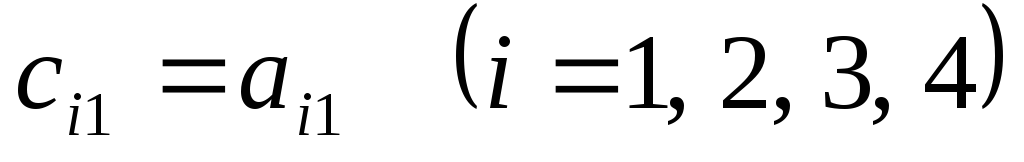 .
.Вычисляем элементы первой строки раздела II. Для этого делим все элементы первой строки раздела I на элемент
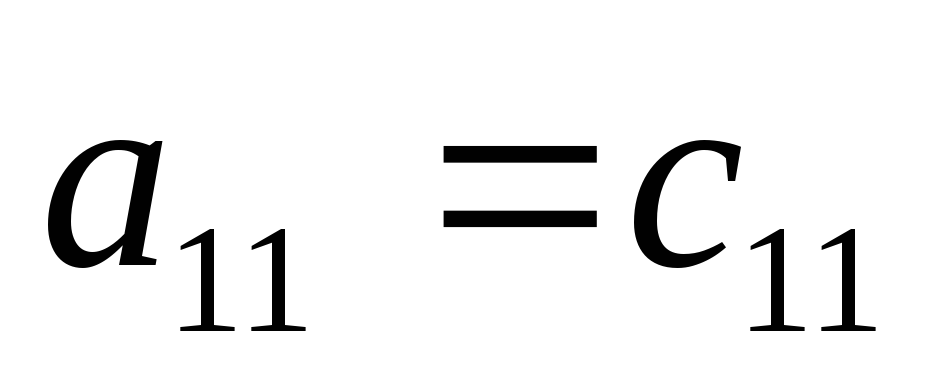 .
.
Заполняем столбец
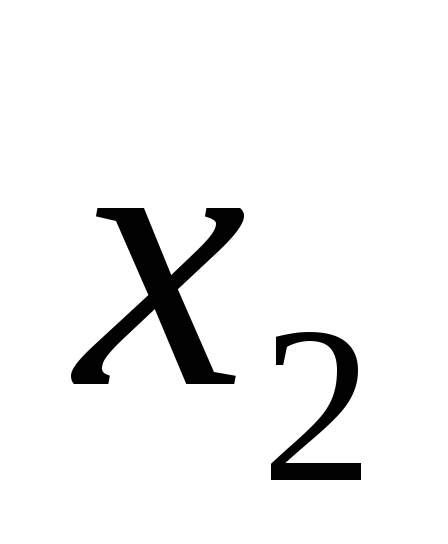 раздела II, начиная со
второй строки. Находим
раздела II, начиная со
второй строки. Находим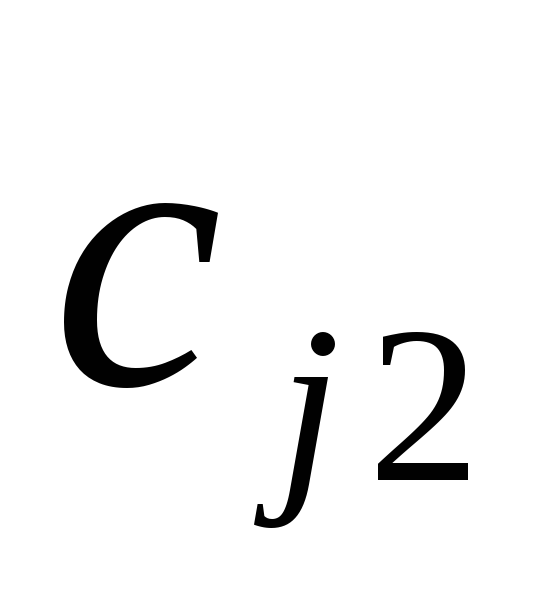 .
.Заполняем вторую строку раздела II, определяя
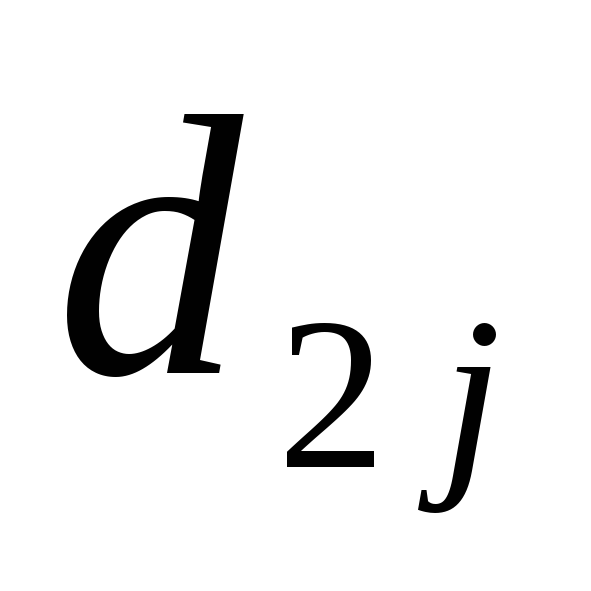 .
.Заполняем столбец
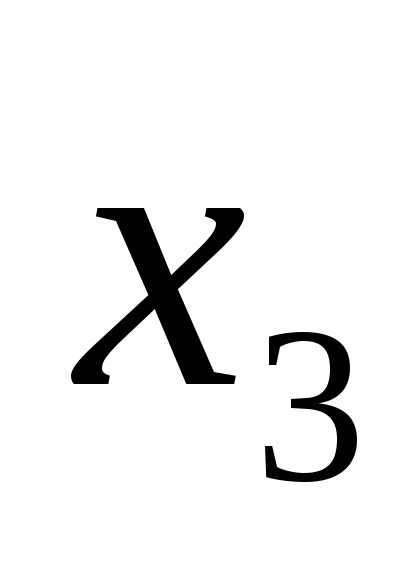 ,
вычисляя элементы
,
вычисляя элементы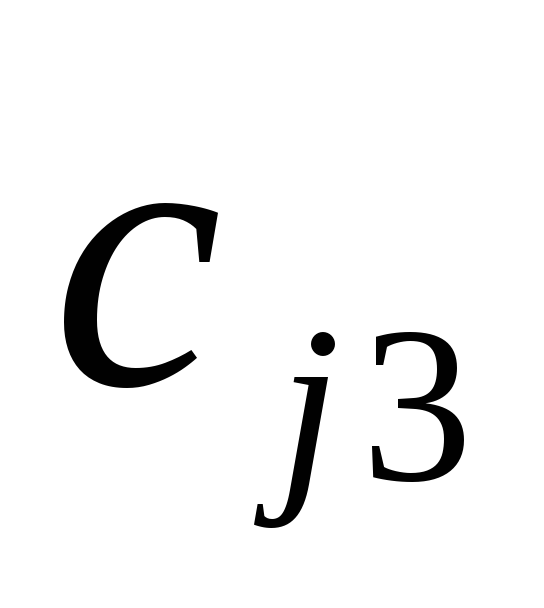 .
.Заполняем третью строку раздела II, определяя
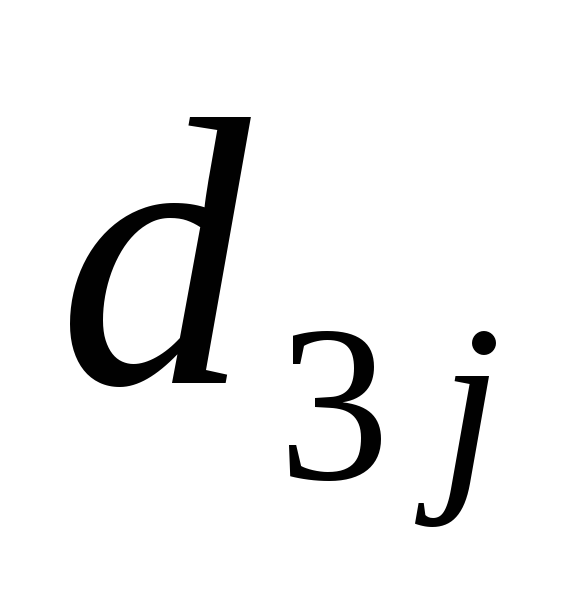 .
.Находим
 .
9.Определяем
.
9.Определяем .
10.Находим
.
10.Находим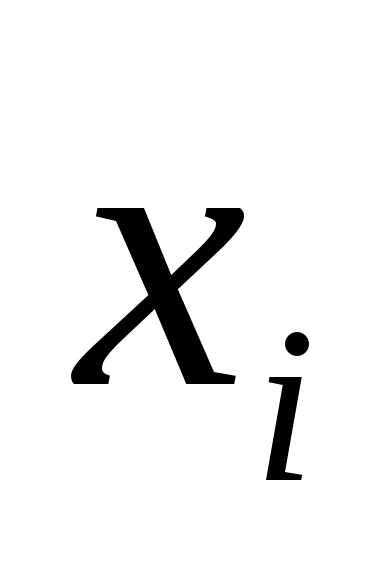 .
.