Образец выполнения задания:

1. На отрезке построить кубический сплайн шагом , удовлетворяющий на концах отрезка краевым условиям I типа и интерполирующий функцию . С помощью интерполяционной формулы вычислить приближенное значение .

Решение:

Будем искать кубическую параболу ,удовлетворяющую следующим условиям на концах отрезка и :

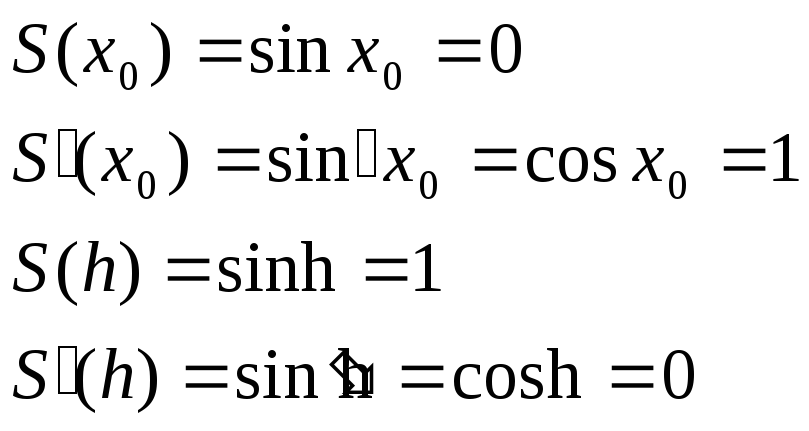
Воспользуемся формулой:

, .

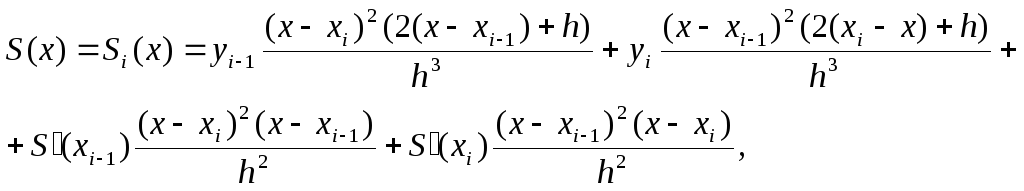
Получим:

()

Преобразуем:

.

Тогда .

2. Решить систему методом прогонки.

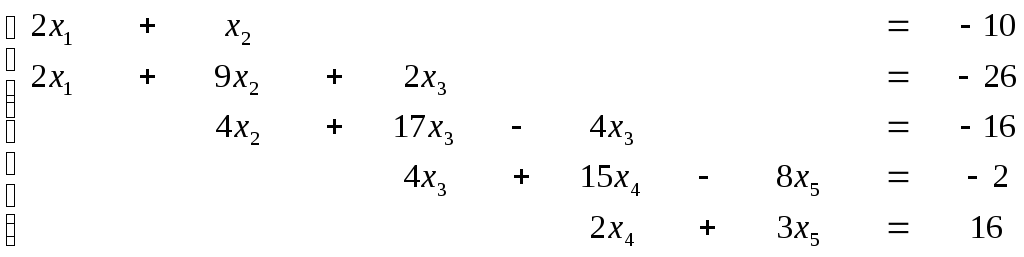
Решение:

; ;;

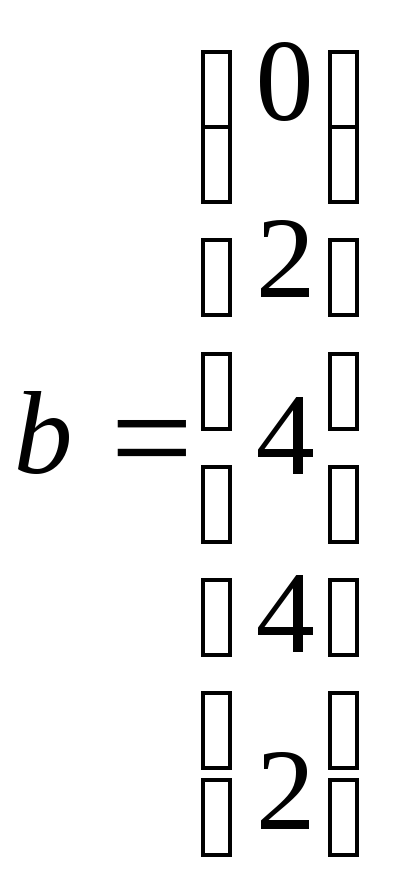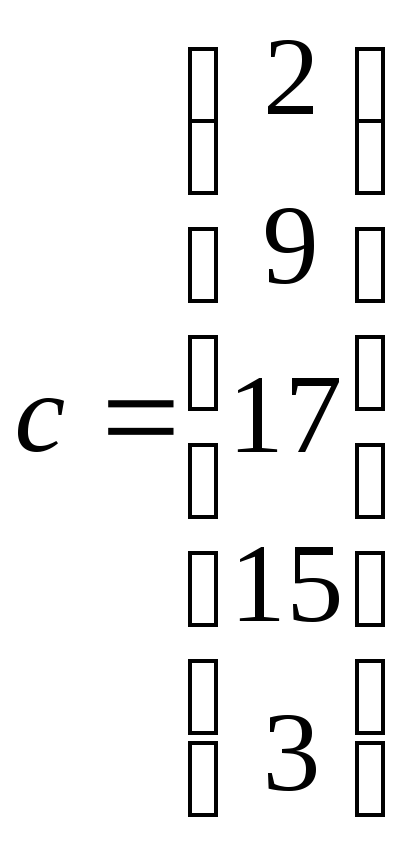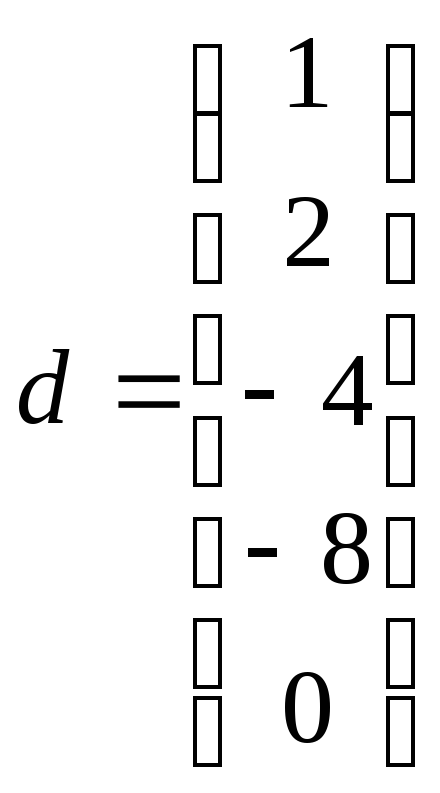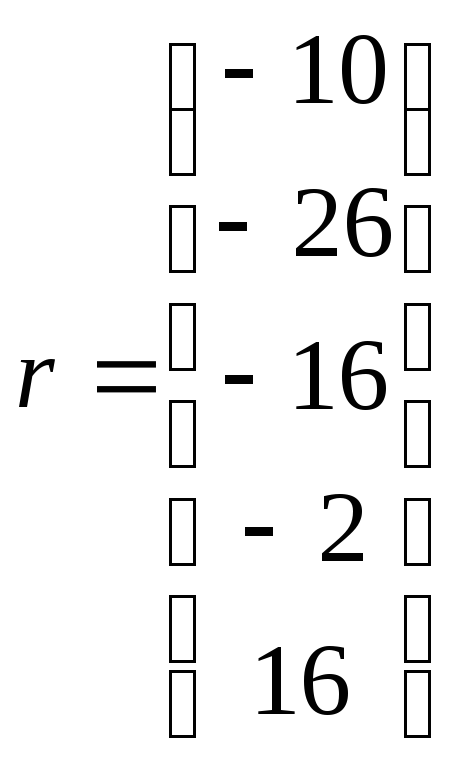
Воспользуемся формулами:

: ;

:;

()

i	bi	ci	di	ri	δi	λi	xi
1	0	2	1	-10	-0,5	-5	-4
2	2	9	2	-26	-0,25	-2	-2
3	4	17	-4	-16	0,25	-0,5	0
4	4	15	-8	-2	0,5	0	2
5	2	3	0	16	0	4	4

Ответ: .

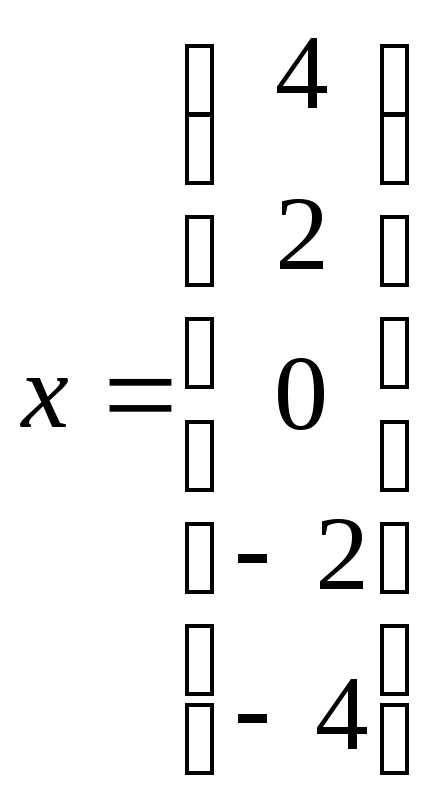Лабораторная работа17 Среднеквадратическое приближение

Задание: Установить вид эмпирической формулы , используя аппроксимирующую зависимость с тремя параметрами a, b и c, имеющую вид . Опытные данные определены таблицей.

Вариант №1

xi	1	2	4	5
yi	3	0	2	1

Вариант №2

xi	0	1	4	5
yi	2	1	5	3

Вариант №3

xi	2	3	4	5
yi	1	2	3	4

Вариант №4

xi	0	1	5	6
yi	3	6	2	1

Вариант №5

xi	4	5	6	7
yi	3	0	1	2

Вариант №6

xi	1	2	4	5
yi	5	2	6	0

Вариант №7

xi	2	3	4	5
yi	7	2	5	3

Образец выполнения задания:

xi	0	1	3	4
yi	4	0	1	2

Для нахождения a, b и c составим систему уравнений вида:

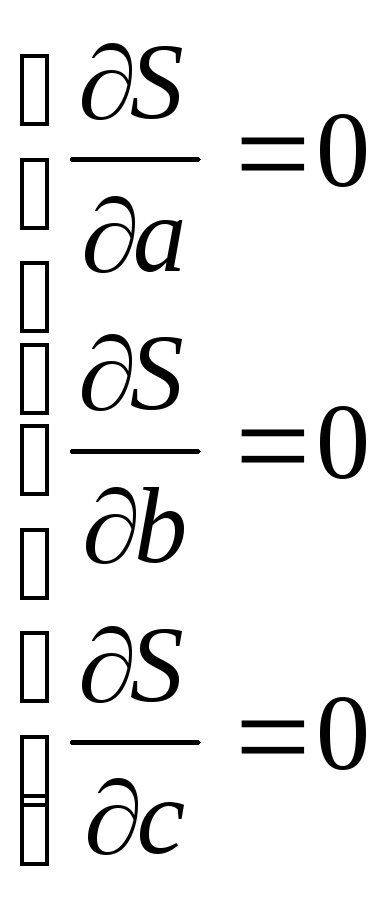
Отсюда получаем систему трех линейных уравнений с тремя неизвестными:

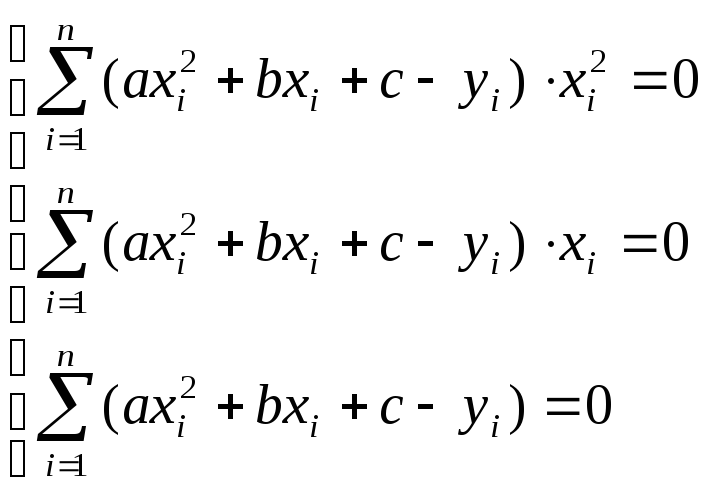
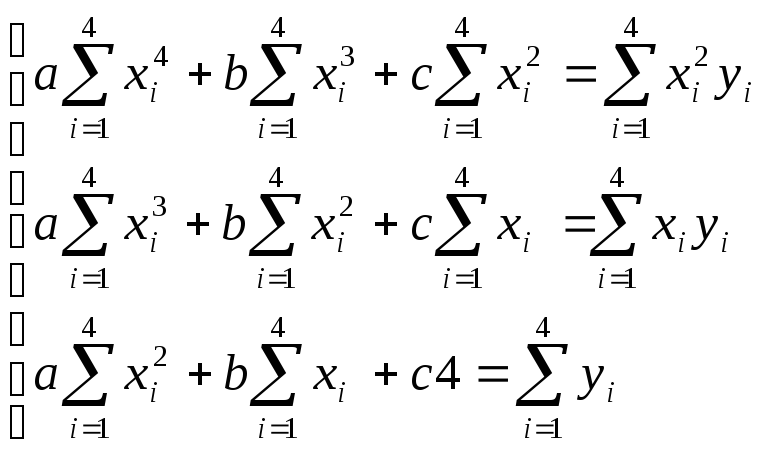
xi	yi	xi2	xi3	xi4	xiyi	xi2yi
0	4	0	0	0	0	0
1	0	1	1	1	0	0
3	1	9	27	81	3	9
4	2	16	64	256	8	32
Сумма	7	26	92	338	11	41

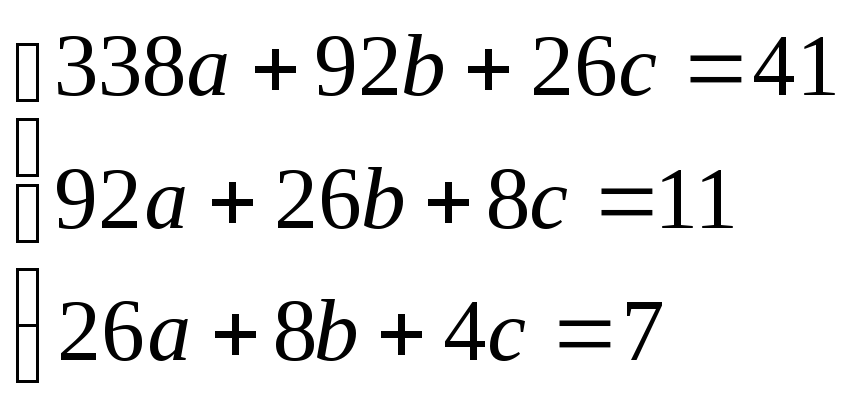
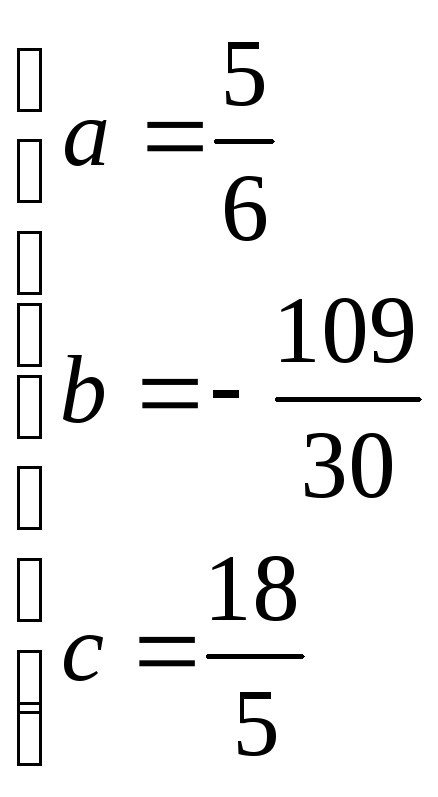
Эмпирическая формула представляет собой функцию:

.

Лабораторная работа18 Ортогональные многочлены Чебышева

Задание:

1. На множестве точек 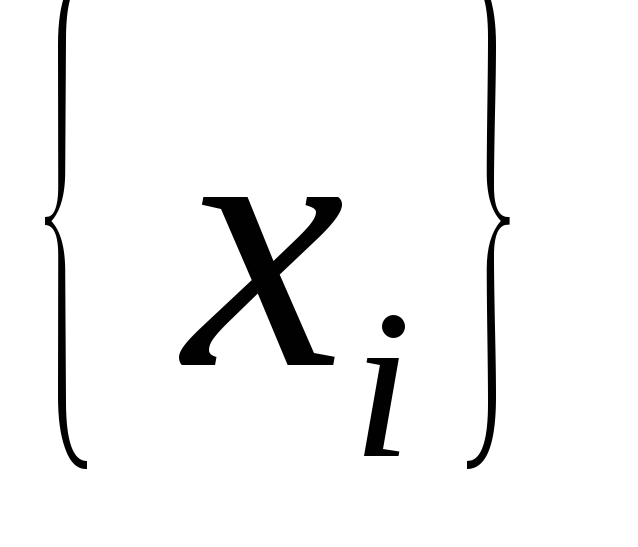определить ортогональные многочлены Чебышева и вычислить их нормы.

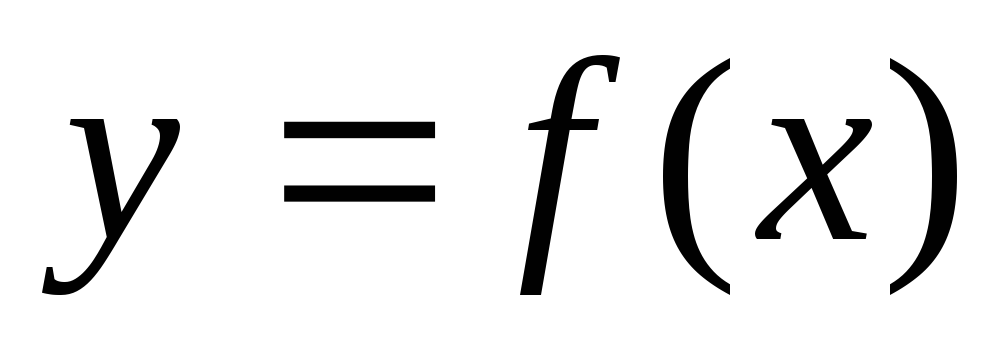2. Требуется аппроксимировать функцию алгебраическими многочленами наилучшего среднеквадратического приближения , , , .

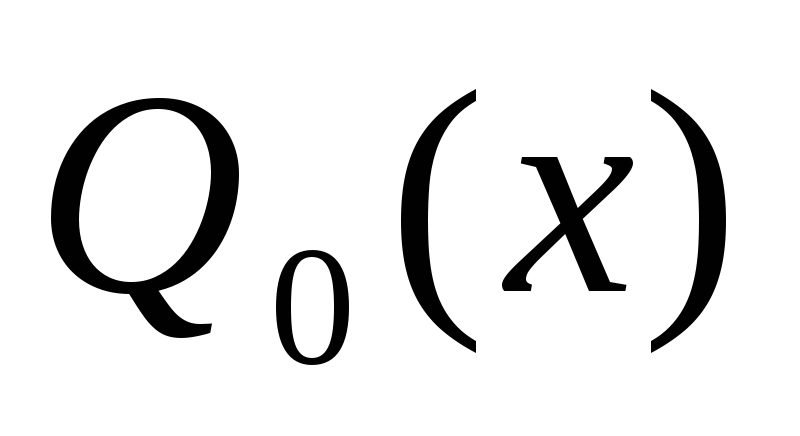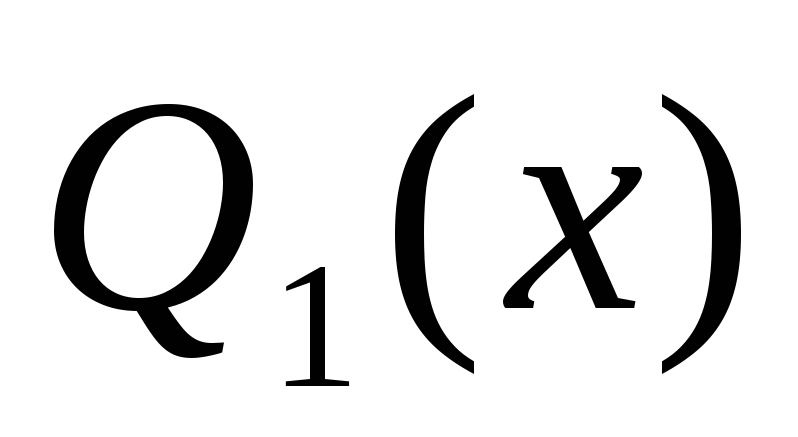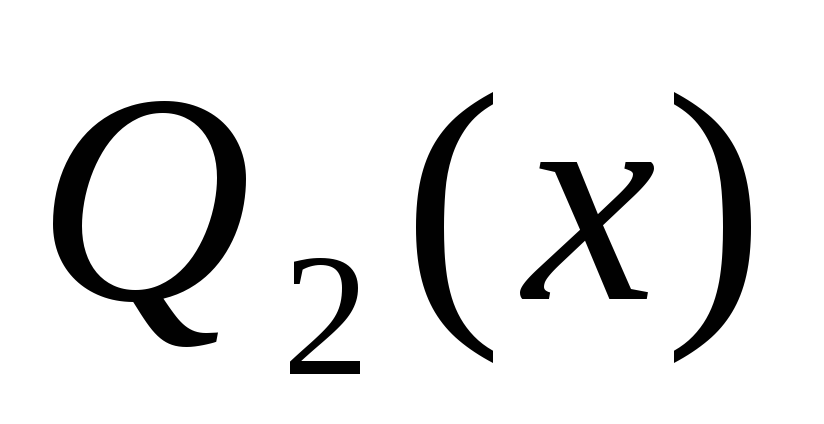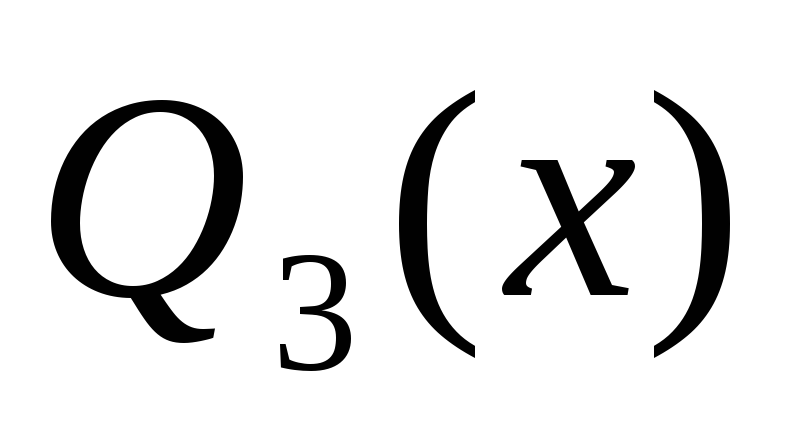Вариант №1

1.

2

xi	1	2	3	4	5
yi	1,1	1,4	1,6	1,7	1,9

.

Вариант №2

1.

2

xi	1	2	3	4	5
yi	1,05	1,55	1,7	1,75	1,8

.

Вариант №3

1.

2

xi	2	3	4	5	6
yi	0,4	0,55	0,13	0,09	0,07

.

Вариант №4

1.

2

xi	1	2	3	4	5
yi	2	2,69	3,1	3,39	3,61

.

Вариант №5

1.

2

xi	1	2	3	4	5
yi	1,1	1,55	1,9	2,3	2,6

.

Вариант №6

1.

2

xi	1	2	3	4	5
yi	7,1	6,1	4,9	4	3,1

.