
- •Лабораторная работа №1 «Элементарная теория погрешностей»
- •Лабораторная работа №2 «Элементарная теория погрешностей»
- •Лабораторная работа №3 «Метод половинного деления»
- •Лабораторная работа №4: «Решение нелинейных уравнений методом хорд и касательных».
- •2)Метод касательных (Ньютона).
- •Лабораторная работа №5 «Комбинированный метод»
- •Лабораторная работа №6: «Решение нелинейных уравнений методом простой итерации».
- •Метод главных элементов для решения системы уравнений
- •Лабораторная работа №8 «Метод Гаусса»
- •Лабораторная работа №9 «Метод Халецкого»
- •Порядок заполнения таблицы:
- •Лабораторная работа №10 «Метод квадратных корней»
- •Лабораторная работа №11 «Метод итераций»
- •Лабораторная работа № 12 «Метод Зейделя»
- •Лабораторная работа13. Интерполирование функции многочленом Лагранжа.
- •Лабораторная работа14. Интерполирование функции многочленом Ньютона.
- •Лабораторная работа15. Сплайновая интерполяция.
- •Лабораторная работа16 Интерполяция функции кубическим сплайном. Метод прогонки.
- •Образец выполнения задания:
- •Лабораторная работа17 Среднеквадратическое приближение
- •Образец выполнения задания:
- •Лабораторная работа18 Ортогональные многочлены Чебышева
- •Образец выполнения задания:
- •Лабораторная работа19. Вычисление определенных интегралов по формуле трапеций и формуле Симпсона, по формуле левых, правых и средних прямоугольников.
- •3) Вычислить определенный интеграл по формуле левых и правых прямоугольников.
- •4) Вычислить определенный интеграл по формуле средних прямоугольников.
- •Лабораторная работа 20. Метод Эйлера с уточнением
- •Л/р 21«Численное решение ду первого порядка методом Рунге-Кутты 4-го порядка».
- •Л/р22 «Решение ду первого порядка методом Адамса-Башфорта».
- •Лабораторная работа 24
- •4. Минимизация функции f(X) методом барьерных функций:
Лабораторная работа №1 «Элементарная теория погрешностей»
Задание 1. Выполнить последовательные округления следующих чисел:
1.
а) ![]() ;
б)
;
б) ![]() ;
16. а)
;
16. а) ![]() б)
б) ![]() ;
;
2.
а) ![]() б)
б) ![]() ;
17. а)
;
17. а) ![]() б)
б) ![]()
3.
а) ![]() б)
б) ![]() 18. а)
18. а) ![]() б)
б) ![]()
4.
а) ![]() б)
б) ![]() 19. а)
19. а) ![]() б)
б) ![]()
5.
а) ![]() б)
б) ![]() ;
20. а)
;
20. а) ![]() б)
б) ![]()
6.
а) ![]() б)
б) ![]() ;
21. а)
;
21. а) ![]() б)
б) ![]()
7.
а) ![]() б)
б) ![]() 22. а)
22. а) ![]() б)
б) ![]()
8.
а) ![]() б)
б) ![]() 23. а)
23. а) ![]() б)
б) ![]()
9.
а) ![]() б)
б) ![]() ;
24. а)
;
24. а) ![]() б)
б) ![]()
10.
а) ![]() б)
б) ![]() 25. а)
25. а) ![]() б)
б) ![]()
11.
а) ![]() б)
б) ![]() 26. а)
26. а) ![]() б)
б) ![]()
12.
а) ![]() б)
б) ![]() 27. а)
27. а) ![]() б)
б) ![]()
13.
а) ![]() б)
б) ![]() 28. а)
28. а) ![]() б)
б) ![]()
14.
а) ![]() б)
б) ![]() 29. а)
29. а) ![]() б)
б) ![]()
15.
а) ![]() б)
б) ![]() 30. а)
30. а) ![]() б)
б) ![]() .
.
Задание 2. Определить, какое из равенств точнее.
1.
![]() ;
16.
;
16.![]() ;
;
2.
![]() ;
17.
;
17.![]() ;
;
3.
![]() ;
18.
;
18.![]() ;
;
4.
![]() ;
19.
;
19.![]() ;
;
5.
![]() ;
20.
;
20.![]() ;
;
6.
![]() ;
21.
;
21.![]() ;
;
7.
![]() ;
22.
;
22.![]() ;
;
8.
![]() ;
23.
;
23.![]() ;
;
9.
![]() ;
24.
;
24.![]() ;
;
10.
![]() ;
25.
;
25.![]() ;
;
11.
![]() ;
26.
;
26.![]() ;
;
12.
![]() ;
27.
;
27.![]() ;
;
13.
![]() ;
28.
;
28.![]() ;
;
14.
![]() ;
29.
;
29. ![]() ;
;
15.
![]() ;
30.
;
30. ![]() .
.
Пример 1. Выполнить последовательные округления следующих чисел:
а)
![]() ;
б)
;
б)![]() .
.
Решение.
а)
 б)
б) 
Пример
2. Определить, какое
из равенств точнее: ![]() или
или ![]() .
.
Решение.
Берем числа с большим числом десятичных знаков:
![]() .
.
Определяем предельные абсолютные погрешности, округляя их с избытком:
![]() ;
;
![]() .
.
Находим предельные относительные погрешности:
![]() ;
;
![]() .
.
Т.к.
![]() ,
то первое равенство точнее.
,
то первое равенство точнее.
Лабораторная работа №2 «Элементарная теория погрешностей»
Вычислить и определить погрешности результата.
Вычислить и определить погрешности результата.
Вычислить, пользуясь правилами подсчета цифр.
а)
 ;
б)
;
б)
 ;
в)
;
в) .
.а)
 ;
б)
;
б)
 в)
в)
а)
 б)
б)
 в)
в)
а)
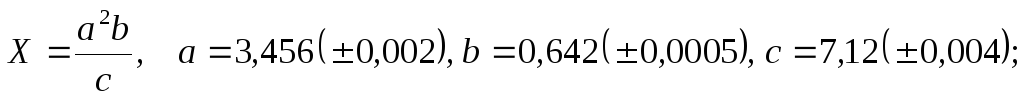 б)
б)
 в)
в)
а)
 б)
б)
 в)
в)
а)
 б)
б)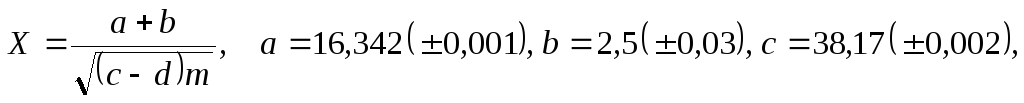
 в)
в)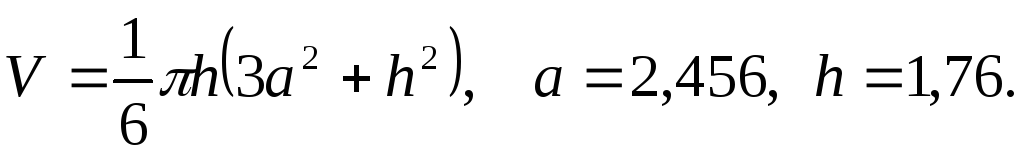
а)
 б)
б)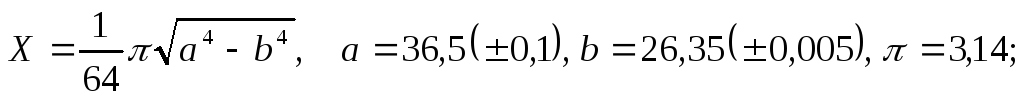 в)
в)
а)
 б)
б)
 в)
в)
а)
 б)
б)
 в)
в) ,
где
,
где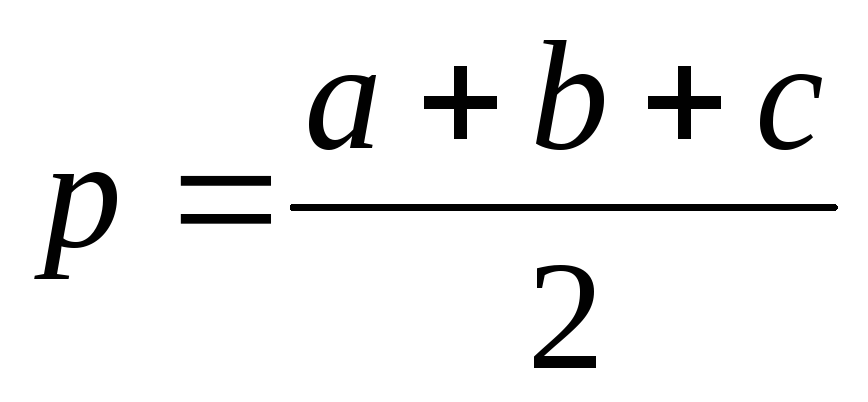 ,
,
а)
 б)
б) в)
в)
а)
 ;
б)
;
б)
 ;
в)
;
в) .
.а)
 ;
б)
;
б)
 в)
в)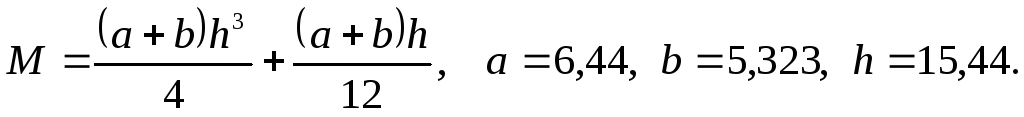
а)
 б)
б)
 в)
в)
а)
 б)
б)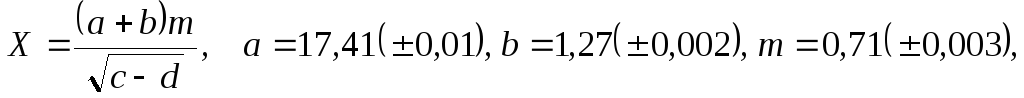
 в)
в)
а)
 б)
б)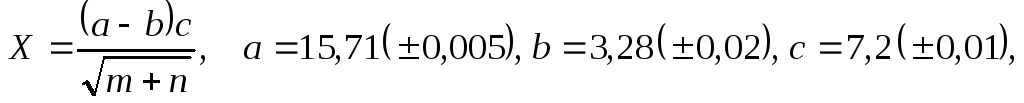
 в)
в)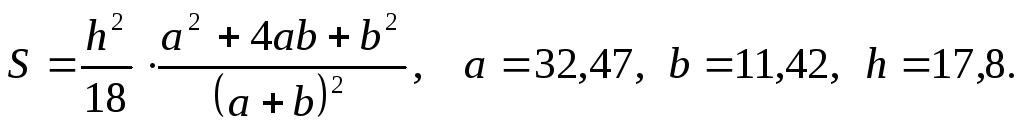
а)
 б)
б)
 в)
в)
а)
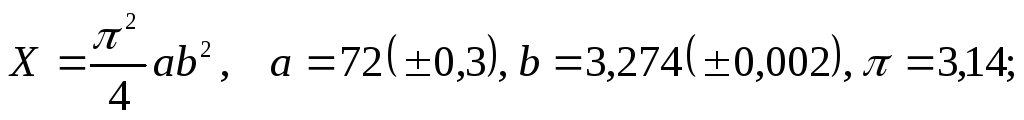 б)
б) в)
в)
а)
 б)
б)
 в)
в)
а)
 б)
б)
 в)
в) ,
где
,
где ,
,
а)
 б)
б) в)
в)
а)
 ;
б)
;
б)
 ;
в)
;
в) .
.а)
 ;
б)
;
б)
 в)
в)
а)
 б)
б)
 в)
в)
а)
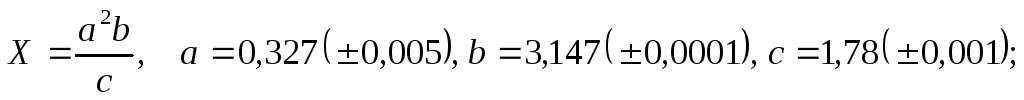 б)
б)
 в)
в)
а)
 б)
б)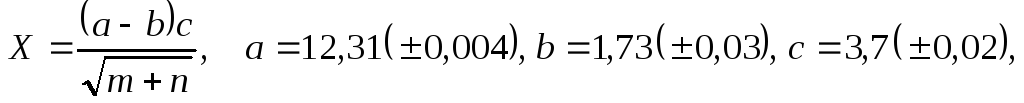
 в)
в)
а)
 б)
б)
 в)
в)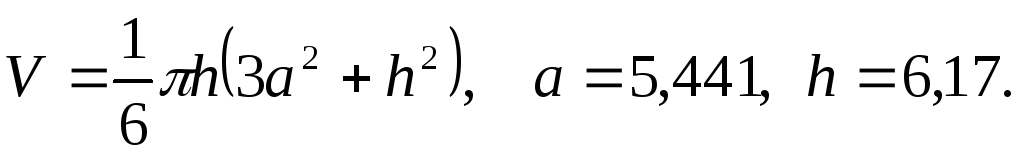
а)
 б)
б) в)
в)
а)
 б)
б)
 в)
в)
а)
 б)
б)
 в)
в) ,
где
,
где ,
,
а)
 б)
б) в)
в)
Пример 1.
Вычислить ![]() ,
где
,
где ![]() .
Определить погрешность результата.
.
Определить погрешность результата.
Решение.
При вычислении промежуточных
результатов будем сохранять одну
«запасную цифру», т.е. если по общему
правилу следует оставить ![]() значащих цифр, то в промежуточных
результатах сохраним
значащих цифр, то в промежуточных
результатах сохраним ![]() цифру. Тогда:
цифру. Тогда:
1) ![]()
При возведении приближенного
числа в степень в результате следует
оставить столько верных значащих цифр,
сколько верных значащих цифр содержится
в основании степени. Т.к. в основании
степени ![]() содержится три верных значащих цифры,
то в результате оставляем четыре цифры
(одну «запасную»).
содержится три верных значащих цифры,
то в результате оставляем четыре цифры
(одну «запасную»).
2) ![]()
При извлечении корня ![]() -й
степени из приближенного числа, в
результате следует брать столько
значащих цифр, сколько верных значащих
цифр имеет подкоренное выражение. Т.к.
в подкоренном выражении
-й
степени из приближенного числа, в
результате следует брать столько
значащих цифр, сколько верных значащих
цифр имеет подкоренное выражение. Т.к.
в подкоренном выражении ![]() содержится четыре верных значащих
цифры, то в результате оставляем пять
верных значащих цифр (одна «запасная»).
содержится четыре верных значащих
цифры, то в результате оставляем пять
верных значащих цифр (одна «запасная»).
3) ![]()
Т.к. в основании степени
![]() содержится три верных значащих цифры,
то в результате оставляем четыре цифры
(одну «запасную»).
содержится три верных значащих цифры,
то в результате оставляем четыре цифры
(одну «запасную»).
4) ![]()
В результате оставлено
три значащих цифры, т.к. наименьшее число
значащих цифр в числах ![]() равно трем.
равно трем.
5) Находим предельную
относительную погрешность, используя
правила и определения: а) предельная
относительная погрешность произведения
равна сумме предельных относительных
погрешностей сомножителей; б) предельная
относительная погрешность частного
равна сумме предельных относительных
погрешностей делимого и делителя; в)
предельная относительная погрешность
![]() -й
степени приближенного числа в
-й
степени приближенного числа в ![]() раз больше предельной относительной
погрешности самого числа; г) предельная
относительная погрешность корня
раз больше предельной относительной
погрешности самого числа; г) предельная
относительная погрешность корня ![]() -й
степени в
-й
степени в ![]() раз меньше предельной относительной
погрешности подкоренного выражения;
д)
раз меньше предельной относительной
погрешности подкоренного выражения;
д) ![]() ;
е)
;
е) ![]() . Таким образом:
. Таким образом:
![]()
6) Находим предельную абсолютную
погрешность: ![]()
Ответ: ![]() .
.
Пример 2.
Вычислить ![]() ,
где
,
где ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Определить погрешность результата.
.
Определить погрешность результата.
Решение.
1) ![]()
При сложении приближенных
чисел в результате следует сохранить
столько десятичных знаков, сколько их
в приближенном данном с наименьшим
числом десятичных знаков. При вычислении
промежуточных результатов следует
сохранить на одну цифру больше. Поэтому
при сложении чисел ![]() и
и ![]() сохраняем две цифры после запятой.
сохраняем две цифры после запятой.
![]()
Полную погрешность находим как сумму абсолютных величин всех видов погрешностей.
2) ![]()
При вычитании приближенных
чисел в результате следует сохранить
столько десятичных знаков, сколько их
в приближенном данном с наименьшим
числом десятичных знаков. При вычислении
промежуточных результатов следует
сохранить на одну цифру больше. Поэтому
при вычитании чисел ![]() и
и ![]() сохраняем три цифры после запятой.
сохраняем три цифры после запятой.
![]()
Полную погрешность находим как сумму абсолютных величин всех видов погрешностей.
3)
![]()
При возведении приближенного
числа в квадрат в результате следует
сохранить столько значащих цифр, сколько
их в основании степени. При вычислении
промежуточных результатов следует
сохранить на одну цифру больше. Поэтому
при вычислении ![]() сохраняем пять значащих цифр.
сохраняем пять значащих цифр.
При умножении и делении в результате следует сохранить столько значащих цифр, сколько их в приближенном данном с наименьшим числом верных значащих цифр. Поэтому результат округляем до двух значащих цифр.
4) Относительная погрешность:
![]() .
.
5) Абсолютная погрешность:
![]() .
.
Ответ: ![]() .
.
Пример 3.
Пользуясь правилами подсчета цифр,
вычислить ![]() ,
где
,
где ![]() .
.
Решение.
![]()
![]() .
.
Ответ:
![]() .
.
При вычислениях используем правила:
При вычислениях промежуточных результатов следует сохранять на одну цифру больше, чем рекомендуют правила сложения, вычитания, умножения и деления приближенных чисел.
При делении в результате следует сохранить столько значащих цифр, сколько их в приближенном данном с наименьшим числом верных значащих цифр. Поэтому
 ,
т.к. в числе
,
т.к. в числе  три значащих цифры (+ одна «запасная»
цифра).
три значащих цифры (+ одна «запасная»
цифра).При вычитании приближенных чисел в результате следует сохранить столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков. Поэтому
 ,
т.к. наименьшее число десятичных знаков
в числе 23,67 равно двум (+ одна «запасная»
цифра).
,
т.к. наименьшее число десятичных знаков
в числе 23,67 равно двум (+ одна «запасная»
цифра).При возведении приближенного числа в квадрат в результате следует сохранить столько значащих цифр, сколько их в основании степени. Поэтому
 ,
т.к. в основании степени три значащих
цифры (+ одна «запасная» цифра).
,
т.к. в основании степени три значащих
цифры (+ одна «запасная» цифра).При умножении в результате следует сохранить столько значащих цифр, сколько их в приближенном данном с наименьшим числом верных значащих цифр. Поэтому
 ,
т.к. в каждом числе четыре значащих
цифры (+ одна «запасная» цифра).
,
т.к. в каждом числе четыре значащих
цифры (+ одна «запасная» цифра).В окончательном результате «запасная» цифра отбрасывается. И т.к. меньшее число значащих цифр сомножителей равно трем (в числе 11,8), то в результате оставляем три значащих цифры.
