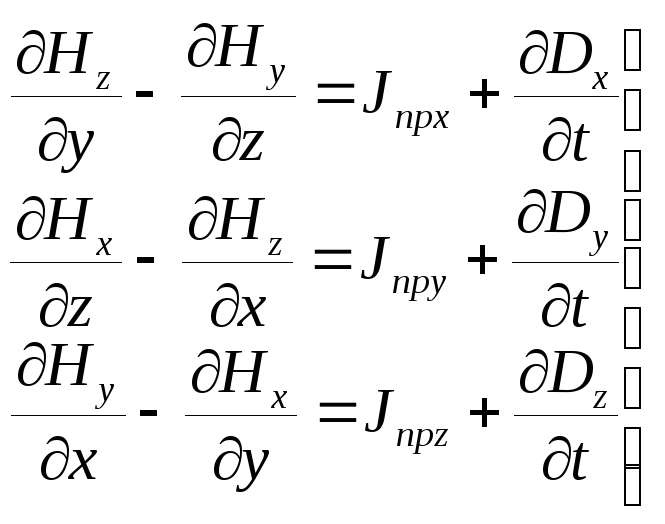1.3. Ток проводимости и ток смещения

Током проводимости называется движение носителей электрических зарядов под действием электрического поля.

Для выяснения особенностей протекания тока проводимости в объемных телах рассмотрим проводящее тело в виде бесконечного слоя (рис. 1.5). К этому телу подведены два точечных электрода, соединенные с источником. Ток внутри вещества сконцентрируется вблизи кратчайшего расстояния между электродами, однако меньшая его часть ответвится в глубь тела.

Для описания состояния такой системы необходимо знать скорость и направление движения носителей заряда в каждой точке области протекания тока внутри тела. Для этого вводится понятие плотности тока проводимости. Вектор плотности тока проводимости описывается следующим образом:

(1.18)

где		- количество носителей заряда в единице объема вещества;
	q	- заряд носителя, Кл;
	v	- вектор скорости движения носителей заряда, м/с.

Плотность тока проводимости является мерой тока, протекающего через единичную площадку, перпендикулярную вектору скорости движения носителей. Скорость носителей и плотность тока проводимости пропорциональны напряженности электрического поля:

(1.19)

где

σ

- электропроводность среды, См/м.

Электропроводность является коэффициентом пропорциональности между векторами плотности тока проводимости и напряженности электрического поля.

Формула (1.19) также относится к материальным уравнениями называется закономОма в дифференциальной форме.

Лучшими проводниками являются металлы. Максимальную электропроводность имеет серебро - 6.1*10⁷См/м. У меди она равна 5.7*10⁷См/м, а у алюминия - 3.2*10⁷См/м.

Если мы имеем дело с электрическим полем, постоянным во времени, тока проводимости достаточно. Однако в переменном поле только он не позволяет описать всю совокупность наблюдаемых явлений.

Рассмотрим цепь переменного тока с конденсатором. Переменный ток протекает между обкладками конденсатора и в том случае, когда между ними вакуум, то есть образо­вание тока проводимости невозможно. Соединительный провод, по которому течет ток проводимости, окружен кольцевыми линия­ми магнитного поля, которые как бы образуют «оболочку» вокруг него. Максвелл предположил, что эта «оболочка» не об­рывается у пластин конденсатора. Значит, переменное электрическое поле, так же как и ток проводимости, сопровождается появлением магнитного поля. Это дало Максвеллу основание для введения понятия тока сме­щения. Плотность тока смещения описывается формулой:

(1.20)

Природу тока смещения можно определить следующим образом. Всякое изменение электрического поля приводит к возникновению тока смещения.

Величина тока смещения прямо пропорциональна скорости изменения электрического поля.

2. Основные уравнения электродинамики

2.1. Первое уравнение Максвелла

Первое уравнение Максвелла является обобщением открытого Ампером закона полного тока. Ампер сформулировал этот закон следующим образом: циркуляция вектора напряженности магнитного поля по замкнутому контуру равна току, пронизывающему контур:

(2.1)

где	L – замкнутый контур,
	dl – векторный дифференциал длины контура: dl = l0dl,
	l0 – орт дифференциала длины контура,
	J – вектор плотности тока, пронизывающего контур,
	S - произвольная поверхность, опирающаяся на контур L,
	dS - векторный дифференциал поверхности: dS = n0dS,
	n0 - орт нормали к поверхности S, образующий с направлением обхода контура правовинтовую систему.

Форма замкнутого контура L может быть произвольной.

Под током, пронизывающим контур, Ампер понимал только ток проводимо­сти, что справедливо для постоянного во времени поля. В переменном поле необходимо учесть введенный Максвеллом ток смещения. При этом формула (2.1) примет вид:

(2.2)

Уравнение (2.2) записано для контура конечных размеров и называется первым уравнением Максвелла в интегральной форме.

К дифференциальной форме первого уравнения перейдем с помощью теоремы Стокса (формула (1.34), [6]). Она позволяет заменить циркуляцию векто­ра Н по контуру L интегралом от rot Н по поверхности S, опирающейся на этот контур:

(2.3)

Так как поверхность S выбрана произвольно, то равенство (2.3) может быть удовлетворено только в случае равенства подынтегральных выражений:

(2.4)

Равенство (2.4) называется первым уравнением Максвелла в дифференциальной форме. Это векторное уравнение эквивалентно трем скалярным уравне­ниям. В декартовой системе координат х, у, z они примут следующий вид:

(2.5)

Аналогичные уравнения в других системах координат могут быть получены с помощью формул перехода (2.5) – (2.7) или (2.11) – (2.13) [6].