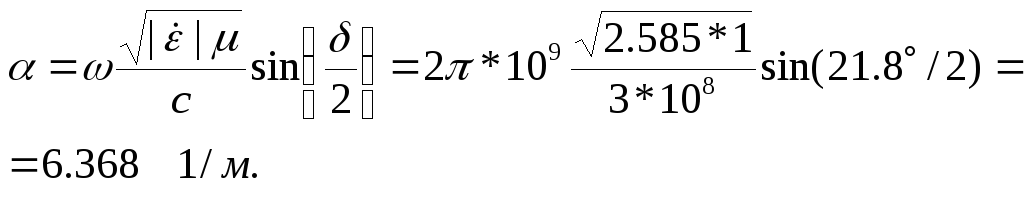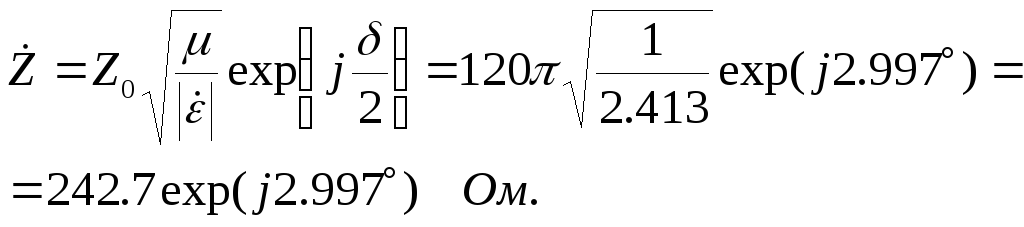8. Примеры решения задач

8.1. Электромагнитная волна частотой 1 ГГц распространяется в среде с относительной диэлектрической проницаемостью ε = 2,4, тангенсом угла диэлектрических потерь tg δ = 0.4 и относительной магнитной проницаемостью μ = 1. Рассчитать фазовую скорость, длину и коэффициент затухания волны, а также волновое сопротивление и затухание волны на пути в 1 м.

Решение.Формула для фазовой скорости имеет номер (5.15):

(5.15)

Для того чтобы воспользоваться этой формулой, надо вычислить модуль комплексной относительной диэлектрической проницаемости и угол потерь. Модуль комплексной относительной диэлектрической проницаемости рассчитывается по формуле (5.7):

(5.7)

Угол потерь: δ = arctg (0.4) = 21.8˚.

Получим следующую величину фазовой скорости:

Длина волны:

Волновое сопротивление вычисляется по формуле (5.16):

(5.16)

Коэффициент затухания вычисляется по формуле (5.10):

(5.10)

Затухание волны вычисляется по формулам (5.12) - (5.14):

	(5.12)
Нп.	(5.13)
	(5.14)

Ответ. v_ф = 1.9*10⁸ м/с, λ = 0.19 м, Z = 234.5exp(j10.9˚), α = 6.368 1/м, L = 582.9 = 6.368 Нп = 55.31 дБ.

8.2.Плоская электромагнитная волна частотой 1 ГГц распространяется в среде с относительной диэлектрической проницаемостью ε = 2,4, электропроводностью σ = 0.014 См/м и относительной магнитной проницаемостью μ = 1. Рассчитать фазовую скорость, длину и коэффициент затухания волны, а также волновое сопротивление и затухание волны на пути в 5 м.

Решение.По формуле (5.1) рассчитываетсяtgδ:

(5.1)

По формуле (5.7) рассчитывается модуль комплексной относительной диэлектрической проницаемости:

(5.7)

Угол потерь: δ = arctg0.105 = 5.994˚.

Фазовая скорость вычисляется по формуле (5.15):

(5.15)

Длина волны – это путь, который она проходит за период:

Волновое сопротивление вычисляется по формуле (5.16):

(5.16)

Коэффициент затухания рассчитывается по формуле (5.10):

(5.10)

Затухание волны вычисляется по формулам (5.12) - (5.14):

	(5.12)
Нп.	(5.13)
	(5.14)

Ответ. v_ф = 1.934*10⁸ м/с, λ = 0.1934 м, Z = 242.7exp(j2.997˚), α = 1.701 1/м, L = 4939 = 8.505 Нп = 73.87 дБ.

8.3. Плоская электромагнитная волна частотой 10 МГц распространяется в металле с параметрами σ = 5*10⁷ См/м, μ = 1. Вычислить фазовую скорость, коэффициент затухания и глубину проникновения поля.

Решение.Фазовая скорость вычисляется по формуле (5.27)

(5.27)

Коэффициент затухания рассчитывается по формуле (5.26):

(5.26)

Глубина проникновения вычисляется по формуле (5.28):

(5.28)

Ответ: v_фм= 1.414*10³м/с, α_м= 4.443*10⁴1/м,d= 2.251*10^-5м.

8.4.Плоская электромагнитная волна частотой 30 МГц распространяется в средах, электродинамические характеристики которых приведены в таблице 8.1.

Таблица 8.1
№ среды	1	2	3	4	5	6
ε	1	0	1	1	4	4
σ,См/м	4	0	0.001	0.01	0.001	0.01

Рассчитать расстояние, на котором фаза волны изменится на угол φ₁ = 270° и на угол φ₂ = 2520°.

Решение. За изменение фазы волны отвечает коэффициент фазы. Его величина равна изменению фазы в радианах при прохождении 1 метра пути. Значит, расстояние, при прохождении которого фаза волны изменяется на некоторый угол, может быть определено делением этого угла на коэффициент фазы:

(8.1)

где l- расстояние, м; φ - сдвиг фазы на расстоянии l, рад; β- коэффициент фазы, рад.

В общем случае коэффициент фазы определяется по формуле (5.9):

(5.9)

Эта формула дает результат в радианах. Значит, сдвиг фазы надо перевести из градусов в радианы по формуле:

(8.2)

Получим: φ₁ = 4.712 рад, φ₂ = 43.98 рад.

В вакууме, при ε = 1 и σ = 0 См/м получим:

В диэлектрике с ε = 4 и σ = 0 См/м получим:

В диэлектрике с потерями с ε = 1 и σ = 0.001 См/м.

Для расчета коэффициента фазы в этой среде надо предварительно по формуле (5.1) найти tg δ:

(5.1)

Угол потерь δ = 30.96˚.

Модуль комплексной относительной диэлектрической проницаемости необходимо вычислить по формуле (5.7):

(5.7)

Коэффициент фазы:

Расстояния l₁ и l₂:

В диэлектрике с потерями с ε = 1 и σ = 0.01 См/м.

Угол потерь δ = 80.54˚.

Коэффициент фазы:

Расстояния l₁ и l₂:

В диэлектрике с потерями с ε = 4 и σ = 0.001 См/м.

Угол потерь δ = 8.531˚.

Коэффициент фазы:

Расстояния l₁ и l₂:

В диэлектрике с потерями с ε = 4 и σ = 0.01 См/м.

Угол потерь δ = 56.31˚.

Коэффициент фазы:

Расстояния l₁ и l₂:

Ответ:

Таблица 8.2
№ среды	1	2	3	4	5	6
l1, м	7.5	3.75	7.206	3.986	7.479	5.878
l2, м	70	35	67.26	37.22	69.81	54.86

8.5. Плоская электромагнитная волна частотой 10 ГГц распространяется вдоль оси z. В плоскости z = 0 амплитуда вектора напряженности электрического поля описывается соотношением Е = (х₀0.5 + у₀0.2) В/м. Рассчитать амплитуду вектора напряженности магнитного поля Н в плоскости z = 0, а также мгновенные значения векторов Е и Н и плотность потока энергии в плоскости z = 10 см в вакууме (среда 1), немагнитном диэлектрик с ε = 4 (среда 2) и немагнитном диэлектрике с потерями с ε = 4 и σ = 0.01 См/м (среда 3).

Решение.В общем случае комплексные амплитуды векторов напряженности электрического и магнитного полей связаны между собой волновым сопротивлением. Для выполнения расчетов нами были получены формулы (4.10) и (4.11), относящиеся к волне, распространяющейся вдоль осиz:

(4.10)

(4.11)

Для расчета волнового сопротивления среды надо воспользоваться формулой (5.16):

(5.16)

Волновое сопротивление вакуума Z₀= 120πОм мы определили в формуле (5.7). Следовательно, проекции вектора напряженности магнитного поля на оси координат в вакууме будут равны:

Н= (-х₀5.306 +у₀13.26) *10^-4 А/м.

Для немагнитного диэлектрика с ε = 4 получим:

Н= (-х₀1.061 +у₀2.653) *10^-3 А/м.

Для расчета волнового сопротивления немагнитного диэлектрика с потерями при ε = 4 и σ = 0.01 См/м надо по формуле (5.7) найти модуль относительной диэлектрической проницаемости:

(5.7)

Для того чтобы воспользоваться этой формулой, надо по формуле (5.1) найти tg δ. Получим:

(5.1)

Угол потерь δ = 2.577˚.

Модуль комплексной относительной диэлектрической проницаемости:

Волновое сопротивление:

Модули составляющих вектора напряженности магнитного поля:

В отличие от сред 1 и 2 волновое сопротивление диэлектрика с потерями является комплексным, то есть имеет не только модуль, но аргумент 1.289°. Это необходимо учесть при записи выражения для вектора Н. Но предварительно надо аргумент волнового сопротивления перевести в радианы по формуле (8.2):

(8.2)

Аргумент волнового сопротивления имеет знак +, значит, аргумент вектора напряженности магнитного поля будет отрицательным:

Таким образом, амплитуды векторов напряженности электрического Е и магнитного Н полей в плоскости z = 0 определены. Для описания мгновенных значений этих векторов надо учесть зависимость поля от расстояния и времени. В общем случае для этого надо амплитуды умножить на экспоненты с соответствующими показателями степени, а затем взять действительную часть результата. Эту процедуру мы проделаем для среды 3, в которой есть потери.

Для сред без потерь можно поступить проще. Вначале по формуле (5.9) рассчитаем коэффициенты фазы:

(5.9)

Получим:

Среда 1	Среда 2

Общий вид выражения для мгновенного значения приведен, например, в формуле (4.3):

(4.3)

Сюда надо подставить круговую частоту и произведение βz.Получим:

Среда 1		(8.3)
		(8.4)
Среда 2		(8.5)
		(8.6)

Для среды с потерями разумней пойти стандартным путем. Общий вид исходного выражения описан, например, формулой (4.1):

(4.1)

Получим

		(8.7)
Среда 3		(8.8)

В общем случае комплексное волновое число рассчитывается по формуле (3.4)

(3.4)

где β вычисляется по формуле (5.9), а α – по формуле (5.10)

(5.10)

Получим:

Среда 3

В среде с потерями необходимо учесть уменьшение амплитуды напряженности поля за счет потерь. Для этого надо воспользоваться следующей формулой:

(8.9)

где А₀- амплитуда напряженности поля при z = 0; А - амплитуда напряженности поля при z = z₁.

Получим:

(8.10)

На эту величину надо умножить амплитуды составляющих поля. Получим:

Среда 3		(8.11)
		(8.12)

Для определения плотности потока энергии в плоскости z = 0.1 м необходимо вычислить вектор Пойнтинга – векторное произведение векторов Е и Н. В этой задаче вектор Пойнтинга можно найти несколькими способами. Во-первых, можно из проекций на оси координат сформировать амплитуды векторов напряженности электрического и магнитного полей и перемножить их векторно в соответствии с формулой (7.1):

(7.1)

где	П	- вектор Пойнтинга, Вт/м2;
	Е	- амплитуда вектора напряженности электрического поля, В/м;
	Н	- амплитуда вектора напряженности магнитного поля, А/м.

При вычислении вектора Пв среде с потерями надо произведение амплитуд умножить на косинус сдвига фаз между векторами напряженности электрического и магнитного полей.

Возможен и другой путь, вероятно, более простой. Волна распространяется вдоль оси z, значит, ориентация вектора Пойнтинга определена заранее. Осталось определить его модуль

Для этого надо перемножить проекции векторов напряженности электрического и магнитного полей на разноименные оси: Е_х умножить на Н_у, а Е_у – на Н_х, а результаты сложить. Для сред без потерь эту процедуру в общем виде можно описать следующим соотношением:

(8.13)

Получим:

Среда 1		(8.14)
Среда 2		(8.15)

Для среды с потерями надо, кроме того, произведение амплитуд проекций умножить на косинус сдвига фаз между векторами напряженности поля. Получим:

Среда 3

(8.16)

Ответ:

Среда 1
Среда 2
Среда 3

8.6. Определить комплексную амплитуду вектора напряженности электрического поля плоской электромагнитной волны, распространяющейся в направлении оси z, в металле с параметрами σ = 6*10⁷ См/м, μ = 1 на частотах 10 кГц и 1 МГц, если в заданной точке пространства комплексная амплитуда вектора напряженности магнитного поля Н = y₀ 25 А/м.

Решение. Для того чтобы рассчитать комплексную амплитуду вектора напряженности электрического поля, надо по формуле (5.28) найти волновое сопротивление металла:

(5.28)

Далее надо воспользоваться следующей формулой:

(8.17)

Получим на частоте 1 МГц:

На частоте 10 кГц:

8.7. Вывести формулу для определения уменьшения амплитуды поля плоской электромагнитной волны на пути, равном длине волны в среде с потерями. Во сколько раз уменьшится амплитуда поля на указанном расстоянии в среде с параметрами ε = 2, μ = 1, σ = 10^-4 См/м на частоте 10 МГц?

Решение.Затухание плоской волны при распространении в среде с потерями описывается формулой (5.12):

(5.12)

Вместо z сюда надо подставить λ.

Для коэффициента затухания в среде с потерями есть формула (5.10):

(5.10)

Длину волны через параметры среды можно выразить с помощью формулы (1.6):

(1.6)

Отсюда

(8.18)

Осталось (5.9) найти β:

(5.9)

Теперь надо подставить α, β и λ в формулу (5.12). Получим:

(8.19)

Формула готова. Осталось по формуле (5.1) найти угол потерь tg δ. Получим:

(5.1)

L = 1.76 раза.

Ответ:1.76 раза.

8.8. Определить толщину медного экрана, который обеспечивает ослабление амплитуды электромагнитного поля в 10⁴ раза на частотах 50 Гц и 50 МГц.

Решение.Вначале надо по формуле (5.10) найти коэффициент затухания:

(5.10)

Уменьшение напряженности поля при распространении в среде с потерями описывается формулой (5.12).

(5.12)

Но нам надо найти толщину экрана zпо заданному затуханию. Следовательно, надо взять натуральный логарифм отL= 10⁴и разделить результат на коэффициент затухания. Получим:

Для 50 Гц z= 86.83 мм. Для 50 МГцz= 86.83 мкм.

Ответ. 86.83 мм приf= 50 Гц, 86.83 мкм приf= 50 МГц.

Приложение 1