
2 Метод главных компонент
Для решения трехклассовой задачи классификации объектов, требуется свести эту задачу к поэтапному решению двухклассовых задач. На первом этапе идентифицируются объекты 1 класса (ФЖ – трепетание и фибрилляция желудочков), а объекты, принадлежащие двум другим классам, временно объединяются как 2-ой общий класс (НР+ЖТ – нормальный фоновый ритм и желудочковая тахикардия). Если классифицируемый объект не принадлежит классу 1, то помещается во второй этап классификации, в котором определяется принадлежность к одному из двух оставшихся классов – нормальному фоновому ритму (НР) или желудочковой тахикардии (ЖТ). Изображение трех классов в пространстве первых двух главных компонент представлено на рисунке 3.
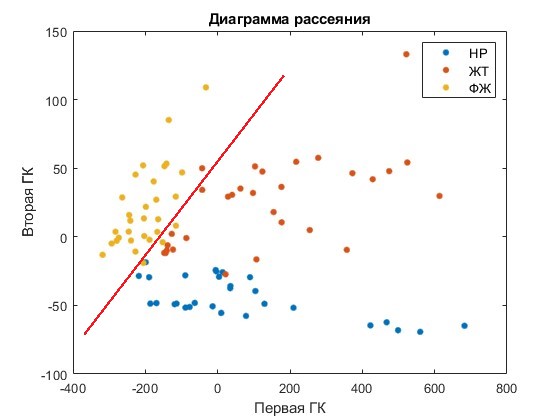
Рисунок 3 – Объекты в пространстве двух первых главных компонент
Доля дисперсии первых двух главных компонент составляет 93,06 % и 2,80 % соответственно. На первом этапе было решено выделить особо опасный класс нарушений ритма сердца – трепетание и фибрилляция желудочков (ФЖ). Элементы этого класса обладают наименьшей дисперсией и легко линейно разделимы, как показано на рисунке 3.
3 Метод классификации по минимуму расстояния
Для
того, чтобы провести классификацию по
минимуму расстояния необходимо определить
весовой вектор
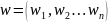 ,
пронормировать этот вектор
,
пронормировать этот вектор
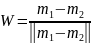 ,
сделав его единичным вектором, и
спроецировать точки обоих классов на
прямую линию, определяемую положением
W.
На этом этапе также будет полезно
построить одномерные гистограммы двух
классов. Порог классификации
,
сделав его единичным вектором, и
спроецировать точки обоих классов на
прямую линию, определяемую положением
W.
На этом этапе также будет полезно
построить одномерные гистограммы двух
классов. Порог классификации
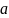 выбирается в соответствии с формулой
(1).
выбирается в соответствии с формулой
(1).
|
(1) |
где
 и
и
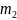 – средние значения первого и второго
классов, соответственно;
– средние значения первого и второго
классов, соответственно;
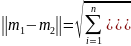 – евклидова норма.
– евклидова норма.
Разделяющая
гиперплоскость определяется как
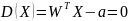 и ей соответствует следующий алгоритм
распознавания:
и ей соответствует следующий алгоритм
распознавания:
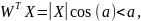 то
класс 1;
то
класс 1;
 то
класс 2.
то
класс 2.
Т.е. процедура распознавания заключается в вычислении проекции вектора X на направление весового вектора W и сравнении полученной величины с порогом a (см. рисунок 4).
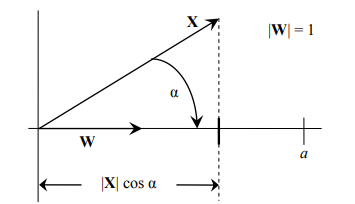
Рисунок 4 – Проекция на весовой вектор
Ниже представлены гистограммы и соответствующие им огибающие, построенные по распределению Гаусса, для первого этапа (рисунок 5) и для второго этапа (рисунок 6). На первом этапе классифицируются объекты, принадлежащие к первому классу (ФЖ – трепетание и фибрилляция желудочков), на втором этапе дифференцируются оставшиеся два класса – нормы (НР) и желудочковой тахикардии (ЖТ).
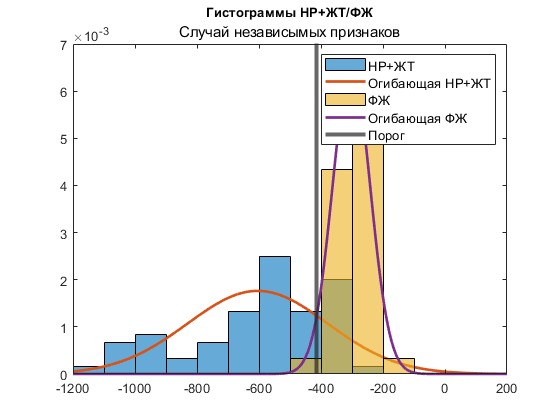
Рисунок 5 – Классификация по минимуму расстояния НР+ЖТ / ФЖ
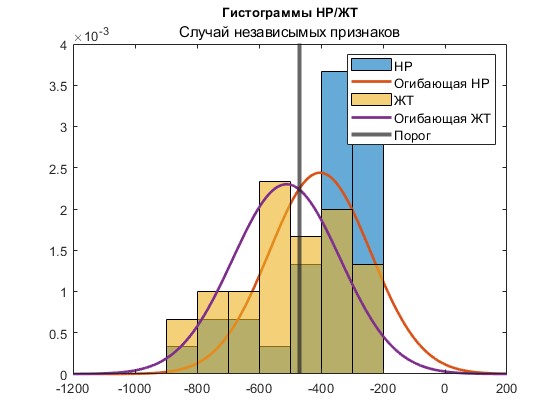
Рисунок 6 – Классификация по минимуму расстояния НР / ЖТ
Оценим получившие средние выборочные и дисперсию классов в таблице 3.
Таблица 3 – Среднее и дисперсии проекций
Этап классификации |
Класс |
Среднее |
Дисперсия |
Этап 1 (проекции на вектор W1) |
ФЖ |
-302.00 |
3.76
|
НР + ЖТ |
-604.00 |
51.22 103 |
|
Этап 2 (проекции на вектор W2) |
НР |
– 403.00 |
26.74 103 |
ЖТ |
– 511.13 |
30.08 103 |
Запишем получившиеся коэффициенты весового вектора и соответствующие им пороги классификации.
ФЖ / НР+ЖТ: W1 = [-0.96; -0.06; -0.11; 0.02; 0.11; -0.06; -0.08; -0.05; -0.06; -0.06; -0.04; -0.04; -0.05; -0.04; -0.03] при a = – 415;
НР / ЖТ: W2 = [-0.62; -0.26; -0.45; -0.50; -0.18; - 0.07; -0.15; -0.08; -0.04; -0.01; -0.01; 0.01; 0.04; 0.04; 0.05] при a = – 470;
Несмотря на то, что порог был вычислен по формуле (1), было решено уточнить это значение исходя из визуальной оценки получившихся гистограмм и их огибающих, чтобы повысить точность классификации.
Запишем уравнения дискриминантной функции.
ФЖ
/ НР+ЖТ:
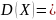 –
0.96(x1)
– 0.06(x2)
– 0.11(x3)
+ 0.02(x4)
+ 0.1(x5)
– 0.06(x6)
– 0.08(x7)
– 0.05(x8)
– 0.06(x9)
– 0.06(x10)
– 0.04(x11)
– 0.04(x12)
– 0.05(x13)
– 0.04(x14)
– 0.03(x15)
+ 415 = 0;
–
0.96(x1)
– 0.06(x2)
– 0.11(x3)
+ 0.02(x4)
+ 0.1(x5)
– 0.06(x6)
– 0.08(x7)
– 0.05(x8)
– 0.06(x9)
– 0.06(x10)
– 0.04(x11)
– 0.04(x12)
– 0.05(x13)
– 0.04(x14)
– 0.03(x15)
+ 415 = 0;
НР / ЖТ: – 0.62(x1) – 0.26(x2) – 0.45(x3) – 0.50(x4) – 0.18(x5) – 0.07(x6) – 0.15(x7) – 0.08(x8) – 0.04(x9) – 0.01(x10) – 0.01(x11) + 0.01(x12) + 0.04(x13) + 0.04(x14) + 0.05(x15) + 470 = 0;
Получив
скалярную проекцию на весовой вектор
W
и вычтя пороговое значение
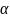 ,
применяем следующие решающие правила:
,
применяем следующие решающие правила:
Если
 ,
то данный объект принадлежит классу
ФЖ, иначе объект принадлежит объединённому
классу НР+ЖТ и переходит на второй этап
классификации. На втором этапе снова
сверяем, если
,
то данный объект принадлежит классу
ФЖ, иначе объект принадлежит объединённому
классу НР+ЖТ и переходит на второй этап
классификации. На втором этапе снова
сверяем, если
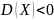 ,
то данный объект принадлежит классу
ЖТ, иначе НР.
,
то данный объект принадлежит классу
ЖТ, иначе НР.
Проведем оценку точности, чувствительности и специфичности алгоритма классификации по минимуму расстояний (см. таблица 4 и 5), а также построим ROC-кривые (рисунок 7).
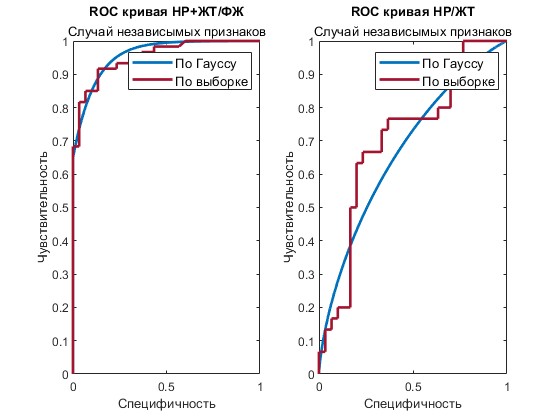
Рисунок 7 – ROC кривые по гистограммам и оценкам Гаусса для первого этапа классификации (слева) и для второго (справа)
Чувствительность
–
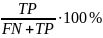 ;
;
Специфичность
–
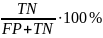 ;
;
Точность
–
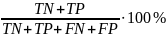 ;
;
где TP – число правильно определенных положительных исходов, FP – число исходов, ошибочно отнесённых к положительным; TN – число правильно определенных отрицательных исходов; FN – число исходов, ошибочно отнесенных к отрицательным.
Таблица 4 – Оценка ошибок классификации по гистограммам
Этап классификации |
TP |
FP |
TN |
FN |
Чувствительность, % |
Специфичность, % |
Точность, % |
1 этап |
29 |
13 |
47 |
1 |
96.6 |
78.3 |
84.4 |
2 этап |
15 |
6 |
24 |
15 |
50.0 |
80.0 |
65.0 |
Таблица 5 – Оценка ошибок классификации по оценке распределения Гаусса
Этап классификации |
TP, % |
FP, % |
TN, % |
FN, % |
Чувствительность, % |
Специфичность, % |
Точность, % |
1 этап |
96.6 |
20.0 |
79.6 |
3.3 |
96.6 |
79.9 |
88.3 |
2 этап |
59.2 |
34.0 |
65.9 |
40.7 |
59.2 |
65.9 |
62.5 |
Вывод: при использовании метода классификации по минимуму расстояния достигнута точность 84.4 % на первом этапе и 65.0 % на втором этапе. Для гауссовского распределения точность на первом и втором этапе соответственно составили 88.3 % и 62.5 %. Пересечения классов в проекции на весовой вектор – основной фактор резкого снижения показателей точности на втором этапе классификации.

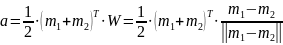
 103
103