
- •Санкт-Петербургский Государственный Электротехнический Университет «ЛЭТИ» Кафедра Биотехнических Систем
- •5.2. Методы обработки в частотной области. Частотная фильтрация
- •5.2. Методы обработки в частотной области. Частотная фильтрация
- •5.2. Методы обработки в частотной области. Частотная и пространственная фильтрация
- •5.2. Методы обработки в частотной области. Частотная и пространственная фильтрация
- •5.2. Методы обработки в частотной области. Частотная и пространственная фильтрация
- •5.2. Методы обработки в частотной области. Частотная фильтрация
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФНЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФНЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФНЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФНЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФНЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФНЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФНЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФНЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФНЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФВЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФВЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФВЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФВЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФВЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФВЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФВЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация. ФВЧ
- •5.2. Методы обработки в частотной области. Частотная фильтрация
- •5.2. Методы обработки в частотной области. Частотная фильтрация
- •5.2. Методы обработки в частотной области. Частотная фильтрация
- •5.2. Методы обработки в частотной области. Частотная фильтрация

Санкт-Петербургский Государственный Электротехнический Университет «ЛЭТИ» Кафедра Биотехнических Систем
Автоматизированный
анализ
изображений
Анна Юрьевна Виллевальде
к.т.н., доц.

5.2. Методы обработки в частотной области. Частотная фильтрация
Методы обработки изображений в частотной области применяются для выделения характерных признаков изображения; фильтрации изображений; кодирования (сжатия) или сокращения размерности при выполнении вычислений (ширина спектра уменьшается за счет отбрасывания или грубого
квантования малых по значению коэффициентов преобразования).
Частотные фильтры изменяют значения яркостей пикселей относительно периодичности и пространственного распределения изменений яркости на изображении.
Детали и острые края на изображении отражают значительные изменения яркости на коротких расстояниях и связаны с высокими пространственными частотами. Плавные изменения яркости связаны с низкими пространственными частотами.
Высокочастотные фильтры обеспечивают выделение областей резких изменений на изображении, которые соответствуют острым краям, деталям и шуму.
Низкочастотные фильтры обеспечивают усиление областей постепенных изменений на изображении, фона.
Автоматизированный анализ |
2 |
изображений |
|

5.2. Методы обработки в частотной области. Частотная фильтрация
Частотные фильтры оперируют с частотным представлением изображения;
его обычно получают с помощью прямого быстрого преобразования Фурье |
|
||||||||
(БПФ). |
БПФ |
|
Фильтр |
|
Обратное |
|
|||
|
|
|
|
|
БПФ |
|
|
||
|
f(x, y) |
F(u, v) |
F*(u, v) |
|
|
g(x, y) |
|||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
При выполнении частотной фильтрации пространственные частоты, видимые на изображении, преобразованном с помощью БПФ, отбрасываются в соответствии с выбранным методом, а затем отфильтрованное изображение восстанавливается в пространственном представлении с помощью обратного БПФ.
Основное уравнение частотной фильтрации:
где F(u,v) — БПФ исходного изображения f(x,y) размерами M×N, H(u,v) — фильтр-функция (фильтр, передаточная функция фильтра),
— обратное ДПФ, g(x,y) — результат фильтрации (выходное изображение).
F, H, g — массивы размерами M×N.
H(u,v)F(u,v) — поэлементное произведение массивов.
Удобно, если H(u,v) — функция, симметричная относительно своего центра, при этом F(u,v) также должна быть центрирована.
Автоматизированный анализ |
3 |
изображений |
|

5.2. Методы обработки в частотной области. Частотная и пространственная фильтрация
Теорема о свертке
Пусть t – пространственная область, μ — частотная область, f(t) и h(t) – непрерывные функции,
F(μ) и H(μ) — Фурье-преобразования от f(t) и h(t) соответственно. Тогда: 1. 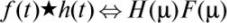
Фурье-образ свертки двух функций в пространственной области |
|
эквивалентен произведению в частотной области Фурье-образов этих двух |
|
функций. |
|
И наоборот, если имеется произведение двух Фурье-образов, можно |
|
получить |
вычисления обратного ПФ. |
свертку в пространственной |
|
2.
Свертка в частотной области аналогична умножению в пространственной области.
Автоматизированный анализ |
4 |
изображений |
|

5.2. Методы обработки в частотной области. Частотная и пространственная фильтрация
Связь между фильтрацией в пространственной и частотной областях определяется теоремой о свертке.
Пусть в частотной области задан фильтр H(u,v), требуется определить его эквивалентное представление в пространственной области.
Рассмотрим единичный импульс f(x,y)=δ(x,y), ПФ F(u,v)=1.
Тогда результат фильтрации — обратное ПФ частотного фильтра, соответствует пространственному фильтру.
Аналогично: если задан пространственный фильтр, его представление в частотной области можно получить выполнением прямого ПФ пространственного фильтра.
Т.о. два фильтра образуют Фурье-пару: h(x,y) — пространственный фильтр.
Этот фильтр м.б. получен как отклик частотного фильтра на единичный импульс, поэтому h(x,y) часто называют импульсной характеристикой (импульсным откликом) фильтра H(u,v).
При получении пространственного представления частотных фильтров (и наоборот) с помощью БПФ пространственные параметры и значения коэффициентов являются ограниченными, поэтому такие фильтры называют фильтрами с конечными импульсными характеристиками (КИХ- фильтрами).
Автоматизированный анализ |
5 |
изображений |
|

5.2. Методы обработки в частотной области. Частотная и пространственная фильтрация
Пространственная маска |
Фильтр, показанный |
Результат |
и трехмерный график ее |
в виде |
фильтрации |
частотного |
изображения |
|
представления |
|
|
Один из способов воспользоваться преимущественными свойствами каждой из областей состоит в том, чтобы задать фильтр в частотной области, вычислить его обратное БПФ и полученный полноразмерный пространственный фильтр использовать в качестве образца для построения масок пространственных фильтров меньшего размера.
Автоматизированный анализ |
6 |
изображений |
|

5.2. Методы обработки в частотной области. Частотная фильтрация
Рассмотрим фильтр:
{ =0 при u=v=0
H(u,v) =1 во всех остальных точках
Член F(u,v), соответствующий нулевой (основной) частоте u=v=0, несет информацию о постоянной составляющей и определяет среднюю яркость исходного изображения.
Фильтр H(u,v) задерживает член F(u,v), несущий информацию о постоянной составляющей, и пропускает все остальные составляющие F(u,v), т.о. средняя яркость выходного изображения будет равна нулю.
Исходное изображение Обработанное изображение
Изображение
поврежденной
интегральной
схемы, полученное при помощи сканирующего электронного микроскопа
Автоматизированный анализ |
7 |
изображений |
|

5.2. Методы обработки в частотной области. Частотная фильтрация. ФНЧ
Низкочастотный БПФ-фильтр (ФНЧ) уменьшает или удаляет высокие частоты, присутствующие в плоскости БПФ; подавляет информацию, связанную с быстрыми изменениями яркостей на изображении в пространственной области.
В результате возникает изображение, на котором шум, детали, текстура и острые края сглажены. НЧ-фильтр удаляет или ослабляет пространственные частоты, расположенные вне частотного диапазона, центрированного на основной (нулевой) частоте
.
v |
u |
a) БПФ изображения, отфильтрованного ФНЧ (высокие частоты отфильтрованы);
b) Отфильтрованное изображение (обратное БПФ спектра a)
c) БПФ изображения, отфильтрованного ФНЧ (высокие частоты отфильтрованы);
d) Отфильтрованное изображение
(обратное БПФ спектра c) Автоматизированный анализ 8
изображений

5.2. Методы обработки в частотной области. Частотная фильтрация. ФНЧ
Идеальный фильтр низких частот
Двумерный фильтр низких частот, который пропускает без затухания все частотные составляющие внутри круга радиусом D0 от начала координат и удаляет все частотные составляющие вне этого круга:
D0 — частота среза, заданная положительная константа, D(u,v) — расстояние от точки (u,v) частотной области до начала координат (центра частотного прямоугольника).
Идеальный ФНЧ является радиально симметричным вокруг начала координат, а значит, он полностью задается своим радиальным сечением (профилем).
(а) |
Трехмерный |
график |
передаточной |
функции |
идеального |
ФНЧ |
|
(б) Представление фильтра в виде изображения
(в) Радиальный профиль фильтра
Автоматизированный анализ |
9 |
изображений |
|

|
|
5.2. Методы обработки в частотной области. |
||
|
|
|
|
Частотная фильтрация. ФНЧ |
C(f) |
|
|
Идеальный фильтр низких частот |
|
|
|
|
|
|
1 |
|
|
|
(низкочастотный срез): частота f удаляется, |
|
|
|
|
если она выше частоты среза fc за счет умножения |
|
|
|
|
каждой частоты f на коэффициент C, равный 0 или |
|
|
|
|
1, в зависимости от соотношения между f и fc: |
0 |
|
|
|
если f > fc, тогда C(f) = 0, иначе C(f) = 1 |
f0 |
f |
c |
f |
|
|
|
|
|
|
БПФ исходного изображения
После низкочастотного среза с частотой среза fc = f0 + 0,2(fmax – f0)
пространственные частоты вне диапазона [f0 , fc] удаляются
(устанавливаются в 0). Часть центрального пика, которая осталась – такая же, как и на исходном изображении 10
Автоматизированный анализ
изображений
