Расстояние от точки до прямой на плоскости.

Пусть дана точка М() и прямая Ax + By +C = 0. Под расстоянием от точки М()

до прямой Ax + By +C = 0 понимается длина перпендикуляра, опущенного из точки М на данную прямую. Расстояние от точки до прямой вычисляется по формуле

Угол между прямыми на плоскости. Условие параллельности и перпендикулярности двух прямых.

l₁

l₂

γ

β

^α

180⁰ γ

Рассмотрим две прямые l₁ и l₂, пусть они заданы уравнениями

y = k₁x + b₁

y = k₂x + b₂

Угол между прямыми - острый, есть еще угол 180 -.

tg=tg()=,где (из вывода уравнения прямой с угловым коэффициентом)

Т.о угол между двумя прямыми на плоскости можно вычислить через его тангенс

Отсюда условие параллельности 0

Условие перпендикулярности не определен, т.е. = 0,

Пример 1.Составить уравнение прямой, проходящей через точку А (3;-2) под углом 30^˚ к оси ОХ.

Т.к. tg30,т.о. k. Получим y ,но прямая проходит через точку А, следовательно -2 .Отсюда b = -2 -

Получаем y -2 -

Пример 2. Составить уравнение прямой, проходящей через точки А (-5; 4), В (3;-2)

, после преобразования y = .

Пример 3. Составить уравнение двух прямых, проходящих через точку А (2;1), одна из которых параллельна прямой 3х - 2у + 2, а другая перпендикулярна той же прямой.

Перепишем уравнение прямой как уравнение с угловым коэффициентом y = .

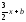Для первой (параллельной) прямой (см. условие параллельности). Тогда y = ,используем, что эта прямая проходит через точку А (2;1)

, b = -2, получим y =

Для второй прямой (перпендикулярной) 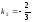(см. условие перпендикулярности). Тогда y=,используем, что эта прямая проходит через точку А (2;1), получим

, ,отсюда y = .

Пример 4. Найти расстояние между прямыми 3х + 4у - 24 = 0 и 3х + 4у + 6 = 0

Перепишем уравнения этих прямых как уравнения прямых с угловыми коэффициентами

y = ,y = .Так как их угловые коэффициенты равны, то эти прямые параллельны. Значит расстояние между этими прямыми равно расстоянию от любой точки, лежащей на одной из этих прямых, до другой прямой. Возьмем на прямой 3х + 4у - 24 = 0 произвольную точку, пусть х = 0, тогда 4у = 24 и у = 6. А (0;6). Воспользуемся формулой расстояния от точки А до прямой 3х + 4у + 6 = 0, получим

Решение задач см. книгу “Высшая математика для экономистов”//Н.Ш. Кремер глава 4 п.46., стр. 115 - 119, стр. 121 - 122, упражнения после главы 4.

Уравнение плоскости в пространстве.

M(x,y,z) M₀ (x₀,y₀,z₀)

α

Рассмотрим плоскость α, вектор - перпендикулярен плоскости α - нормаль к плоскости α. Точка М₀ (x₀,y₀,z_o) - фиксированная (данная) точка в плоскости α, М (x,y,z) - произвольная (текущая) точка в плоскости α. Тогда вектор будет перпендикулярен всем векторам , лежащим в плоскости α и начинающимся в точке М_0.

= (x - x₀, y - y₀, z - z_o). Условие перпендикулярности двух векторов - из скалярное произведение равно нулю.

Отсюда A(x - x₀) + B(y - y₀) +C(z - z_o) = 0 - (1) - уравнение плоскости α, проходящей через данную точку М₀ (x₀,y₀,z_o) перпендикулярно данному вектору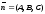

Раскроем в уравнении (1) скобки, получим Ax + By + Cz + (-Ax₀ - By₀ -Cz_o) = 0. Oбозначим D = -Ax₀ - By₀ -Cz_o,

имеем Ax + By + Cz +D = 0 - общее уравнение плоскости.

Можно доказать, что любое уравнение вида Ax + By + Cz +D = 0 задает в пространстве плоскость.

Т.к. в пространстве любая прямая может быть получена как пересечение двух непараллельных плоскостей, то общее уравнение прямой имеет вид

Две плоскости параллельны тогда и только тогда, когда параллельны их нормали, т.е. - это условие параллельности двух векторов.

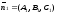
Две плоскости перпендикулярны тогда и только тогда, когда перпендикулярны их нормали, т.е. скалярное произведение равно нулю.

A₁A₂ + B₁B₂ + C₁C₂ = 0 - условие перпендикулярности плоскостей.

Угол между плоскостями в пространстве равен углу между их нормалями (легко доказать).

Таким образом