Базис и ранг системы векторов.
Определение
4.
Базисом
системы векторов
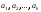называется
такая подсистема данной системы, что
она ЛНЗ и любой вектор системы является
ЛК векторов данной подсистемы.
Определение
5.
Базисом
системы векторов
называется
ее максимальная ЛНЗ подсистема
(максимальная ЛНЗ - при добавлении любого
вектора становиться ЛЗ).
Теорема 1. Определение 4 эквивалентно определению 5.
Определение 6. Рангом системы векторов называется число, равное количеству векторов в базисе данной системы.
Теорема 2. а) базис системы векторов определен неоднозначно;
б) ранг системы векторов определен однозначно.
Доказательство.
а) Рассмотрим систему векторов
=(1,1,1)
=(2,2,2)
=(1,2,0)
Векторы
и
ЛНЗ,
т.к. они не коллинеарны (см.
свойство
2˚
линейной
зависимости). Вектор
=
2
.Т.е.
,
-базис.
Аналогично
,
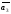ЛНЗ,
=
,т.е
,
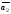-другой
базис.
б) без доказательства.
Определение 6. Элементарными называются следующие преобразования системы векторов:
поменять два вектора местами
любой вектор умножить на любое ненулевое число
к любому вектору прибавить любой другой вектор, умноженный на любое число
поменять две координаты всех векторов(у всех векторов одни и те же) местами
убрать из системы нулевой вектор
из нескольких одинаковых векторов оставить один.
Теорема 3. при элементарных преобразованиях ранг системы векторов не меняется (без доказательства).
Vι Ранг матрицы.
Рассмотрим матрицу
Обозначим ее строки
=(
,
,…,
)
=(
,
,…,
)
=(
,
,…,
)
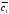Это
векторы. Можно найти базис и ранг системы
векторов - строк
,
,
.Этот
ранг называется строчечным рангом
матрицы.
Определение 1. Строчечным рангом матрицы называется количество ЛНЗ строк.
Обозначим столбцы матрицы
=(
,
,…,
)
=(
,
,…,
)
=(
,
,…,
)
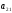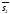Это векторы. Найдем базис и ранг данной системы векторов - столбцов.
Определение 2. Столбцевым рангом матрицы называется количество ЛНЗ столбцов.
Теорема 1. Строчечный ранг матрицы равен столбцевому (без доказательства).
Для того, чтобы найти ранг матрицы надо применить к ней элементарные преобразования системы векторов по методу Гаусса. Эти преобразования не меняют ранга системы векторов. Следовательно, в результате ранг матрицы не меняется. По окончанию преобразований мы получим, что строки матрицы образуют подсистему треугольной системы векторов, т.е. линейно независимы. Подсчитав количество оставшихся строк, мы получаем ранг матрицы.
Теорема 2. (Кронекера - Капелли). Система (S) линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы равен рангу расширенной матрицы. (без доказательства).
Из теоремы Кронекера - Капелли и метода Гаусса для решения систем линейных уравнений следует Теорема (о числе решений систем линейных уравнений).
Если
ранг основной матрицы равен рангу расширенной матрицы равен количеству неизвестных, то система имеет одно решение
если ранг основной матрицы равен рангу расширенной матрицы и меньше количеста неизвестных, то система имеет бесконечное множество решений, причем свободных переменных будет n-r, где n - число всех переменных, а r - ранг матрицы
если ранг основной матрицы не равен рангу расширенной матрицы, то система несовместна.
Пример 1. Найти ранг матрицы.
~
~
~
~
~
~
~
r = 3