V Векторы в n-мерном пространстве.

Обозначим множество всех упорядоченных наборов по n чисел. А  назовем n-мерным вектором.

Пусть , тогда (по определению)

=,

Мы определили операцию сложения векторов и операцию умножения вектора на число.

Определение 1. Вектор называется линейной комбинацией (ЛК) векторов , ,…,если существуют такие числа , что .

Определение 2. Система векторов , ,… называется линейно зависимой (ЛЗ), если существуют числане все равные 0, такие, что

Определение 3. Система векторов , ,… 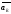называется линейно независимой (ЛНЗ), если из равенства следует, что .

Таким образом, для того, чтобы проверить зависимы или независимы данные векторы, надо составить уравнение - уравнение линейной зависимости, решить его. В случае, если нашелся ненулевой набор чисел 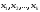, то вектора , ,…-ЛЗ, а если не нашелся ненулевой набор чисел - то ЛНЗ.

Пример 1. Выяснить, зависимы или независимы вектора

a₁=(1,1,1,1) , a₂=(2,1,-1,0), a₃=(3,3,0,0), a₄=(4,0,0,0)

Составляем уравнение линейной зависимости

()=(0,0,0,0)

=0, ==0, 3= --=0=0, 4= --2-3=0=0,т.е векторы ЛНЗ.

Пример 2. Выяснить, является система ЛЗ или ЛНЗ.

a₁=(1,2,-1,3) , a₂=(2,0,1,-1), a₃=(3,2,0,2), a₄=(5,2,1,1)

Составляем уравнение линейной зависимости

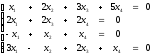
Решим систему по методу Гаусса.

Умножим второе уравнение на Ѕ, на первое место поставим третье уравнение

~ ~~

Пусть ,-свободные переменные

= --2

=+=--2+= --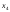

Общее решение (--;--2;;),

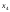
Пусть=1, =1

Частное решение (-2;-3;1;1)

Т.е. получили

Значит векторы - ЛЗ.

Свойства линейной зависимости.

1^˚. Система, состоящая из одного вектора, ЛЗ тогда и только тогда, когда этот вектор нулевой.

Доказать самостоятельно.

2^˚. Система, состоящая из двух векторов, ЛЗ тогда и только тогда, когда вектора коллинеарны (пропорциональны).

Доказать самостоятельно.

3^˚. Система векторов ЛЗ тогда и только тогда, когда хотя бы один из векторов является ЛК остальных

Доказательство. Необходимость. Пусть система векторов ЛЗ, тогда существуют числа, среди которых есть хотя бы одно ненулевое (пусть это)

Что

Отсюда

т.е. -ЛК остальных векторов.

Достаточность. Пусть один из векторов, например 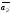, - ЛК остальных

Тогда

, следовательно (по определению) система - ЛЗ.

4^˚. Если система векторов содержит ЛЗ подсистему, то вся система ЛЗ.

Доказательство. Пусть , r<k- ЛЗ подсистема. Тогда существуют числа не все равные нулю, что . Но тогда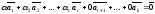. Т.к. средиeсть ненулевое число, то, по определению ЛЗ, получаем - ЛЗ.

Следствие1. Если система содержит нулевой вектор, то она ЛЗ.

Доказательство. В системе есть ЛЗ подсистема - подсистема, состоящая из одного нулевого вектора (см. 1^˚), т. е вся система ЛЗ.

Следствие 2. Если система содержит два пропорциональных вектора, то она ЛЗ.

Доказательство. Система содержит ЛЗ подсистему - два пропорциональных вектора (см. 2^˚), значит вся система ЛЗ.

Следствие 3. Если вся система ЛНЗ, то любая ее подсистема ЛНЗ.

Доказательство. Если бы какая-нибудь подсистема была ЛЗ, то вся система была бы ЛЗ, а это не так.

5^˚. Системы векторов

=()

=()

=()

………………………..

=()

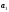(_ii0)

=()

=()

=()

=()

(_ii0)

Называются треугольными.

Треугольная система векторов ЛНЗ.

Докажем это свойство для четырех векторов

=()

=()

=()

=()

Составим уравнение линейной зависимости

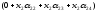+++==(0;0;0;0)

Из первого уравнения=0, но =0

Из второго уравнения (т.к. 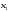=0 )=0,но =0.Из третьего уравнения (при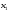== 0 )=0,но =0.Из четвертого уравнения (=0,= 0,=0)=0.Т.е вектора - ЛНЗ.

Аналогично доказывается для треугольной системы второго вида.