
- •Лекции по алгебре и математическому анализу для студентов заочного (ускоренного) обучения и вечернего (ускоренного) обучения.
- •Ι. Матрицы.
- •Свойства умножения.
- •Ιι. Определители.
- •Определители порядка 2 и 3.
- •Метод Гаусса приведения определителя к треугольному виду (посредством элементарных преобразований).
- •Ιιι Обратная матрица.
- •Явная формула обратной матрицы.
- •Нахождение обратной матрицы по методу Гаусса.
- •Ιv Системы линейных уравнений.
- •Метод Гаусса решения систем линейных уравнений - метод последовательного исключения неизвестных.
- •V Векторы в n-мерном пространстве.
- •Базис и ранг системы векторов.
- •Vι Ранг матрицы.
- •Vιι Однородные системы линейных уравнений.
- •Аналитическая геометрия. Ι Уравнение прямой на плоскости.
- •Расстояние от точки до прямой на плоскости.
- •Угол между прямыми на плоскости. Условие параллельности и перпендикулярности двух прямых.
- •Каноническое уравнение прямой в пространстве.
- •Математический анализ. Ι Геометрический смысл производной.
- •Ι Физический смысл производной.
- •Ι Определение производной.
- •Ι Неопределенный интеграл.
- •Правила интегрирования.
- •V Определенный интеграл.
Ιv Системы линейных уравнений.
Система k линейных уравнений с n неизвестными имеет вид
 (S)
(S)
где аij- коэффициенты при неизвестных х1, х2,… хn.
bi - свободные члены.
Определение 1. Решением системы (S) называется такая совокупность (упорядоченный набор или вектор) n чисел, (с1,с2, …, сn), что подставив в систему (S)место х1 - с1, вместо х2 - с2…, вместо хn - cn получим, что все уравнения системы обратились в верные числовые равенства.
Система (S) называется совместной, если она имеет решение.
Определение 2. Две системы линейных уравнений называются равносильными, если они имеют одно и то же множество решений.
Обозначим
А =
 - основная
матрица
cистемы
(S),
- основная
матрица
cистемы
(S),
X
=
 -столбец
неизвестных,
-столбец
неизвестных,
В
=
 - столбец
свободных членов.
- столбец
свободных членов.
Рассмотрим
АХ =

На основании определения равенства матриц можно систему (S) переписать в матричном виде АХ = В.
Теорема 1. Если матрица А обратима, то система АХ = В имеет единственное решение.
Доказательство.
Пусть есть 2 решения С =
 и
D
=
и
D
=
 ,тогда
АС = В и АD
= В
,тогда
АС = В и АD
= В
Следовательно, АС = АD. Домножим обе части равенства на А-1 слева получим
А-1 АС = А-1 АD, EC = ED, С = D.
Теорема
2 (правило Крамера). Пусть
в системе (S)
k
= n
(количество
уравнений
равно количеству неизвестных)
и
detA
≠ 0. Тогда
система (S)
имеет
единственное решение, которое можно
найти по формулам Крамера
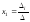 ,
где
,
где
 =
detA,
=
detA,
 получен
из
получен
из заменой
i-того
столбца столбцом свободных членов.
заменой
i-того
столбца столбцом свободных членов.
Доказательство. Т.к. detA ≠ 0? Следовательно матрица А имеет обратную А-1 . Из матричной замены системы АХ = В следует А-1 АХ = А-1 В, т.е. ЕХ = А-1 В.
Тогда
X
=

 =
=

Следовательно
x
x
Здесь

Рассмотрим определитель порядка 3 для простого вычисления
 по
формуле разложения по первому столбцу
по
формуле разложения по первому столбцу
 по
формуле
разложения
по второму столбцу
по
формуле
разложения
по второму столбцу
 по
формуле разложения по третьему столбцу.
по
формуле разложения по третьему столбцу.
Отсюда следует справедливость формул Крамера.
Единственность решения следует из теоремы 1.
Пример 1. Решить систему уравнений.

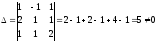
Значит можно применить формулы Крамера.

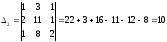


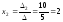

Проверка.
Подставим =4,
=4,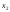 =2,
=2, =1в
систему
=1в
систему

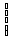 верно
верно
Ответ (4;2;1).
Метод Гаусса решения систем линейных уравнений - метод последовательного исключения неизвестных.
Определение 3. Элементарными назовем следующие преобразования системы линейных уравнений:
поменять два уравнения местами
умножить уравнение на любое ненулевое число
к любому уравнению системы прибавить любое другое уравнение системы, умноженное на любое число
поменять две переменные (одно и то же во всех уравнениях) местами
убрать из системы нулевое уравнение, т.е. уравнение вида
из нескольких одинаковых уравнений системы оставить только одно, остальные убрать.
Теорема 3. После применения элементарных преобразований к системе линейных уравнений получим систему, равносильную данной.
Теорема 4. (метод Гаусса решения систем линейных уравнений)
Любую систему (S) линейных уравнений при помощи элементарных преобразований, проведенных по методу Гаусса (см. метод Гаусса для вычисления определителей) можно привести к одному из трех следующих видов
треугольная - количество уравнений равно количеству неизвестных, в первом уравнении есть
 ,
во
втором уравнении нет
,
во
втором уравнении нет ,
но
есть
,
но
есть ,
в
третьем уравнении нет
,
в
третьем уравнении нет
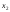 ,
но
есть
,
но
есть ,
и
т.д., в последнем уравнении есть только
,
и
т.д., в последнем уравнении есть только ,
такая
система имеет единственное решение
,
такая
система имеет единственное решение
трапециидальная - количество уравнений меньше количества неизвестных, а в остальном вид как у треугольной, в последнем уравнении несколько переменных, такая система имеет бесконечное множество решений
в системе есть “особое” уравнение - уравнение вида 0
 + 0
+ 0 +…
+0
+…
+0 =b
=b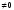 такая
система несовместна.
такая
система несовместна.
Преобразования системы линейных уравнений методом Гаусса удобно вести, осуществляя преобразования не над уравнениями, а только над коэффициентами при неизвестных и свободными членами.
Для этого рассмотрим расширенную матрицу системы.

Пример 2. решить “треугольную” систему линейных уравнений

Из
последнего уравнения
 ,из
предпоследнего
,из
предпоследнего
 .
Подставим
.
Подставим
 и
и во
второе уравнение, найдем
во
второе уравнение, найдем .
.
3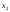 =
12+ 6
=
12+ 6 -
9
-
9 = 12 + 6
= 12 + 6 4
- 9
4
- 9 4
= 12 + 24 - 36 = 0
4
= 12 + 24 - 36 = 0
 =
0
=
0
Подставим
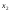 ,
,
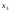 ,
, в
первое уравнение и найдем
в
первое уравнение и найдем
 .
.
 =
1 - 2
=
1 - 2 - 3
- 3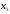 +
+ = 1 + 0 -12 +4 = -7
= 1 + 0 -12 +4 = -7
Проверка


Ответ (-7;0;4;4)
Пример 3. Решить трапециидальную систему.

Из
последнего уравнения мы можем выразить
только одно неизвестное =3-
=3- -2
-2 -
-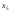 .При
этом
.При
этом
 ,
,
 ,
,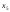 называют
свободными
переменными.
Они
принимают произвольные значения. Отсюда
и бесконечное множество решений.
называют
свободными
переменными.
Они
принимают произвольные значения. Отсюда
и бесконечное множество решений.
Из
первого уравнения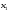 =5-
=5- +
+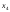 -
- .Подставим
.Подставим ,
,
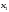 =5-3+
=5-3+ +2
+2 +
+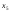 +
+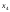 -
- =2+
=2+ +3
+3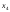 .Количество
свободных переменных определяется по
формуле n-r,
где
n
- количество
неизвестных в системе, r
- количество
оставшихся уравнений после приведения
системы к трапециидальному виду. У нас
n=5,
r=2.
5-2=3 - свободных
переменных.
.Количество
свободных переменных определяется по
формуле n-r,
где
n
- количество
неизвестных в системе, r
- количество
оставшихся уравнений после приведения
системы к трапециидальному виду. У нас
n=5,
r=2.
5-2=3 - свободных
переменных.
Общее
решение: (2+ +3
+3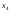 ;
3-
;
3- -2
-2 -
- ;
; ;
; ;
;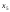 ),
),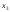 ,
, ,
,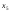

Частные
решения: (получаются из общего решения,
если вместо свободных переменных
подставить числовые значения).
 =0,
=0, =0,
=0, =1
(2;3;0;0;1)
=1
(2;3;0;0;1)
 =1,
=1,
 =1,
=1,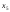 =0
(6;0;1;1;0).
=0
(6;0;1;1;0).
Пример
4.
Решить
систему уравнений.

Выпишем расширенную матрицу системы.
 ~
~ ~
~ ~
~ ~
~ ~
~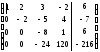 ~
~ ~
~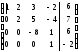
Получим треугольную систему

Из
третьего уравнения
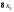 =
- 6 +
=
- 6 + = - 6 - 2 = - 8,
= - 6 - 2 = - 8, =
-1.Из
второго уравнениям
=
-1.Из
второго уравнениям = 7 - 5
= 7 - 5 + 4
+ 4 = 7 + 5 -8 = 4,
= 7 + 5 -8 = 4,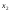 = 2.Из
первого -
= 2.Из
первого -
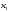 = 6 - 2
= 6 - 2 - 3
- 3 +2
+2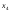 = 6 - 4 + 3 - 4 = 1
= 6 - 4 + 3 - 4 = 1
Ответ (1;2;-1;-2)
Пример 5. Решить систему.
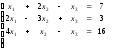
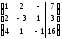 ~
~ ~
~
Получили
систему
с “особым” уравнением. Система несовместна.
Пример 6. Решить систему.

 ~
~
 ~
~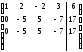 ~
~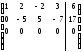 ~
~
Система имеет 4 неизвестных (n=4) и 2 уравнения r = 2. Свободных неизвестных будет
4 - 2 = 2.
Пусть ,
,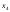 -свободные
переменные.
-свободные
переменные.
Тогда
 = -
= -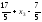
 ,подставим
в первое уравнение и выразим
,подставим
в первое уравнение и выразим

 =
-6 + 2
=
-6 + 2 - 3
- 3 - 2
- 2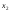 = -6 +2
= -6 +2 - 3
- 3 +
+ -
2
-
2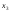 +
+
 =
=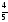 -
-

Общее
решение:
( -
-
 ;
-
;
-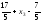
 ;
;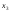 ;
; ).
).
Частные
решения
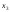 =1,
=1,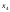 =0
(
=0
( ;
;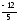 ;1;0)
;1;0)
 =1,
=1,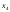 =1
(
=1
( ;
; ;1;1).
;1;1).
