
- •Лекции по алгебре и математическому анализу для студентов заочного (ускоренного) обучения и вечернего (ускоренного) обучения.
- •Ι. Матрицы.
- •Свойства умножения.
- •Ιι. Определители.
- •Определители порядка 2 и 3.
- •Метод Гаусса приведения определителя к треугольному виду (посредством элементарных преобразований).
- •Ιιι Обратная матрица.
- •Явная формула обратной матрицы.
- •Нахождение обратной матрицы по методу Гаусса.
- •Ιv Системы линейных уравнений.
- •Метод Гаусса решения систем линейных уравнений - метод последовательного исключения неизвестных.
- •V Векторы в n-мерном пространстве.
- •Базис и ранг системы векторов.
- •Vι Ранг матрицы.
- •Vιι Однородные системы линейных уравнений.
- •Аналитическая геометрия. Ι Уравнение прямой на плоскости.
- •Расстояние от точки до прямой на плоскости.
- •Угол между прямыми на плоскости. Условие параллельности и перпендикулярности двух прямых.
- •Каноническое уравнение прямой в пространстве.
- •Математический анализ. Ι Геометрический смысл производной.
- •Ι Физический смысл производной.
- •Ι Определение производной.
- •Ι Неопределенный интеграл.
- •Правила интегрирования.
- •V Определенный интеграл.
Ιιι Обратная матрица.
Обратная матрица определяется только для квадратных матриц.
Определение 1. Матрицы В называется обратной к матрице А, если АВ = ВА = Е.
Матрица, имеющая обратную, называется обратимой. Обратная матрица обозначается А-1.
Свойства обратной матрицы.
1˚. Если В обратна к А, то А обратна к В.
Доказательство этого свойства следует непосредственно из определения. Таким образом, имеем (А-1) -1 = А
2˚. Если у матрицы А есть обратная, то она единственна.
Доказательство. Пусть Х и Y - две матрицы, обратные к А. Тогда XA = AX = E и YA = AY = E.
Рассмотрим X(AY) = XE = X.
С другой стороны X(AY) = (XA)Y = EY = Y.
Следовательно Х = У.
3˚. Если матрицы А и В имеют обратные, то АВ имеет обратную, причем (АВ) -1 = В-1А-1.
Доказательство.


Явная формула обратной матрицы.
Пусть
дана матрица

Пусть
матрица А имеет ненулевой определитель.
Тогда обратную к A
матрицу
можно найти по формуле

где
 -
определитель
матрицы А,
-
определитель
матрицы А,
 -
алгебраическое
дополнение к элементам
-
алгебраическое
дополнение к элементам
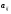 матрицы
А. Т.е.
матрицы
А. Т.е.
 =
= ,здесь
,здесь -
определитель,
полученный из определителя матрицы А
вычеркиванием i-той
строки и j-того
столбца.
-
определитель,
полученный из определителя матрицы А
вычеркиванием i-той
строки и j-того
столбца.
Доказательство формулы.
Для
того, чтобы доказать, что эта формула
задает обратную для А, необходимо
показать, что
 . Сделаем
это для матрицы порядка 3. (В общем случае
доказательство точно такое же).
. Сделаем
это для матрицы порядка 3. (В общем случае
доказательство точно такое же).

=



Здесь по главной диагонали стоит сумма произведений элементов j-того столбца на их алгебраические дополнения, тогда по теореме о разложении по любому столбцу это выражение равно определителю матрицы А. Вне главной диагонали стоит сумма произведений элементов j-того столбца на алгебраические дополнения к элементам к-того столбца (на месте kj), а это равно нулю по теореме о разложении по любому столбцу.



Применяем теорему о разложении по любой строке.
Например,
 +
+ +
+ =
0как
сумма произведений элементов первой
строки на алгебраические дополнения к
элементам второй строки,
=
0как
сумма произведений элементов первой
строки на алгебраические дополнения к
элементам второй строки,
 +
+
 +
+ =
0как
сумма произведений элементов третьей
строки на алгебраические дополнения к
элементам второй строки,
=
0как
сумма произведений элементов третьей
строки на алгебраические дополнения к
элементам второй строки,
 +
+
 +
+ =
= как
сумма произведений элементов второй
строки (на свои) на алгебраические
дополнения к элементам второй строки.
как
сумма произведений элементов второй
строки (на свои) на алгебраические
дополнения к элементам второй строки.
Теорема 1. Определитель произведения матриц равен произведению определителей.
Теорема 2. (критерий обратимости). Матрица имеет обратную тогда и только тогда, когда ее определитель отличен от нуля.
Доказательство.
Необходимость. Пусть матрица А имеет
обратную. Тогда
 .
Тогда
det
.
Тогда
det ,detE
= 1. det
,detE
= 1. det =
detA
=
detA (по
теореме1). Следовательно
(по
теореме1). Следовательно
detA =
1. Значит
detA
=
1. Значит
detA .
.
Достаточность.
Пусть определитель матрицы А отличен
от 0. Тогда

Значит обратная матрица для А существует.
Нахождение обратной матрицы по методу Гаусса.
Рассмотрим следующие преобразования матрицы А:
поменять 2 строки местами
умножить строку на ненулевое число
к любой строке прибавить другую строку, умноженную на любое число.
К матрице А порядка n припишем единичную матрицу того же порядка

Применим к матрице (А|E) метод Гаусса (аналогично тому, как описано при вычислении определителя по методу Гаусса) так, чтобы на месте матрицы А получить единичную матрицу. То, что при этом получится на месте матрицы Е, будет обратной к А. Здесь можно применять только преобразования строк.
Пример
1.
Показать,
что матрица А обратима
и найти ее обратную
обратима
и найти ее обратную
(Метод присоединения матрицы).
Вычислим
определитель detA
= 64 + 25 - 70 - 24 = -5
 0.Т.к.
определитель отличен от нуля, то А имеет
обратную, т.е. обратима.
0.Т.к.
определитель отличен от нуля, то А имеет
обратную, т.е. обратима.

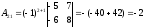
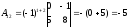







Проверка:
A

Пример2.
Решить
матричное уравнение
AX
+ B
= C ,
где
А =
,
где
А =
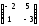 ,
,
В
=
 ,
С
=
,
С
=
 .
.
Вычислим
detC
= (-2)(-4) - (-1)(-7) = 8 - 7 = 1 0
0
detA
= (-2)(-3) – 15 = 6 - 5 = 1 0.
0.
Значит матрицы С и А - обратимы. Найдем из уравнения матрицу Х.
AX
= C -
В
-
В
А (АХ)
= А
(АХ)
= А (
C
(
C -В)
-В)
(А А)Х
= А
А)Х
= А (
C
(
C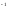 -В)
-В)
ЕХ
= А (
C
(
C -В)
-В)
Х
= А (
C
(
C -В)
-В)
Находим А-1:

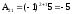
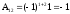


Находим C-1:
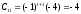

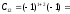


C-1-
B =

X
= A (
C
(
C - B) =
- B) =
Проверка. Подставим Х в исходное уравнение
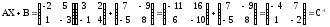
Пример 3. Найти обратную к А методом элементарных преобразований (методом Гаусса)

 ~
~
 ~
~
поменяем первую и четвертую строки меняем местами. Умножим первую строку на (-2) прибавим ко второй и четвертой, домножим первую строку на (-3) и прибавим к третьей
~ ~
~
чтобы не переходить к дробным компонентам домножим четвертую строку на (-2) и прибавим ее ко второй строке.
~ ~
~ ~
~
~
~ ~
~
Ниже главной диагонали стоят только нулевые элементы. Проведем “обратный ход” снизу вверх, чтобы получить над главной диагональю нулевые элементы.
~ ~
~ ~
~
Четвертую строку умножим на (-4) и прибавим к третьей, четвертую строку умножим на (-2) и прибавим ко второй и к первой.
~
Таким
образом


Можно сделать проверку. AА-1 должно равняться Е.
