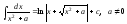Правила интегрирования.

1. 

2. 

Дополнительная таблица.

1. , -a<x<a, a>0

2. 

3. 

4. 

Чтобы доказать справедливость формул таблицы интегралов, необходимо найти производную от правой части и сравнить ее с подынтегральной функцией. Если будет совпадение, то интеграл посчитан верно.

Примеры см в книге “Высшая математика для экономистов” //Н.Ш. Кремер, гл. 10, стр. 256 - 257.

Теорема 1. Если= F(x) + c, то

Доказательство. Рассмотрим . Произведем замену переменной, пусть ax + b = t, тогда dt = d(ax + b) = (ax + b)’dx = adx, oткуда dx = .Подставим все в исходный интеграл

Замечание: если y = f(x), то dy = df(x) = f’(x)dx

Например

Пример 1.

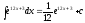
Метод замены переменной.

Пусть дан (1)

Тогда заменим и подставим в интеграл .

Пример 2.

а)

б)

в)

г) =

=

д)

V Определенный интеграл.

Пусть на отрезке [a,b] задана функция y = f(x). Разобьем отрезок [a,b] точками

x₀ = a< x₁< x₂ <… < x_n = b на n маленьких отрезков, через ∆x_i обозначим длину отрезка

[x_j-1,x_j], j=1,2…n. Пусть - произвольная точка из отрезка [x_j-1,x_j].

Вычислим f(α₁). Пусть ∆= max∆x_j, 1

Определение 1. Интегральной суммой для функции y = f(x) на отрезке [a,b] называется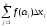

Очевидно, что интегральная сумма зависит от выбора точеки от способа разбиения отрезка [a,b] на маленькие отрезки [x_j-1,x_j]

Определение 2. Пусть при ∆→ 0 предел интегральной суммы существует, конечен и не зависит от способа выбора точекx₁,…,x_n-1 и α_1,α_2,… α_n. Тогда этот предел называется определенным интегралом от функции f(x) по отрезку [a,b], обозначается

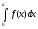
Т.е. =lim

∆→0

Таким образом, определенный интеграл – это число, в то время как неопределенный интеграл – семейство функций.

Для вычисления определенного интеграла применяется формула Ньютона – Лейбница= F(b) – F (a), где F(x) - первообразная для f(x).

Свойства определенного интеграла.

1^˚.

2^˚.

3^˚.

4^˚.

5^˚.

Геометрический смысл определенного интеграла.

L C My=f(x)

f(α₂) D

K B₁ A N

x₀=a x₁, α₁,x₂ x₄=b

Из рис. 1 ≈ площадь криволинейной трапеции АВСD, причем чем “меньше” разбиение отрезка [a,b] тем точнее вычисляется эта площадь.

Если же мы рассмотрим интегральную сумму , то она примерно равна площади фигурыKLMN. И чем мельче разбиение отрезка [a,b] (∆x→0) тем точнее вычислена эта площадь.

Т.е. в пределе lim =S_KLMN

∆x→0

Т.е. определенный интеграл равен площади криволинейной трапеции KLMN.

Примеры.

а) ==

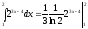б)

в) =

=
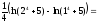