
- •Лекции по алгебре и математическому анализу для студентов заочного (ускоренного) обучения и вечернего (ускоренного) обучения.
- •Ι. Матрицы.
- •Свойства умножения.
- •Ιι. Определители.
- •Определители порядка 2 и 3.
- •Метод Гаусса приведения определителя к треугольному виду (посредством элементарных преобразований).
- •Ιιι Обратная матрица.
- •Явная формула обратной матрицы.
- •Нахождение обратной матрицы по методу Гаусса.
- •Ιv Системы линейных уравнений.
- •Метод Гаусса решения систем линейных уравнений - метод последовательного исключения неизвестных.
- •V Векторы в n-мерном пространстве.
- •Базис и ранг системы векторов.
- •Vι Ранг матрицы.
- •Vιι Однородные системы линейных уравнений.
- •Аналитическая геометрия. Ι Уравнение прямой на плоскости.
- •Расстояние от точки до прямой на плоскости.
- •Угол между прямыми на плоскости. Условие параллельности и перпендикулярности двух прямых.
- •Каноническое уравнение прямой в пространстве.
- •Математический анализ. Ι Геометрический смысл производной.
- •Ι Физический смысл производной.
- •Ι Определение производной.
- •Ι Неопределенный интеграл.
- •Правила интегрирования.
- •V Определенный интеграл.
Ι Физический смысл производной.
Пусть точка движется по закону S = S(t) S - пройденный путь, t - время. Необходимо найти скорость точки в момент времени t0.
К
моменту t0
пройденный
путь равен S0
= S(t0)
а
к моменту t0
+
 -путь
S0
+
-путь
S0
+
 =S(t0
+
=S(t0
+ )
)
Тогда
за промежуток времени
 средняя
скорость
средняя
скорость
 будет
будет

 .Чем
меньше
.Чем
меньше
 ,
тем
лучше средняя скорость характеризует
движение точки в момент t0.
Поэтому
под скоростью в момент t0
естественно
понимать предел средней скорости за
промежуток от t0
до
t0
+
,
тем
лучше средняя скорость характеризует
движение точки в момент t0.
Поэтому
под скоростью в момент t0
естественно
понимать предел средней скорости за
промежуток от t0
до
t0
+ когда
когда

 ,
т.е.
,
т.е.
 =
lim
=
lim
 = lim
= lim =
=
∆t ∆t
∆t
( -значение
производной от функции S(t)
в
точке
t0).
-значение
производной от функции S(t)
в
точке
t0).
Ι Определение производной.
Пусть
задана функция у = f(x)
на
[a,b]
(т.е.
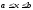 ).
Возьмем
точку
x0
).
Возьмем
точку
x0
 [a,b],
придадим
значению
x0
“очень
малое” (∆х
[a,b],
придадим
значению
x0
“очень
малое” (∆х )
приращение
∆х,
тогда
функция у = f(x)
получит
приращение ∆
)
приращение
∆х,
тогда
функция у = f(x)
получит
приращение ∆ -
- .
.
Определение 1. Производной функции у = f(x) в точке x0 называется предел отношения приращения функции к приращению независимой переменой при стремлении приращения независимой переменно к нулю (если этот предел существует и конечен).
 =
=
∆х ∆х
∆х
Обозначения
производной y’,
 ,
,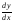 ,
,
Таким образом:
Геометрический
смысл производной: угловой коэффициент
касательной, проведенной к кривой в
точке М0
(x0,y0,),
равен
значению
 производной
в точке x0.
производной
в точке x0.
Физический
смысл производной: значение производной
 в
точке t0
есть
мгновенная скорость материальной точки
в момент времени t0.
в
точке t0
есть
мгновенная скорость материальной точки
в момент времени t0.
Таблица производных.
|
(un)’ = nun-1u’ (cosu)’= -sinu u’
(tgu)’
=
(ctgu)’=
-
(arcsinu)’
=
(arccosu)’=
(arctgu)’=
(arcctgu)’=
-
(au)’
= aulna
(eu)’
= eu
(logau)’
=
(lnu)’
=
|
Правая часть таблицы - это производная сложной функции (получается из теоремы о производной сложной функции).
Правила дифференцирования.
(cu)’ = cu’
(u )’
= u’
)’
= u’ ’
’
(uv)’ = u’v +uv’
 .
.
Пример 1. Вычислить производную.
a)
y = tg2 ,
y’ =
,
y’ =
б)
y = ln(x2
+ 1), y’ =

в)
y = sin5 +
arctgex
, y’ = (sin5
+
arctgex
, y’ = (sin5 )’
+ (arctgex)’
= 5cos5
)’
+ (arctgex)’
= 5cos5 +
+
г)
(cos3 )’
= 3cos2
)’
= 3cos2 (cos
(cos )’
= 3cos2
)’
= 3cos2 (-sin
(-sin )
)
д)
 =
=
=
Ι Неопределенный интеграл.
Определение
1.
Функция
F(x)
называется
первообразной функцией для функции
f(x)
на
[a,b],
если
в каждой точке x [a,b]
F’(x)
=
[a,b]
F’(x)
=
 (x)
(x)
Например
F(x)
= -cos является
первообразной для функции f(x)
= sin
является
первообразной для функции f(x)
= sin ,
функция
x3
является
первообразной для функции
3x2
, т.к.
(x3)’
= 3x2
,
функция
x3
является
первообразной для функции
3x2
, т.к.
(x3)’
= 3x2
Теорема 1. Если функция f(x) определена на [a,b], имеет на этом отрезке производную f’(x), и f’(x) = 0 на [a,b], то f(x) = const.
Теорема 2. Если F1(x) и F2(x) - первообразные для функции f(x) на некотором отрезке [a,b], то существует такое число с, что F2(x) = F1(x) + c
Доказательство.
Так как (F2(x)
- F1(x))’
= F2’(x)
- F1’(x)
= f(x)
- f(x)
= 0, то
F2(x)
- F1(x)
= с
= const.
 F2(x)
= F1(x)
+ c
F2(x)
= F1(x)
+ c
Из данной теоремы следует, что если F(x) первообразная для f(x), то выражение
F(x) + c, где с - произвольное число, задает все первообразные для f(x).
Определение
2.
Совокупность
всех первообразных для функции f(x)
на
промежутке [a,b]
называется
неопределенным интегралом от функции
f(x)
и
обозначается ,
где
,
где
 -
знак
интеграла, f(x)
- подынтегральная
функция,
f(x)dx
- подынтегральное
выражение.
Таким образом
-
знак
интеграла, f(x)
- подынтегральная
функция,
f(x)dx
- подынтегральное
выражение.
Таким образом =
F(x)
+ c,
где
F(x)
- некоторая
первообразная для f(x),
с
- произвольная постоянная
=
F(x)
+ c,
где
F(x)
- некоторая
первообразная для f(x),
с
- произвольная постоянная
Таблица интегралов.
 ,
n
,
n -1
-1
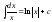 ,
x
,
x 0
0










