Panin_M_P_Modelirovanie_perenosa_izluchenia

4. Обобщим предыдущий случай: источник не только неправильный по форме, но и неравномерный. Потребуем, однако, чтобы функция источника была ограниченной: Qr (r) ≤ Qm . Тогда в целом применим подход варианта 3.

Исключающая функция h(r ) = Qr (rr)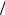g(r ) останется внутри параллелепипеда ограниченной сверху, причем мажоранта hm = Qm V0 . Тогда отнормированная исключающая функция будет

результата, в противном случае отбрасывается, и возвращаемся к п. «а».

Эффективность полученного алгоритма ε = 1/QmV0.

Набор рассмотренных вариантов позволяет разыгрывать источники для широкого круга практических задач.

В дополнение к ним, для источников правильных геометрических форм (цилиндр, шар, конус и т.п.) путем выбора подходящей системы координат могут быть составлены высокоэффективные алгоритмы прямого розыгрыша, не использующие метода исключения. Рассмотрим в качестве примера алгоритм получения случайной точки рождения частицы в цилиндрическом равномерном источнике, ось которого совпадает с осью Z. Функция такого источника выражается через его радиус R и координаты крышек z1 и z2 следующим образом:

Нормированная на единицу функция источника играет роль плотности вероятности рождения частицы, которую выразим через соответствующую функцию распределения FV

Qr (rr) = dFdVV .

101

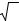
Точка r в цилиндрических координатах задается координатой z, удалением от оси ρ и азимутальным углом ψ относительно плоскости ZOX, а элемент объема вокруг нее равен dV = dzρdρdψ . Разделим переменные в функции распределения

FV = Fz Fρ Fψ. Для пространственной функции источника получим:

переменных z, ρ и ψ. Явный вид этих плотностей таков:

Отсюда методом обратной функции для розыгрыша случайных координат будем иметь:

Случайная точка rξ получена.

Если источник представляет собой набор из нескольких простых по форме тел, может быть полезен метод суперпозиции.

§8.2. Угловое распределение излучения

Определяется функцией QΩ (Ω) . Разыграв ее, получаем случайное направление вылета рожденной частицы Ωξ . Рассмотрим два типовых варианта.

1. Мононаправленный источник («тонкий луч» вдоль r

направления Ω0 )

r

QΩ (Ω) =δ (Ω − Ω0 )

для розыгрыша прост: Ωξ = Ω0 .

2. Изотропный источник: QΩ (Ω) =1/ 4π .

Поскольку функция QΩ (Ω) нормирована на единицу, она представляет собой плотность вероятности вылета частицы в

102

направлении Ω или, используя соответствующую функцию распределения FΩ

QΩ (Ωr) = dFdΩΩ .

Вектор направления Ω задается в сферических координатах независимыми углами θ и ψ, а дифференциал телесного угла вокруг него dΩ = sinθ dθ dψ = dμdψ (см. рис. 3.3). Разделим переменные в функции распределения FΩ = Fμ Fψ. Для угловой функции источника получим:

ψ.

Поскольку μ изменяется от –1 до 1, а ψ – от 0 до 2π, а также из формулы (8.4), следует что

тригонометрические функции cosψξ и sinψξ. Вычислять их по значению ψξ – довольно длительная операция, поэтому разумно воспользоваться алгоритмом, предложенным Дж. Фон Нейманом для розыгрыша непосредственно косинуса и синуса угла, равномерно распределенного на сегменте [0, 2π]:

а) выбираем два случайных числа ξ1, ξ2; б) если ξ12 + ξ22 > 1, отбрасываем их и возвращаемся на шаг

«а»;

в) вычисляем

103

где функция sign(x) равна 1 при x ≥ 0 и –1 при x < 0.

После того как получены случайные значения μξ, cosψξ и

Кроме описанного выше метода моделирования случайного направления вылета частицы из изотропного источника, может быть использован следующий алгоритм:

а) выбираем три случайных значения γ1 = 2ξ1 - 1, γ2 = 2ξ2 - 1,

γ3 = 2ξ3 - 1;

б) если γ12 + γ22 + γ32 > 1, отбрасываем их и возвращаемся на шаг «а»;

в) вычисляем d = γ12 +γ22 +γ32 ;

г) вычисляем Ωξ x =γ1 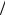d ; Ωξ y =γ2 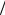d ; Ωξ z =γ3 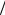d .

Как видим, реализован метод исключения. Эффективность розыгрыша равна π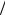6 .

§8.3. Энергетическое распределение излучения

Определяется спектральной функцией QE (E) . После ее розыгрыша получим случайную энергию рожденной частицы Eξ .

Рассмотрим два часто встречающихся на практике варианта задания спектра.

1. Радионуклид, обладающий N линиями излучения.

Для получения нормированной спектральной функции обратимся к справочнику и установим набор энергий Ei и выходов

(% на распад) ηi каждой из линий: {Ei ,ηi },i =1,..., N .

Относительные доли излучения каждой линии вычисляются просто:

N

Pi =ηi ∑ηj . j=1

С их помощью нормированная спектральная функция

N

QE (E) = ∑Pi δ (E − Ei )

i=1

104

легко разыгрывается методом суперпозиции, поскольку энергия представляет собой дискретную случайную величину. Находим номер линии:

и случайное значение энергии Eξ = Ekξ .

2. Спектр задан в виде результата эксперимента.

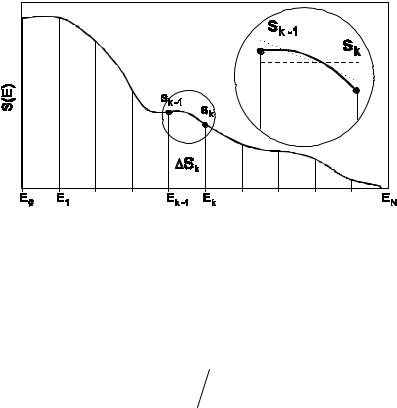
Пусть требуется разыграть энергию по спектру, полученному в результате измерения (рис.8.1). Во-первых, следует убедиться, что представленный спектр отражает именно количество частиц, испущенных в единицу энергетического интервала, а не испущенную источником энергию, или поглощенную энергию в кристалле спектрометра, или какую-то другую величину.

Рис.8.1. Обработка экспериментального спектра

Если с физическим смыслом экспериментальных данных все

впорядке, необходимо отнормировать полученный спектр. Для этого весь энергетический диапазон разбивается на N интервалов, так что k-й интервал имеет границы [Ek-1, Ek], а значения функции

вних – sk-1 и sk. Подсчитаем площадь под функцией на k-м

интервале и обозначим ее Sk. Вычислим вероятность того, что испускаемая частица принадлежит k-му интервалу:

N

Pk = Sk ∑ Si .

i=1

105

После этого случайный номер интервала kξ находим из формулы (8.10). В зависимости от желаемой точности представления спектральную плотность вероятности внутри интервала можно приблизить:

а) константой (штриховая линия на рис.8.1), б) линейной зависимостью (пунктирная линия на рис.8.1).

Оба этих приближения обеспечивают простые схемы розыгрыша энергии методом обратной функции:

а) Eξ = Ek−1 +ξ2 (Ek − Ek−1 ),

Приведенный алгоритм фактически реализует метод суперпозиции, поэтому обратим внимание, что случайные числа

при выборе интервала kξ (8.10) и самой энергии Eξ должны быть разными.

Контрольные вопросы

Перечислите основные этапы моделирования источника.

Напишите плотность вероятности точки рождения частицы в равномерном объемном источнике.

Как может быть разыграна точка рождения частицы в равномерном источнике неправильной геометрической формы?

Какова последовательность розыгрыша энергии частицы, вылетающей из радионуклидного источника?

Как можно разыграть энергию частицы, если спектр источника задан графически?

Напишите алгоритм розыгрыша направления вылета частицы из изотропного источника.

106

Глава 9. Моделирование транспортного ядра

Когда ж, и где, в какой пустыне…? А.С. Пушкин

§9.1. Общая схема розыгрыша длины свободного пробега в среде

Транспортное ядро имеет смысл вероятности для частицы,

вылетающей из точки r′в направлении Ω с энергией E, испытать очередное столкновение в единице объема вокруг точки r . Оно было введено ранее формулой (4.16) в следующем виде:

задается выражением (4.1).

Представим конечную точку полета частицы r через точку вылета rr′в сферических координатах: rr = r ′ + t ω . В этой записи t = rr − rr′ , т.е. расстояние между точками, а ω есть единичный вектор направления:ωr = (r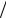r − rr′)rr − rr′ .

Розыгрыш случайной точки следующего столкновения rξ эквивалентен розыгрышу случайного направления ωξ т.е. луча, на

котором будет находиться эта точка, и случайного пробега tξ, который преодолеет частица вдоль этого луча.

Исходя из физического смысла транспортного ядра, представим ядро в виде плотности вероятности:

Для совместной плотности вероятности получим следующее явное

выражение:

pT (t,ωr) = Σ(rr, E) e−τ (rr′→rr,E) δ (Ω −ωr) .

Ввиду того, что в плотности присутствует δ-функция, розыгрыш случайного вектора ω очевиден: ωrξ = Ω. Тогда плотность вероятности для пробега:

107

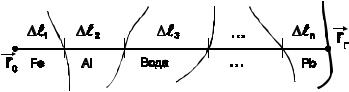
pt (t) = Σ(rr′ + t Ω, E) e−τ(rr′→rr′+t Ωr,E) .

Если от линейного пробега t перейти к оптическому τ, то для него, используя выражение (4.1), можно найти плотность вероятности

Случайный оптический пробег, распределенный с плотностью (9.1) на полуоси [0,∞), легко разыгрывается методом обратных функций:

разыгранному оптическому пробегу τξ зависит от свойств среды, в которой происходит перенос излучения.

Однородная среда предполагает, что сечение взаимодействия во всех точках среды одинаково, т.е. Σ(r , E) = Σ(E) . В этом

простом случае

Если среда ограничена, и полученный пробег превосходит расстояние до границы, частица считается вылетевшей, и ее история заканчивается.

Кусочно-однородная среда является более общим случаем, при котором вся среда состоит из областей, в каждой из которых сечение неизменно. Отрезок между двумя произвольными точками rr1 и rr2 разбивается на набор интервалов { li}, i =1,..., n с

постоянными значениями сечений (рис.9.1).

Рис.9.1. Схема пробега в кусочно-однородной среде

В этом случае линейный пробег tξ находится последовательным сравнением разыгранного оптического пробега

108

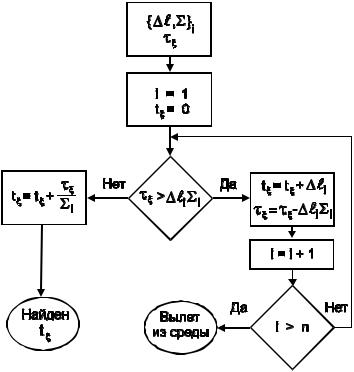
соптической толщиной каждого интервала. Один из возможных

алгоритмов нахождения tξ приведен на рис.9.2.

Практические задачи, требующие расчета переноса в средах

сплавно меняющимися свойствами среды, встречаются редко. Примером такой задачи является расчет переноса излучения от источника, расположенного в верхних слоях атмосферы. На больших высотах плотность воздуха настолько мала, что на расстояниях, сравнимых с пробегом излучения, она может заметно изменяться. Закон изменения плотности с высотой хорошо известен и на ограниченных интервалах может быть описан аналитической зависимостью. Однако общим подходом в таких расчетах является разбиение атмосферы на слои с постоянной плотностью внутри слоя и сведением задачи к случаю кусочнооднородной среды.

Рис.9.2. Блок-схема алгоритма розыгрыша пробега в кусочнооднородной среде

109

§9.2. Универсальные геометрические модули

Геометрический модуль программы, реализующей метод Монте-Карло, решает следующие задачи:

1.Описание геометрии, в которой происходит перенос излучения.

Модуль должен предоставить программе исчерпывающую

информацию о том, какие вещества входят в область переноса и какова геометрическая конфигурация подобластей, которые заполнены этими веществами.

2.Определение вещества в любой точке и оптического вектора между двумя произвольными точками области переноса.

В данной главе будем считать, что пространство, в котором

происходит перенос излучения, представляет собой кусочнооднородную по характеристикам вещества область. Тогда отрезок прямой, соединяющий две произвольные точки r1 и r2 , может

быть представлен как набор из n интервалов li между границами однородных подобластей (рис. 9.1). В каждой подобласти неизменны номер mi и плотность ρi вещества. Это набор будем

Существуют два альтернативных подхода к построению геометрических модулей.

1.Специализированные геометрические модули предусматривают программирование отдельного модуля для каждой конкретной расчетной задачи наряду с программированием собственно алгоритма решения задачи. Этот подход позволяет написать более экономные по затрачиваемым ресурсам и быстрые модули. Полученные модули, однако, совершенно негибкие, и в случае изменения геометрии их приходится перепрограммировать заново. Такой подход оправдан, если геометрия простая (например, двухкомпонентная бесконечная область, разделенная плоской внутренней границей: воздух-земля, воздух-вода и т.п.), а создаваемая программа предназначена для решения одной конкретной задачи.

2.Универсальные геометрические модули, в отличие от специальных, получаются более медленными и требовательными к используемым ресурсам. Они, однако, обладают неоспоримым

110