Примеры расчетов

1.Рассчитать pH 0,4 % -го раствора едкого натра.

Решение. Переведем процентную концентрацию в молярную: в 1 литре данного раствора содержится 4 г едкого натра (плотность раствора считаем равной единице), т.е. 0,1 моль. Каждому молю гидроксида натрия (сильного основания) соответствует один моль гидроксид-ионов, следовательно, концентрация их в растворе также будет равна 0,1 М. Применим формулу (11): pOH = - lg 0,1 = 1; pH = 14 - pOH = 14 - 1 = 13.

2.Рассчитать pH 0,01 М раствора цианида натрия.

Решение. Цианид натрия - основание, так как катионы натрия протолизу не подвергаются, а цианид-ионы связывают протоны, образуя слабую синильную кислоту. По справочнику находим pK_aдля перехода HCN / CN^–= 9,21. Рассчитываем значение pK_bцианида: = 14 - 9,21 = 4,79. Для данного раствора pC = - lg0,01 = 2,0. Выполняется условие pK_b > pC +2, т.е. цианид можно считать очень слабым основанием. Расчет производим по приближенной формуле (13):

pOH = = 0,5 (4,79 + 2,0)1,7 ; pH = 14 - pOH = 12,3.

3.Рассчитать pH 0,001 М раствора муравьиной кислоты.

Решение. По справочнику находим pK_a= 3,8, кислота слабая,

pC = - lg 0,001 = 3, условие pK_a > pC +2 не выполняется, считать по приближенной формуле нельзя.

Составляем уравнение:

HA = H + A (заряды опускаем)

K_a==.

Отсюда

[H] = -K_a/2 += -10^-3,8/2 +3,3·10^-4;

pH = -lg 3,3.10^-4= 3,48 (3,5. При вычислении рН по упрощенной формуле мы получили бы значение pH = 3,4.

4.Вычислить pH 0,01 % -го раствора гидрокарбоната натрия.

Решение.Гидрокарбонат-ион может как отдать протон (превращаясь в карбонат), так и принять его от молекулы воды, превращаясь в угольную кислоту. Поэтому гидрокарбонат- ион следует считать амфотерной частицей, а в растворе одновременно находятся все три формы угольной кислоты. Для угольной кислоты в справочнике находим: pK_a1 = 6,35 (переход Н₂СО₃/ HCO₃₎, pK_a2= 10,32 (переход НСО₃/ CO₃). Общая концентрация карбонатов в данном случае значения не имеет. Расчет производится по формуле (14):

pH = 0,5 (6,35 + 10,32) = 8,34.

5.Рассчитать pH 0,01 М раствора серной кислоты.

Решение.Запишем уравнение диссоциации серной кислоты: H₂SO₄ = 2H⁺+ SO₄^2–. Серная кислота - сильная, в водном растворе она подвергается 100 %-му протолизу по первой ступени, а степень протолиза по второй ступени также близка к 100%, следовательно, в растворе концентрация ионов водорода равна молярной концентрации кислоты, умноженной на 2, т.е. 0,02 и pH = - lg 0,02 = 1,7. Более точный расчет, учитывающий неполный протолиз по второй ступени, дает величину рН 1,8.

6.Рассчитать pH 0,1 М HCl в присутствии 0,01 моль/л сульфата алюминия.

Решение. HCl - сильная кислота, в растворе полностью подвергается протолизу (диссоциирует), следовательно, [H⁺] = C_HCl= 0,1. Но в растворе присутствует значительное количество сильного многозарядного электролита - Al₂(SO₄)₃, и активность ионов водорода значительно отличается от концентрации. Рассчитаем ионную силу раствора: I [Al₂(SO₄)₃] = 0,5 (0,02·3²+ 0,03·2²) = 0,15.

Следует учесть ионную силу, создаваемую самой хлористоводородной кислотой. Для нее I = С_HCl = 0,1. Общая ионная сила раствора, таким образом, равна 0,25. При такой ионной силе коэффициент активности однозарядных ионов водорода лучше взять по справочнику [8, с.87]: f_H = 0,80. Поэтому активность Н^+–ионов равна 0,080, а pH1,1.

7.Рассчитать pH раствoра, в 150 мл которого имеется 15 г KCN и 10 г HCN.

Решение. Раствор содержит одновременно слабую кислоту и ее сопряженное основание - цианид-ионы. С учетом молярных масс компонентов вычисляем молярные концентрации компонентов буфера:

[HCN] = 2,47 (моль/л); [KCN] = 1,54 (моль/л).

Применяя формулу (15) для вычисления pH буферных растворов, получим pH = pK_a+ lg 1,54 / 2,47 = 9,21 - 0,21 = 9,00.

8.Требуется приготовить 2 л 0,25 М буферного раствора с pH 5,0. Предложить методику приготовления такого буфера.

Решение. Выбираем сопряженную пару «кислота - основание» (по Бренстеду) так, чтобы pH буфера отличался бы от pK_aпары менее чем на единицу. По таблице констант ионизации находим кислотно-основную пару, удовлетворяющую этому условию: для перехода HAc / Ac^–значение pK_a= 4,74, причем компоненты буфера (уксусная кислота и ее соли) достаточны инертны, растворимы и доступны. Расчет проводим по формуле (15), но заменяя в ней отношение концентраций отношением числа молей обеих форм:

pH = pK_a + lg _Ac /_HAc.

Так как в 2 л 0,25 М буфера содержится 0,50 моля суммы (HAc + Ac^-):

_Ac + _HAc = 0,50 ; pH = 5 = 4,74 + lg (0,5 - _Hac) / _HAc.

Отсюда после простых преобразований получается _HAc= 0,177;

_Ac-= 0,5 - 0,177 = 0,323.

Переведем число молей HAc и Ac^-в массы:

m_HAc = _Hac. M_HAc = 0,177 · 60,0 = 10,6 (г);

m_NaAc = _Ac. M_NaAc= 0,323 · 82,0 = 26,5 (г).

Для приготовления буфера необходимо взять 10,6 г ледяной уксусной кислоты и 26,5 г ацетата натрия, растворить в воде и довести объем раствора до 2 л.

9.Как изменится pH одномолярного аммиачного буфера с pH = 9, если к 150 мл его прилить 20 мл 5%- й соляной кислоты?

Решение.При протекании в среде буфера реакций, сопровождающихся выделением или связыванием протонов, величину рН* следует рассчитывать по формуле (15а). Перед основным расчетом вычислим первоначальное число молей компонентов буфера (до введения HCl), а также число молей НСl. Буфер одномолярный, т.е.

[NH₃] + [NH₄] = 1;

Взято 150 мл буферного раствора: [NH₃] +[NH₄] = 0,15.

Из условия задачи известно первоначальное значение pH:

9 = 9,26 + lg [NH₃] / [NH₄] = 9,26 + lg (0,15 - [NH₄]) / [NH₄]).

Решая последнее уравнение, получим

(0,15 - [NH₄])/[NH₄] = 0,55;

[NH₄] = 0,097;[NH₃] = 0,15 - 0,097 = 0,053.

В 20 мл 5%-й HCl содержится 20·0,05 = 1 г хлористого водорода, т.е. 1/36,5=0,027 моль. Плотность раствора HCl приняли равной единице. Подставляя найденные величины в формулу (15а), получаем:

рН* = 9,26 + lg= 8,28,

что и требовалось определить по условию.

Можно было построить следующую цепочку рассуждений (начинающим такой вариант решения понятнее):

При приливании кислоты к буферному раствору идет реакция:

H⁺+ NH₃= NH₄⁺,

т.е. расходуется 0,027 моль NH₃и образуется 0,027 моль NH₄⁺. После реакции в растворе окажется 0,053 - 0,027 = 0,026 моль NH₃. Ионов аммония окажется 0,097 + 0,027, т.е. 0,124 моль. Величину pH полученного раствора рассчитываем по обычной формуле:

pH = 9,26 + lg 0,026/0,124 = 8,58.

Естественно, под действием добавленной соляной кислоты произошло снижение рН буферного раствора, но сдвиг рН относительно невелик - с 9 до 8,6.

10.Составить ионную диаграмму, описывающую состояние пирофосфорной кислоты в водном растворе.

Решение. Поскольку кислота имеет формулу H₄P₂O₇и может находиться в водном растворе в пяти различных формах (молекулы Н₄R и анионы H₃R; H₂R; HR; R, отличающиеся друг от друга не только протонированностью, но и зарядом), необходимо построить пять кривых, изображающих графическую зависимости мольной доли соответствующей формы от рН. Таким образом, диаграмма строится в координатах% = f (pH). При pH = 0 выход молекулярной формы близок к 100%, а по мере повышения pH падает из-за перехода молекул в анионы H₃R^-. Содержание этих ионов постепенно возрастает с ростом рН, а затем снижается, по мере перехода их в ионы H₂R, и т.д., вплоть до сильно щелочной среды, где доминируют анионы R^4-. Для построения кривых необходимо найти в справочниках кислотные константы, соответствующие переходам между формами разной протонированности, Их показатели равны: 0,91; 2,10; 6,70;: 9,32. Из формулы расчета рН буферного раствора следует, что величина pH равна pK_a.при [Кисл.] = [Осн], что соответствует пересечению кривых на ионной диаграмме. Доля каждой из сопряженных форм при этом рН составляет около 50% (если пренебречь наличием других форм кислоты). Очевидно, молекулы Н₄R доминируют при рН < 0,91. Анионы H₃R^-доминируют при рН от 0,91 до 2,10, причем максимальный выход их, приближающийся к 100%, будет на середине интервала (при рН 1,5) и т.д. Таким способом можно получить ионную диаграмму в целом, хотя нельзя достичь высокой точности.

С помощью компьютера можно построить диаграмму гораздо точнее. Программа PROTOLIZ рассчитывает -функции при разных рН. Результат расчета показан на рис.1.

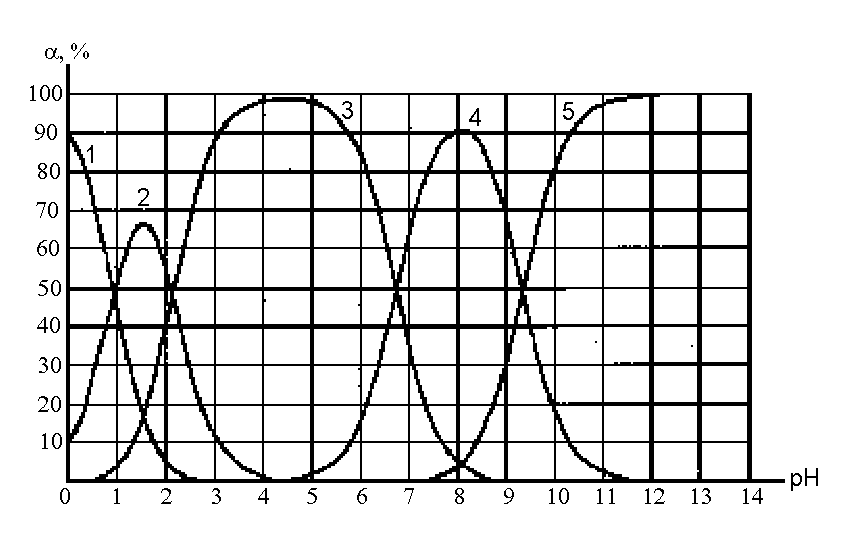
Рис.1. Ионная диаграмма, показывающая состояние пирофосфорной кислоты в водном растворе 1– H₄R;2– H₃R^-;3– H₂R^2-;4- HR^3-;5– R^4-

11.В каких формах при pH = 10 находится сероводород в водном растворе? Рассчитать мольные доли каждой из форм. При каком рН достигается максимальный выход гидросульфид-анионов?

Решение. Сероводородная кислота - двухосновная, в растворе она всегда существует в трех формах: H₂S, HS^-и S^2-. Значения показателей кислотных констант (округленно): pK_a1= 7,0; pK_a2= 12,6. Следовательно, в растворах с рН от 7,0 до 12,6 (в том числе и при рН 10) доминирует форма HS^-. Доли всех форм рассчитаем по формулам (16а):

_Н2S =0,001;

_HS =0,996;

_S =0,003.

Наивысший выход гидросульфидов в середине их зоны доминирования, т.е. при рН = (7,0 + 12,6) / 2 = 9, 8.