8.3. Корреляционный и регрессионный анализ

Для оценки степени связи двух характеристик в корреляционном анализе используется коэффициент корреляции. Оценка коэффициента корреляции по наблюдениям (x_i,y_i),i=1:n рассчитывается по формуле:

где ,.

Значимость оценки определяется с помощью критерия Стьюдента:

если то оценка значима, и не значима в противном случае.

Величина t выбирается из таблицы распределения Стьюдента [ 6 ] и отвечает уровню значимости . (Для =0.05, n=100, t2.0).

Для оценки характера связи в регрессионном анализе используется понятие функции регрессии. Оценка функции регрессии в нормальном случае производится по n наблюдениям (x_i, y_i),i=1:n по формул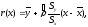е где

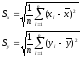
Доверительная область для линии регрессии r(x) определяется как

где

К определяется по уровню значимости (Для =0.05, n=100, К2.0)

В многомерном случае степень связи случайных величин х₁, х₂, …,х_р ,Y определяется с помощью множественного коэффициента корреляции R (0R1).

Его оценка по n наблюдениям (y_i,x_1i,…,x_pi), i=1:n определяется как

где - оценка функции множественной регрессии Y по x₁,x₂,…,x_p

Оценка множественной регрессии в виде линейной функции r(x)=a+b₁x₁+…+b_px_p находится методом наименьших квадратов:

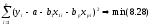
Значимость оценок коэффициентов определяется из условий:

• имеет распределение Стьюдента St_n-p-1;

• имеют распределение Стьюдента St_n-p-1;

• имеет распределение Х²_n-p-1, где

.

Оценка коэффициента является значимой, если значение соответствующей статистики превосходит табличное значение, отвечающее заданному уровню значимости.

8.4. Робастные методы и процедуры

Многие «наилучшие» оценки в статистике (например, наиболее распространенная на практике оценка среднего значения случайной величины ) обладают тем дефектом, что они являются наилучшими лишь в случае, если выборка наблюдений получена из нормально распределённой совокупности данных и быстро теряют свои оптимальные свойства по мере отклонения распределения от нормального, т.е. являются неустойчивыми к отклонениям от нормального распределения. В качестве характеристики устойчивости оценки можно предложить понятие робастности.

Определение робастности оценки. Пусть случайная величина Х имеет плотность распределения вероятностей , где вид функции f известен, а - неизвестный параметр (может быть величиной векторной). Оценка параметрапроизводится поn наблюдениям х₁,х₂,…,х_n. В классической статистике качество оценки определяется её дисперсией D_f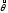, вычисленной в предположении, что выборка получена из генеральной совокупности с плотностью распределения вероятностей .

Определим понятие -окрестности распределения f:

где 0<<1, а h(x) – произвольная плотность распределения вероятностей.

Назовём оценку робастной, если для неё имеет место. То есть робастная оценка – это такая оценка, которая в наихудшем случае (когда достигается) имеет наименьшую дисперсию. Нахождение робастной оценки отвечает решению, как говорят в математике, минимаксной задачи. Минимаксное значение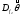есть гарантированный верхний порог дисперсии оценки для любого распределения f из -окрестности.

Минимаксная стратегия широко распространена в таком разделе теории операций как теория игр. В определённом смысле робастная процедура – это «игра» исследователя с природой.

Робастная оценка среднего значения. Если параметр играет роль центра распределения (среднего значения), то f(x,)=f(x-). Робастная оценка параметра в этом случае находится по n наблюдениям х₁,х₂,…,х_n решением следующей задачи:

Если f(x,) – плотность вероятностей нормального распределения, то

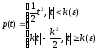, (8.29)

Робастная оценка в этом случае представляет собой некий гибрид оценки средней арифметической () и выборочной медианы (med{x_i}). Она совмещает в себе эффективность первой оценки и устойчивость второй. Их соотношение определяется величиной степени засорения (0<<1) через величину к=к(). Если 0 (к), то оценка близка к среднему арифметическому. Если 1 (к0) , то оценка близка к выборочной медиане.

Робастная оценка имеет вид:

где - вариационный ряд выборочных значений; m=[n], =(k())=(). Значения =() можно найти в таблице 2 [ 6 ].

Таблица 2.

Значения уровня урезания =()

	0	0.001	0.005	0.01	0.05	0.10	0. 20	0.30	0.40	0.50	0.80	1
	0	0.004	0.015	0.026	0.081	0.127	0.194	0.247	0.291	0.332	0.436	0.5

Робастная регрессия. Уравнение регрессии, получаемое методом наименьших квадратов, имеет существенный дефект, заключающийся в том, что при наличии грубых ошибок в данных оценки его коэффициентов сильно искажаются, т.е. являются неустойчивыми к отклонениям от обычного предположения в регрессионном анализе, что ошибки в модели регрессии y=a+b₁x₁+…+b_px_p+ имеют нормальное распределение.

Коэффициенты робастной регрессии вычисляются решением задачи:

где (t) имеет вид (8.29).