
ДЗ по математике 12 для химиков
.rtf1. Какие из следующих функций являются чётными, какие нечётными, какие не являются ни чётными, ни нечётными?
а)
 ; б)
; б)
 ; в)
; в)
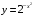 ; г)
; г)
 ;
д)
;
д)
 ; е)
; е)
 ; ж)
; ж)
 ; з)
; з)
 .
.
2. Доказать, что произведение двух чётных функций есть чётная функция, произведение двух нечётных – чётная функция, произведение чётной и нечётной функций – нечётная функция.
3. Построить
график периодической функции с периодом
T=2,
которая на интервале [-1,1)
задана формулой: а)
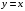 ; б)
; б)

4. Указать область определения, множество значений, интервалы монотонности функций, графики которых приведены на рисунке. Являются ли функции ограниченными снизу, ограниченными сверху, строго ограниченными? Являются ли они непрерывными?

5.
Построить
в одной системе координат графики
функций а) ,
,
 ,
,
 ;
б)
;
б) ,
,
 ,
,
 ;
в)
;
в)
 ,
,
 ,
,
 .
.
6. Начертить графики функций:
(1)
Степенная функция с натуральным
показателем степени

а) для n=3, 5; б) для n=2, 4;
(2)
Степенная функция с целым
отрицательным показателем степени

а) для n=3; а) для n= 4;
(3)
Степенная
функция
с показателем
степени
 :
:

а) для n=3, 5; б) для n=2, 4;
(4)
Показательная функция

а) при 0<a<1, б) при a>1;
(4)
Логарифмическая функция

а) при 0<a<1, б) при a>1;
(5) Тригонометрические функции
а)
синус
 ;
б) косинус
;
б) косинус
 ;
в) тангенс
;
в) тангенс
 ;
;
г)
котангенс
 ;
д) секанс
;
д) секанс
 ;
е) косеканс
;
е) косеканс
 .
.
(6) Обратные тригонометрические функции
а)
арксинус
 ;
б) арккосинус
;
б) арккосинус
 ;
;
в)
арктангенс
 ;
г) арккотангенс
;
г) арккотангенс
 .
.
Замечание:
При выполнении этого задания вначале переписать заголовок (выделен жирным шрифтом), а затем построить графики.
Если в каком-то задании указано несколько кривых, следует строить их в одной системе координат. Так, например, результат выполнения задания 6. (1) б) выглядит следующим образом:
7. Познакомьтесь с описанием и изображением таких кривых, как спираль Архимеда, декартов лист, кардиоида, астроида, лемниската Бернулли, строфоида, улитка Паскаля.
Замечание.
Пример описания: Астроида – линия,
которую описывает точка, принадлежащая
окружности при качении этой окружности
(без проскальзывания) по другой неподвижной
окружности, касаясь ее внутренним
образом. Параметрическое уравнение:
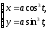 для
для
 .
.
График изображен на рисунке красным.
