
ВЕКТОРЫ И ДЕЙСТВИЯ НАД НИМИ
.docxII. ВЕКТОРЫ И ДЕЙСТВИЯ НАД НИМИ
-
Сложение векторов
-
Умножение вектора на число
-
Базис и размерность
______________________________________________________________________________
II.0 ПОНЯТИЕ ВЕКТОРА
Вектор на прямой ℓ – любой направленный отрезок ∈ ℓ
Вектор на прямой/плоскости/в R3 – любой направленный отрезок,
лежащий на прямой/плоскости/в R3
Векторы, растущие из точки и действия над ними
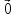 -вектор
– вектор, начало которого спвпадает с
концом.
-вектор
– вектор, начало которого спвпадает с
концом.
Коллинеарные векторы – ненулевые векторы, принадлежащие одной прямой
либо 2м ||
прямым. -вектор
коллинеарен любому вектору. Каждый
вектор коллинеарен сам себе.
Обозначение:
-вектор
коллинеарен любому вектору. Каждый
вектор коллинеарен сам себе.
Обозначение:
 ||
||
Компланарные векторы – векторы, принадлежащие одной плоскости, либо лежащие в параллельных плоскостях.
Равные векторы – а.) Коллинеарны, сонаправлены; б.) Имеют равные длины
Направленность векторов –
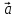 ↑↑
↑↑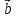 – сонаправлены;
– сонаправлены;
 ↑↓
↑↓ – разнонаправлены
– разнонаправлены
______________________________________________________________________________
II.1 СЛОЖЕНИЕ ВЕКТОРОВ
-
Правило параллелограмма

-
Правило треугольника

-
Правило ломаной
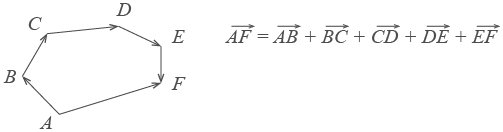
При
сложении векторов ![]() и
и ![]() получаем:
получаем:
![]()
![]()
СВОЙСТВА:
-
Коммутативность

-

-
Ассоциативность
-

-

-
-
Существование нулевого вектора
-
 ;
;
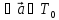
-

-
Существование обратного вектора
-

-

-

-
______________________________________________________________________________
-
II.2 УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
-
При умножении вектора
 на число
на число  получается
вектор
получается
вектор
 ,
длина которого в
,
длина которого в  раз
отличается от длины
раз
отличается от длины  .
. -
 ||
|| ;
;
 ↑↑
↑↑ при
при
 ;
;
 ↑↓
↑↓ при
при

-
 =
=
-
Направление: при
 вектор меняет
направление на
противоположное
вектор меняет
направление на
противоположное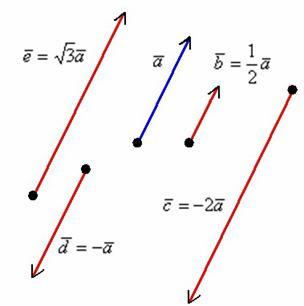
-
Длина: Если
 или
или
 ,
то длина вектора уменьшается.
,
то длина вектора уменьшается.
-
Если
 ,
то
длина вектора увеличивается в
,
то
длина вектора увеличивается в  раз.
раз. -
Все векторы коллинеарны.
-
-
-
-
______________________________________________________________________________
-
II.3 БАЗИС И РАЗМЕРНОСТЬ ЛИНЕЙНОГО (ВЕКТОРНОГО) ПРОСТРАНСТВА
-
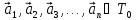
-

-
-
Размерность векторного пространства – число, равное максимальному количеству линейно независимых векторов в этом пространстве.
-
Базис векторного пространства – упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.
-
-
1. Линейная комбинация векторов – выражение
-

-
2. Линейная зависимость
-
 называются
линейнозависимыми,
если
называются
линейнозависимыми,
если
 линейная комбинация этих векторов =
0, при этом хотя бы 1 из коэфф.
линейная комбинация этих векторов =
0, при этом хотя бы 1 из коэфф. комбинации
комбинации
 .
. -
3. Линейная НЕзависимость
-
 называются
линейнозависимыми,
если
называются
линейнозависимыми,
если
 линейной комбинация этих
линейной комбинация этих -
векторов = 0, при этом хотя бы 1 из коэфф.
 комбинации
комбинации
 .
. -
-
Случай №1
-
ДАНО: n=1
-

-
 ;
;

-

-

-
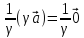
-

-
Случай №2
-
ДАНО: n=2
-

-
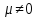
-

-

-
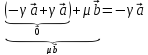
-

-
-

-
-

-

-
-

-
-
 – линейно
зависимы;
– линейно
зависимы;
 ||
||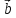
-
-
Случай №3
-
ДАНО: n=3
-

-
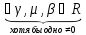
-
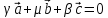 ;
;
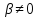
-

-

-
-
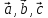 – линейно
зависимы
– линейно
зависимы -
Хотя бы 1 из векторов
 может быть
представлен в виде линейной комбинации
векторов
может быть
представлен в виде линейной комбинации
векторов
 хотя бы одна линейная комбинация
векторов может быть представлена в
виде вектора
хотя бы одна линейная комбинация
векторов может быть представлена в
виде вектора
 .
. -

