
1 курс 2 семестр / Mathematic
.docДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
271 - 280. Найти решения дифференциальных уравнений первого порядка, удовлетворяющие указанным начальным условиям.
271. 3x + xy![]() +
+
![]() y
y![]() =
0, y(1) = 1.
=
0, y(1) = 1.![]()
272. xyy![]() +
x
+
x![]() e
e![]() -
y
-
y![]() = 0, y(1) = 1.
= 0, y(1) = 1.
273. xdx + ydy
= 5x![]() ydy
- 10 xy
ydy
- 10 xy![]() dx
, y(1) = 1.
dx
, y(1) = 1.
274. xy![]() = y - y ln ( y/x ), y(1) = 1.
= y - y ln ( y/x ), y(1) = 1.
-
(xy
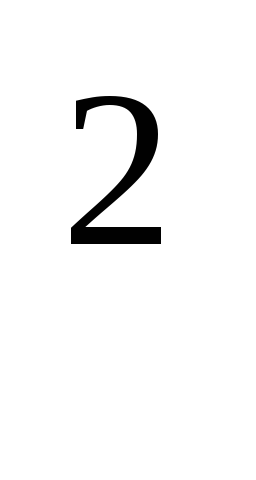 + x) dx +
+ x) dx +
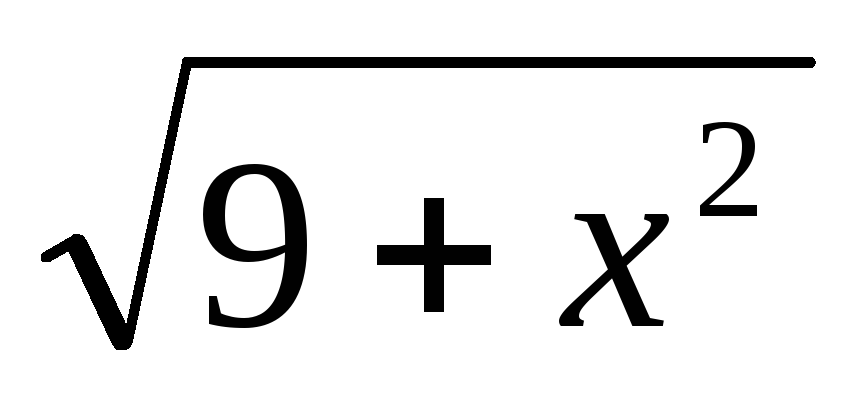 dy
= 0, y(0) = 0.
dy
= 0, y(0) = 0. -
y
 + 2xy = x e
+ 2xy = x e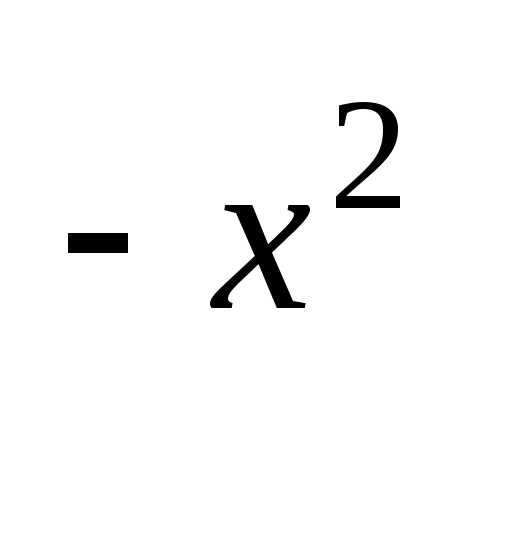 ,
y(0) = 1.
,
y(0) = 1. -
xy
 + y = y
+ y = y ,
y(1) = 2.
,
y(1) = 2. -
xy
 = y - x tg
= y - x tg
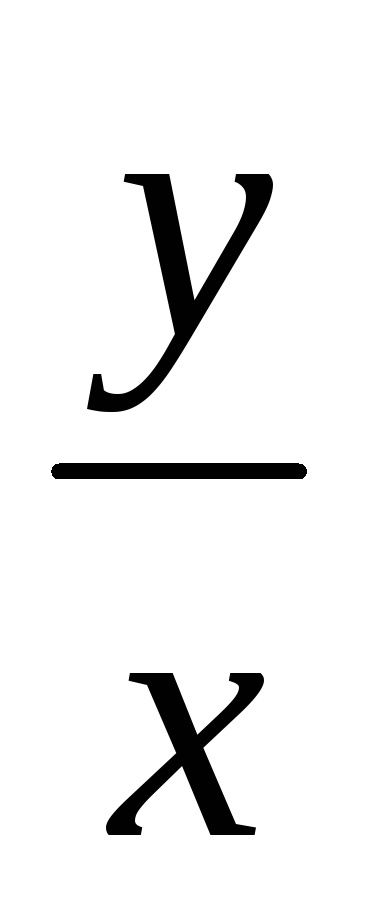 ,
y(1) =
,
y(1) =
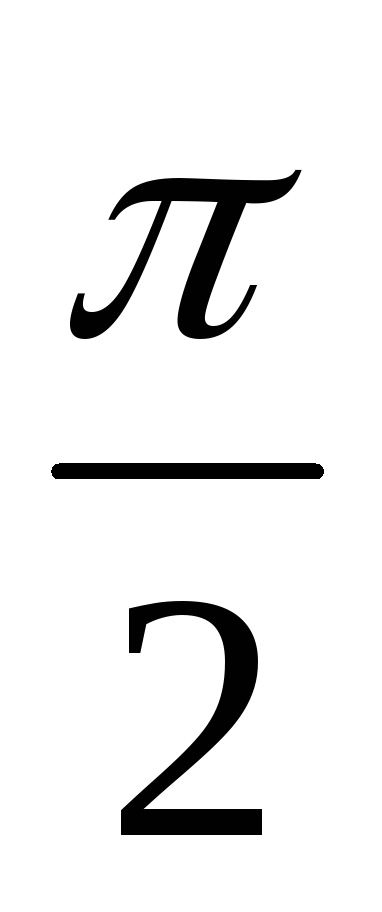 .
. -
(1 + x
 )y
)y - 2xy = (1 + x
- 2xy = (1 + x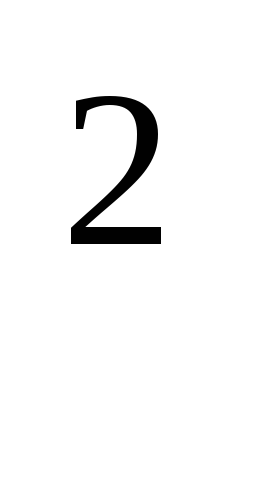 )
) ,
y(0) = 1.
,
y(0) = 1. -
xy
 + y = e
+ y = e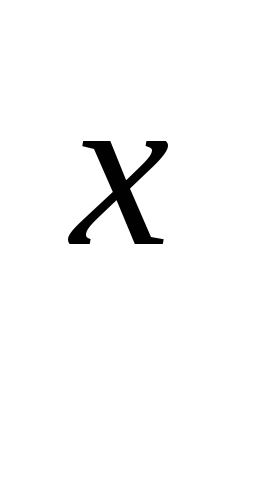 , y(0) = 1.
, y(0) = 1.
281 - 290. Решить дифференциальные уравнения второго порядка: а) найти общее решение; б) найти решение, удовлетворяющее указанным начальным условиям.
-
а) xy
 +
y
+
y = x
= x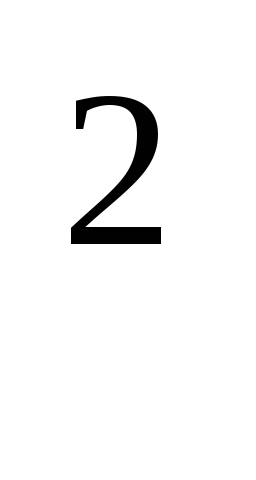 .
.
б) y![]() - 3y
- 3y![]() = e
= e![]() ,
y( 0 ) = -2, y
,
y( 0 ) = -2, y![]() (
0 ) = 1 .
(
0 ) = 1 .
-
а) 2y y
 - (y
- (y )
)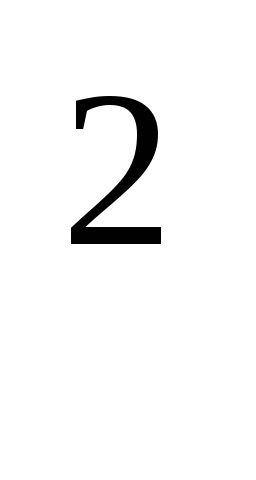 =
0.
=
0.
б) y![]() - 3y
- 3y![]() + 2y = x – 1 , y( 0 ) = 1, y
+ 2y = x – 1 , y( 0 ) = 1, y![]() (
0 ) = 0.
(
0 ) = 0.
-
а) y
 - y
- y ctg
x = sin x.
ctg
x = sin x.
б) y![]() - 6y
- 6y![]() + 9y = 5sin 3x , y( 0 ) = 0, y
+ 9y = 5sin 3x , y( 0 ) = 0, y![]() (
0 ) = -1.
(
0 ) = -1.
-
а) y
 ctg
y - 2(y
ctg
y - 2(y )
)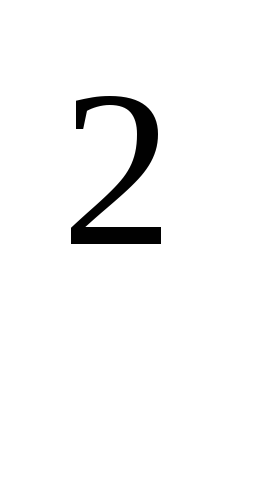 =
0.
=
0.
б) y![]() + 2y
+ 2y![]() + 10y = x
+ 10y = x![]() , y( 0 ) = -1, y
, y( 0 ) = -1, y![]() (
0 ) = 0.
(
0 ) = 0.
-
а) y
 ctg
x - y
ctg
x - y +
2 = 0.
+
2 = 0.
б) y![]() + 4y = 2e
+ 4y = 2e![]() , y( 0 ) = 3, y
, y( 0 ) = 3, y![]() (
0 ) = 0.
(
0 ) = 0.
-
а) 2y
 y
y y
= 1 +( y
y
= 1 +( y )
)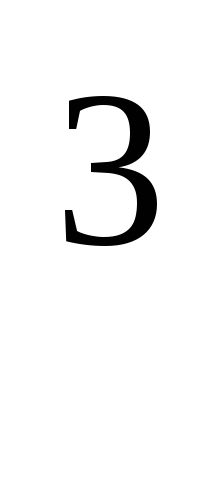 .
.
б) y![]() - 9y = -2cos x , y( 0 ) = 1, y
- 9y = -2cos x , y( 0 ) = 1, y![]() (
0 ) = -1.
(
0 ) = -1.
-
а) x y
 - y
- y =
y
=
y ln
ln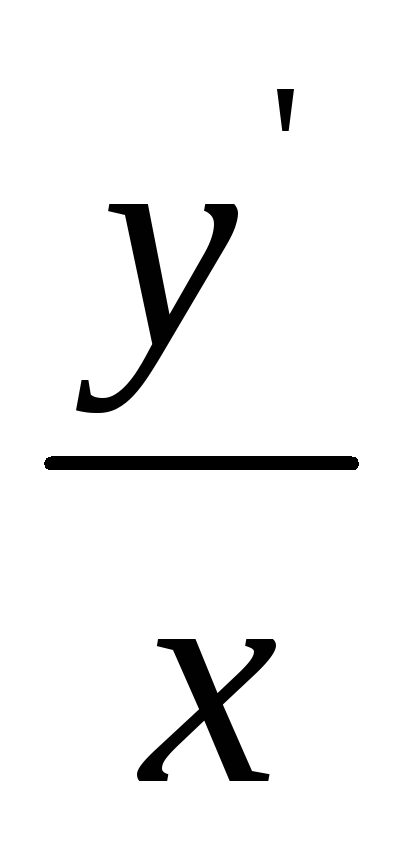 .
.
б) y![]() - 4y
- 4y![]() + 5y = 2x – 3 , y( 0 ) = 2, y
+ 5y = 2x – 3 , y( 0 ) = 2, y![]() (
0 ) = 0.
(
0 ) = 0.
-
а) (1 – y)y
 + 3(y
+ 3(y )
) =
0.
=
0.
б) y![]() - 4y
- 4y![]() + 3y = e
+ 3y = e![]() , y( 0 ) = 0, y
, y( 0 ) = 0, y![]() (
0 ) = 2.
(
0 ) = 2.
-
а) xy
 - (y
- (y )
) =
0.
=
0.
б) y![]() - 2y
- 2y![]() = x + 3 , y( 0 ) = 1, y
= x + 3 , y( 0 ) = 1, y![]() (
0 ) = 0.
(
0 ) = 0.
-
а) (y + 1)y
 - 3(y
- 3(y )
) =
0.
=
0.
б) y![]() - 2y
- 2y![]() + 2y = cos x , y( 0 ) = 0, y
+ 2y = cos x , y( 0 ) = 0, y![]() (
0 ) = 0.
(
0 ) = 0.
301-310. Найти общее решение системы линейных дифференциальных уравнений. Сделать проверку найденного решения.
301.
![]() 302.
302.
![]() 303.
303.
![]()
304.
![]() 305.
305.
![]() 306.
306.
![]()
307.
![]() 308.
308.
![]() 309.
309.
![]()
310.
![]()
Ряды
311 – 320. Выяснить, какие из данных рядов сходятся и какие расходятся.
-
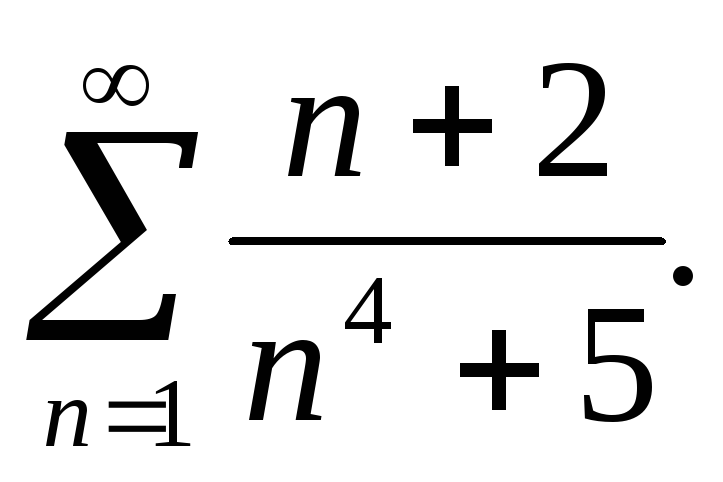 312.
312.
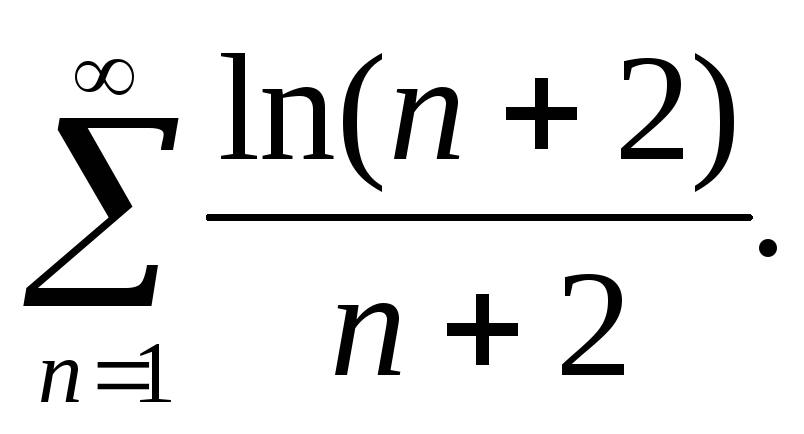 313.
313.
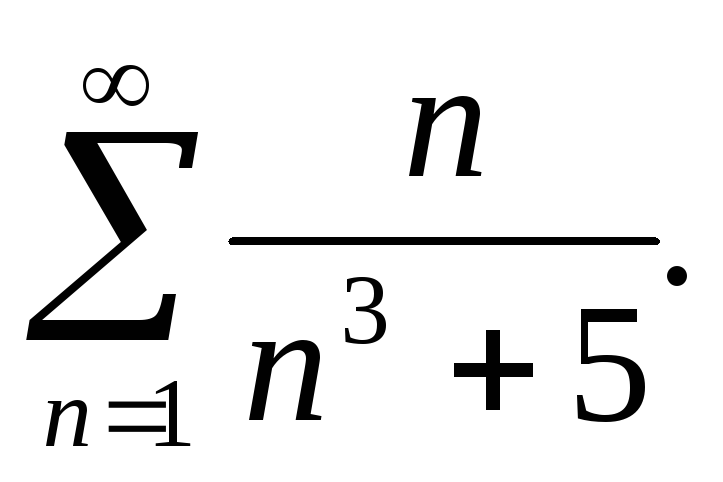 314.
314.
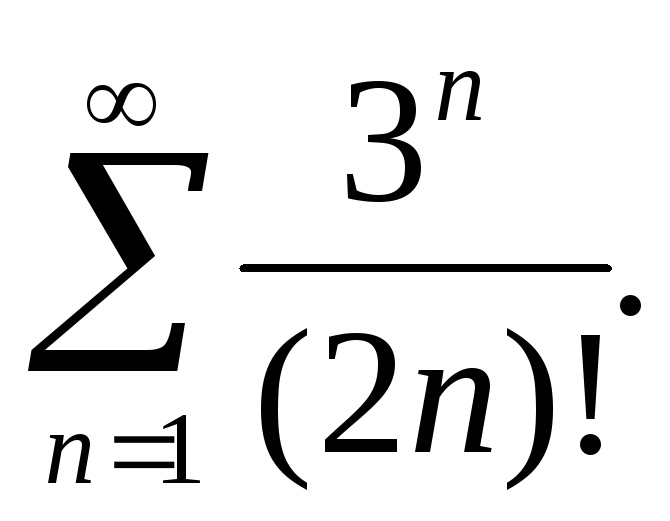
315.
![]() 316.
316.
![]() 317.
317.
![]() 318.
318.
![]()
319.
![]() 320.
320.
![]()
321 – 330. Определить область сходимости данных рядов.
321.
![]() 322.
322.
![]() 323.
323.
![]()
324.
![]() 325.
325.
![]() 326.
326.
![]()
327.
![]() 328.
328.
![]() 329.
329.
![]()
330.
![]()
331 - 340. Разложить функцию f(x) в ряд Фурье в указанном интервале. Выписать полученный ряд и три первых члена разложения отдельно. Построить график данной функции f(x), продолженной с данного интервала периодически на всю числовую ось.
331. f(x)
= x +1 в интервале
![]() .
.
332. f(x)
= x![]() +1 в интервале
+1 в интервале
![]() .
.
333. f(x)
=
![]() в интервале
в интервале
![]() .
.
334. f(x)
=![]() +1
в интервале
+1
в интервале
![]() .
.
335. f(x)
=![]() в интервале
в интервале
![]() .
.
336. f(x)
=![]() в интервале
в интервале
![]() .
.
337. f(x)
=
![]() в интервале
в интервале
![]() .
.
338. f(x)
= x -2 в интервале
![]() .
.
339. f(x)
= x![]() +1 в интервале
+1 в интервале
![]() .
.
340. f(x) =![]() в интервале
в интервале
![]() .
.
Операционное исчисление
341 - 350. Найти решения дифференциальных уравнений, удовлетворяющих заданным начальным условиям, применяя метод операционного исчисления. Сделать проверку найденного решения.
-
341. y
 - 3y
- 3y =t +1, y( 0 ) = 0, y
=t +1, y( 0 ) = 0, y (
0 ) = 1 .
(
0 ) = 1 .
342. y![]() - 4y
- 4y![]() + 3y = e
+ 3y = e![]() ,
y( 0 ) = 1, y
,
y( 0 ) = 1, y![]() (
0 ) = 0.
(
0 ) = 0.
343. y![]() - 6y
- 6y![]() + 9y = 5e
+ 9y = 5e![]() , y( 0 ) = -2, y
, y( 0 ) = -2, y![]() (
0 ) =0.
(
0 ) =0.
344. y![]() + 2y
+ 2y![]() + 10y = t
+ 10y = t![]() -
1 , y( 0 ) = 0, y
-
1 , y( 0 ) = 0, y![]() (
0 ) = 0.
(
0 ) = 0.
345. y![]() + 4y
+ 4y![]() + 3y = 2sin 3t , y( 0 ) = -3, y
+ 3y = 2sin 3t , y( 0 ) = -3, y![]() (
0 ) = 0.
(
0 ) = 0.
346. y![]() - 4y
- 4y![]() + 5y = -2t +1 , y( 0 ) = 1, y
+ 5y = -2t +1 , y( 0 ) = 1, y![]() (
0 ) = -1.
(
0 ) = -1.
347. y![]() + 9y = -3sin t , y( 0 ) = 2, y
+ 9y = -3sin t , y( 0 ) = 2, y![]() (
0 ) = 0.
(
0 ) = 0.
348. y![]() - 4y
- 4y![]() = e
= e![]() , y( 0 ) = 0, y
, y( 0 ) = 0, y![]() (
0 ) = -2.
(
0 ) = -2.
349. y![]() - 2y
- 2y![]() + 2 = t + 3 , y( 0 ) = -1, y
+ 2 = t + 3 , y( 0 ) = -1, y![]() (
0 ) = 0.
(
0 ) = 0.
350. y![]() - 2y
- 2y![]() + y = cos 2t , y( 0 ) = 0, y
+ y = cos 2t , y( 0 ) = 0, y![]() (
0 ) =3.
(
0 ) =3.
Двойные и тройные интегралы
151 – 160. Вычислить двойной интеграл по области D . Область интегрирования D изобразить на чертеже.
151.
![]() D : y = x2
, y = 2 – x2
.
D : y = x2
, y = 2 – x2
.
152.
![]() D : x = 1 , y = x2
, y = 0 .
D : x = 1 , y = x2
, y = 0 .
153.
![]() D : y = x , y = x3
, x
0 .
D : y = x , y = x3
, x
0 .
154.
![]() D : y = x2
, y =
D : y = x2
, y =
![]() .
.
155.
![]() D : x = 1 , y =
D : x = 1 , y =
![]() ,
y = -x2
.
,
y = -x2
.
156.
![]() D : x = 1 , y = x2
, y = 0 .
D : x = 1 , y = x2
, y = 0 .
157.
![]() D : y = x2
, y =
D : y = x2
, y =
![]() .
.
158.
![]() D : x = 1 , y =
D : x = 1 , y =
![]() y = -x3
.
y = -x3
.
159.
![]() D : y = x , y =
D : y = x , y =
![]() .
.
160.
![]() D : x = 1 , y = x2 , y = -
D : x = 1 , y = x2 , y = -![]() .
.
161 – 170. Вычислить с помощью тройного интеграла объем тела, ограниченного данными поверхностями. Сделать чертежи данного тела и его проекции на плоскость хОу .
161. z = 0 , z – x = 0 ,
y = 0 , y = 4 ,
![]()
-
z = 0 , z - 4
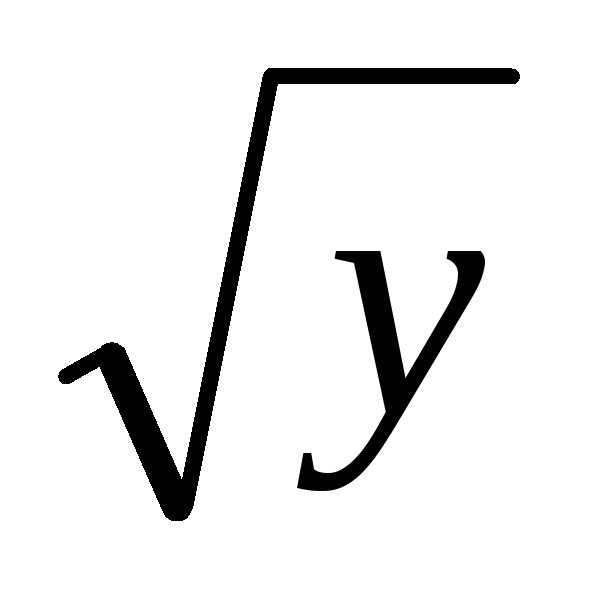 =
0 , x = 0 , x + y = 4 .
=
0 , x = 0 , x + y = 4 . -
z = 0 , z – 9 + y2 = 0 , x2 + y2 = 9 .
-
z = 0 , z – 1 + x2 = 0 , y = 0 , y = 3 – x .
-
z = 0 , y + z – 2 = 0 , x2 + y2 = 4 .
-
z = 0 , z – 1 + y2 = 0 , x = y2 , x = 2y2 + 1 .
-
z = 0 , 4z – y2 = 0 , 2x – y = 0 , x + y = 9 .
-
z = 0 , x2 + y2 – z = 0 , x2 + y2 = 4 .
-
z = 0 , z – y2 = 0 , x2 + y2 = 9 .
-
z = 0 , z – 4 + x + y = 0 , x2 + y2 = 4 .
351 – 360. Вычислить криволинейный интеграл. Сделать чертеж дуги кривой L.
351.
![]() ,
где L - отрезок прямой
от точки (1; 0) до точки (2;1).
,
где L - отрезок прямой
от точки (1; 0) до точки (2;1).
352 .
![]() ,
где L - отрезок прямой
от точки (1;1) до точки (2;2).
,
где L - отрезок прямой
от точки (1;1) до точки (2;2).
353.
![]() ,
где L - дуга кривой y
= ln (x + 1)от
точки (0; 0) до точки (e - 1;1).
,
где L - дуга кривой y
= ln (x + 1)от
точки (0; 0) до точки (e - 1;1).
354.
![]() ,
где L - дуга кривой y
= x
,
где L - дуга кривой y
= x![]() от точки (1;1) до точки (2;4).
от точки (1;1) до точки (2;4).
-
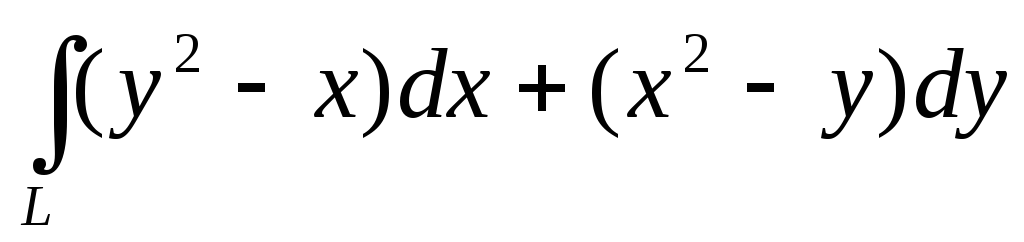 ,
где L - верхняя половина
окружности x = sin
2t,
,
где L - верхняя половина
окружности x = sin
2t,
y = cos 2t. Интегрировать против часовой стрелки.
-
 ,
где L - дуга кривой y
= x
,
где L - дуга кривой y
= x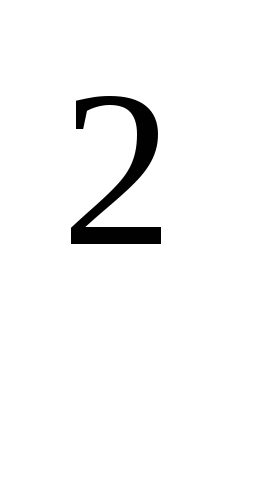 от точки (-1;1) до точки
от точки (-1;1) до точки
(-2;4).
-
 ,
где L - верхняя четверть
окружности x = 2sin
t,
,
где L - верхняя четверть
окружности x = 2sin
t,
y = 2cos t. Интегрировать против часовой стрелки.
358.
![]() ,
где L - отрезок прямой
от точки (1; 0) до точки (2;1).
,
где L - отрезок прямой
от точки (1; 0) до точки (2;1).
359.
![]() ,
где L - дуга кривой y
= x
,
где L - дуга кривой y
= x![]() от точки (1;1) до точки (2;4).
от точки (1;1) до точки (2;4).
360.
![]() ,
где L - верхняя половина
эллипса x = 3sin
2t, y = 4cos
2t. Интегрировать против
часовой стрелки.
,
где L - верхняя половина
эллипса x = 3sin
2t, y = 4cos
2t. Интегрировать против
часовой стрелки.
