3.1. Бистабильная ячейка

Триггер – схема (устройство) с двумя устойчивыми состояниями, переходящие из одного состояния в другое под действием внешнего сигнала и способное сохранить (сколь угодно долго) устойчивые состояния после снятия внешнего воздействия. Под термином “сколь угодно долго” подразумевается “до тех пор, пока включено питание устройства”.

В основе триггера лежит бистабильная ячейка – схема, которая может находиться только в двух устойчивых состояниях.

Два устойчивых состояния: первое Q=1, =0, второе Q=0,=1.

Состояния Q=1, =1 или Q=0,=0 внутренне противоречивы и не могут быть реализованы. Поэтому выходы так и обозначают: Q и Q с инверсией.

Триггер – управляемая бистабильная ячейка. Например на элементах ИЛИ-НЕ (хотя можно и на элементах И-НЕ):

S – Set (установка), R – Reset (сброс), при S=R=0 триггер превращается в не стабильную ячейку, сохраняющую своё состояние (это режим хранения информации).

S=1, R=0: ,

S=0, R=1: ,

При S=R=1 устанавливает Q==0, но после снятия внешнего воздействия триггер оказывается в неустойчивом (противоречивом) состоянии, поэтому он самопроизвольно может перейти в одно из двух устойчивых состояний: (Q=1,=0 или Q=0,=1).

Таким образом

S	R	Qn+1	Режим
0	0	Qn	хранение
1	0	1	запись 1
0	1	0	запись 0
1	1	-	не допускается

Логическая функция

Q_n+1=S + Q_n (при условии SR=0)

Условное обозначение

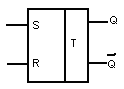
3.2. Физическая реализация триггера

Лучше понять работу триггера (и выяснить, что такое устойчивое и неустойчивое состояние), если обратиться к практической реализации, например, на биполярных транзисторах.

Вот пример бистабильной ячейки. Если один из транзисторов открыт, то другой закрыт, поэтому возможны только 2 устойчивых состояния.

Первое: Т1-закрыт ( потенциал его коллектора, выход Q и подаваемое на базу Т2 – высокое ), поэтому Т2 открыт, коллектор, а также выход и база Т1 – находятся под низким напряжением. Это состояние Q=1,=0.

Второе состояние: Т2 открыт. Проводя аналогичные рассуждения, получаем, что Т2 – закрыт, Q=0, =1.

Если как-то эту схему привести в состояние: Q==0 (т.е. оба транзистора открыты) или Q==1 (т.е. оба закрыты), то это состояние будет неустойчивым (да и противоречивым), т.к. открывание одного из транзисторов должно автоматически приводить к закрыванию второго транзистора. Состояние же, когда оба “полуоткрыты” – неустойчиво: малейшие изменения напряжений лавинообразно приведут схему в одно из устойчивых состояний.

Это триггер – управляемая бистабильная ячейка. R и S – входы, на них может подаваться входной сигнал, Q и - -выходы, с них снимается напряжение. Диоды поставлены, чтобы предотвратить короткое замыкание.

При S=R=0 схема превращается в обычную бистабильную ячейку, хранящую одно из двух состояний. При S=1, R=0 транзистор Т2 принудительно открывается (и устанавливается =0), Т1 закрывается (и устанавливается Q=1). Так происходит запись 1 (Q=1,=0).

При S=0, R=1 Т1 открывается (Q=0), Т2 закрывается (=1). Так происходит запись 0 (Q=0,=1). После снятия входного сигнала (S=R=0) триггер остается в том состоянии, в которое его привели.

Если подать одновременно S=R=1, оба транзистора откроются, установится состояние (Q==0). Из-за наличия диодов низкое напряжение на коллекторах не попадет на базы (и не произойдет короткого замыкания). Но после снятия входного напряжения, схема оказывается в неустойчивом состоянии и самопроизвольно переходит в одно из устойчивых состояний. То же самое происходит и при отключении схемы от источника питания (выключение компьютера): вся хранимая информация теряется и при включении питания в триггере самопроизвольно устанавливается одно из устойчивых состояний.

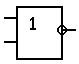
- реализует функцию «ИЛИ-НЕ» , то не трудно заметить, что в

схеме триггера две схемы «ИЛИ-НЕ», включены следующим образом:

Таким образом, получается логическая схема триггера, с которой и начиналось объяснение принципов его работы.