Линейные функции

Определение. Пусть V – линейное пространство над полем F. Функция называетсялинейной, если для любыхи.

Пример.

1. Нулевая функция: для любого.

2. Пусть (e₁,…,e_n) – базис. Тогда для любого x=xⁱe_i положим f(x)=xⁱ.

3. Пусть V - линейное пространство матриц. Тогда f(X)= X^T.

4. Пусть V – пространство многочленов степени не больше n. Тогда

f(P)= P(0) или f(P)= P`(0).

Теорема. Пусть (е₁,…,е_n) – базис пространства V. Тогда для любых , существует единая функцияf такая, что . Линейная функциязадается формулой:.

Линейные функции на V составляют линейное пространство: , гдеФункция– линейная (очевидно), 0 – нулевая функция, -f противоположная к f.

Определение. Сопряженным (двойственным) пространством V* для линейного пространства V называется пространство всех линейных функций на V с определенной выше операцией.

Пусть (е₁, … ,е_n) – базис в V. Определим линейные функции. Системаназывается сопряженным базисом для базиса (е₁, … ,е_n).

Теорема. Пусть (е₁, … ,е_n) – базис в V. Тогда:

1. Сопряженный базис (е₁, … ,е_n) существует;

2. Сопряженный базис (е₁, … ,е_n) единственен;

3. В самом деле является базисом в V*;

4. Координатами любой функции 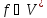в базисе (е₁, … ,е_n) являются числа f (е₁), … , f (е_n);

5. dim V = dim V*.

Определение. Ядром функции называется следующее множество:

Теорема. Для любого конечномерного пространства V и любой линейной функции справедливы следующие утверждения:

1. Ядро является подпространством вV;

2. Если функция f не является нулевой, то

Теорема. Пусть Е = (е₁, … ,е_n) – базис линейного пространства V. Тогда справедливы следующие утверждения:

1. Множество U всех векторов x, координаты которых в базисе удовлетворяют линейной однородной системе

(1)

является подпространством в V и dimU=n-rank()_{m x n} .

2. Всякое k-мерное пространство U пространства V состоит из всех векторов, координаты которых удовлетворяют некоторой однородной линейной системе.

Теорема. Пусть V – n-мерное линейное пространство. Тогда функция заданная формулойдля любой функции, является линейной, то есть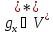. Отображение, заданное по правилуявляется естественным изоморфизмом пространств.

Двойственное пространство и двойственный базис

Определение. Пусть V – векторное пространство над полем F. Двойственным векторным пространством к V называется векторное пространство линейных функционалов , то есть множество линейных функционалов  , с операциями сложения и умножения на скаляр, определенными формулами:

1. для всех ;

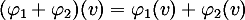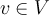2.  для всех .

Двойственное пространство к пространству обозначают через  . Таким образом, .

Замечание. Отображение такое, что для всех  и  является спариванием между и .

Пусть — векторное пространство размерности с базисом . Тогда линейные функционалы , определенные соотношением

,

образуют базис .

Определение. Базис пространства , указанный в формулировке

предложения 1, называется двойственным к базису пространства .