Пересечение и сумма подпространств

Пусть U и W — подпространства векторного пространства V над полем F.

Предположим, пересечение подпространств U и W является векторным пространством.

Замечание.Объединение 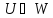пространств U и W не обязано быть векторным пространством, как показано в следующем примере.

Пример. Пусть , то есть множество векторов вида , где . Базисом этого пространства служат вектора e₁=(1,0) и e₂=(0,1). Положим U₁=и U₂=– линейные оболочки векторов и, соответственно. Сумма векторовне содержится в

Определение. Суммой подпространств U и W называется наименьшее подпространство в V, содержащее U и W, то есть

.

Вообще говоря, можно определить сумму любого конечного числа подпространств:

Сумма подпространства U₁, U₂, …, U_n в V - это наименьшее подпространство, содержащее все U_i , то есть

Пусть U и W – подпространства конечномерного векторного пространства V. Тогда

Прямая сумма

1)Внешняя прямая сумма

Пусть U и W — векторные пространства над полем F.

Определение. Прямой суммой векторных пространств U и W  называется декартово произведение V=U×W с операциями сложения векторов и умножения их на скаляр, определенными следующей формулой:

Замечание. Определенная таким образом прямая сумма называется внешней. Непосредственной проверкой можно убедиться, что внешняя прямая сумма векторных пространств является векторным пространством.

Предположим, внешняя прямая сумма пространствU и W обладает следующим свойством: если и— линейные отображения, определенные условиямитоявляется внутренней прямой суммой подпространств. Таким образом,

2) Внутренняя прямая сумма

Определение. Пространство V называется прямой суммой своих векторных подпространств U₁, U₂, …, U_n , если каждый векторможет быть представлен одним и только одним способом в виде суммы

, где

Прямая сумма векторных пространств обозначается через V =.

Определенная таким образом прямая сумма называется внутренней.

Пример. Пусть  и подпространства U₁ и U₂ определены так же, как в примере 1. Тогда сумма является прямой, то есть V =.

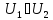Сумма V =является прямой тогда и только тогда, когда выполнено любое из следующих двух условий:

1);

2) dim V = dim + dim + …+ dim.

Следствие. Если n=2, то сумма V =является прямой тогда и только тогда, когда=0.

Для любого m-мерного подпространства U векторного пространства V размера n найдется такое n – m – мерное пространство W, такое что V =.

Фактор пространства

Пусть L – линейное пространство. - его подпространство. Определим на L отношение эквивалентности следующим образом: x~y ↔ x-yM, а- вектор. Различные вопросы приводят к рассмотрению множеств вида:

,

“сдвигов” линейного пространства M на вектор l. Такие сдвиги не обязаны быть линейными подпространствами в L; их называют линейными подмногообразиями.

Лемма. тогда и только тогда, когда и . Таким образом, всякое линейное подмногообразие однозначно определяет линейное подпространство M, сдвигом которого оно является. Вектор же сдвига определяется с точностью до элемента из этого подпространства.

Определение. Фактором пространства L/M линейного пространства L по M называется множество всех линейных подмногообразий в L, являющихся сдвигами подпространства M, со следующими операциями:

а)

б)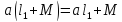для любых.

Эти операции определены корректно и превращают L/M в линейное пространство над полем .

Замечание.

а) Из определения видно, что аддитивная группа L/M совпадает с факторгруппой аддитивной группы L по аддитивной группе M. В частности, подмногообразие является нулем вL/M.

б) Имеется каноническое отображение Оно сюръективно, а его слои – прообразы элементов – суть как раз подмногообразия, отвечающие этим элементам.

Следствие. Если L конечномерно, то dim L/M = dim L - dim M.