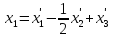Линейные формы
.docx1. Линейные формы.
Пусть в линейном пространстве
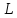 задана
числовая функция векторного аргумента.
То есть каждому вектору
задана
числовая функция векторного аргумента.
То есть каждому вектору
 поставлено
в соответствие число
поставлено
в соответствие число
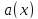 .
Пусть
.
Пусть
 – множество всех базисов пространства
– множество всех базисов пространства
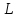 .
Мы
можем рассмотреть функцию
.
Мы
можем рассмотреть функцию
 ,
где
,
где
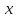 ∈
∈
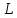 ,
e
∈
,
e
∈
 .
Мы
получим обычную (инвариантную) функцию
.
Мы
получим обычную (инвариантную) функцию
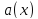 ,
если
,
если
 .
.
Определение.
Функция
 называется
линейной, если:
a)
называется
линейной, если:
a)
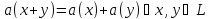 (условие
аддитивности).
б)
(условие
аддитивности).
б)
 (условие
однородности).
В
качестве значений функции
(условие
однородности).
В
качестве значений функции
 будем
брать действительные числа, если L
– действительно и будем брать комплексные
числа, если L
–
комплексно.
будем
брать действительные числа, если L
– действительно и будем брать комплексные
числа, если L
–
комплексно.
Пример
Пусть
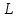 –
пространство многочленов степени не
выше
–
пространство многочленов степени не
выше
 .
.
Пусть
каждому многочлену из
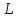 ставится в соответствие число
ставится в соответствие число
 по
формуле:
по
формуле:
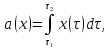 (1)
(1)
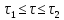
условия
a)
и
b)
выполняются вследствие известных
свойств определённого интеграла. Значит
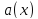 является линейной в
является линейной в
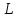 .
Рассмотрим
.
Рассмотрим
 (2)
(2)
Обозначим
через
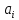 функцию
функцию
 на базисном векторе
на базисном векторе
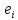 :
:
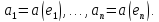 (3)
(3)
Если
базис фиксирован, то
 - вполне определённые числа. Подставив
(3) в (2) получим выражение функции
- вполне определённые числа. Подставив
(3) в (2) получим выражение функции
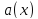 в
виде однородного
многочлена первой степени относительно
координат
вектора
в
виде однородного
многочлена первой степени относительно
координат
вектора :
:
 .
(4)
.
(4)
Однородные
многочлены степени
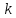 принято
называть формами
степени k. При
принято
называть формами
степени k. При
 употребляют
термин “линейные формы”, при
употребляют
термин “линейные формы”, при
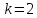 ,
термин “квадратичные формы”.
,
термин “квадратичные формы”.
Теорема 1
Множество
 всех линейных функций, заданных в
пространстве L представляет собой
линейное пространство.
всех линейных функций, заданных в
пространстве L представляет собой
линейное пространство.
Определение
Линейное
пространство
 всех линейных функций, определённых на
L
называется сопряжённым пространству
L.
всех линейных функций, определённых на
L
называется сопряжённым пространству
L.
Теорема 2
Если линейное пространство n-мерно, то сопряжённое вниз пространство также n-мерно.
2. Билинейные формы.
Числовая
функция
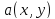 двух
векторных аргументов
двух
векторных аргументов
 называется
билинейной,
если она линейна по каждому аргументу.
То есть:
называется
билинейной,
если она линейна по каждому аргументу.
То есть:

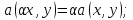
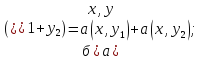
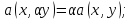
Здесь
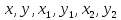 –
любые векторы пространства
–
любые векторы пространства
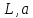 – произвольное число.
– произвольное число.
Пусть
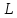 –
линейное
–
линейное
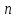 –
мерное пространство,
–
мерное пространство,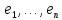 – базис в нём. И пусть аргументы билинейной
функции разложены по этому базису
– базис в нём. И пусть аргументы билинейной
функции разложены по этому базису
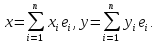
Тогда:
 (1)
(1)
Введём обозначения:
 (2)
(2)
Тогда получим:
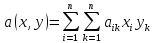 (3)
(3)
Формула
(3) выражает функцию
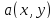 в
координатах по данному базису.
в
координатах по данному базису.
Множество всех билинейных форм, заданных в линейном пространстве L, образует линейное пространство.
Определение
Билинейная
форма
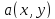 называется
симметричной,
называется
симметричной,
если
 следует
следует
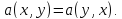
3. Матрица билинейной формы.
Пусть дана произвольная билинейная форма:




 –
матрица
билинейной формы.
–
матрица
билинейной формы.
Определение
Рангом билинейной формы называется ранг её матрицы.
4. Квадратичные формы. Закон инерции квадратичных форм. Сигнатура.
Пусть
билинейная форма
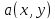 является
симметричной
является
симметричной
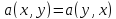 .
Это равносильно тому, что в любом базисе
симметрична её матрица
.
Это равносильно тому, что в любом базисе
симметрична её матрица
 –
транспонированная
для A
матрица.
–
транспонированная
для A
матрица.
В самом деле:
 .
.
Если
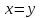 ,
то
,
то

Функция
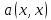 называется квадратичной формой,
отвечающей данной симметричной форме
называется квадратичной формой,
отвечающей данной симметричной форме

Основная теорема о квадратичных формах
Всякая квадратичная форма может быть приведена некоторым невырожденным линейным преобразованием к каноническому виду.
Назовём нормальным видом квадратичной формы сумму квадратов нескольких неизвестных с коэффициентами +1 или -1.
Всякую действительную квадратичную форму F можно привести невырожденным линейным преобразованием с действительными коэффициентами к нормальному виду.
Теорема (закон инерции действительных квадратичных форм)
Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится данная квадратичная форма с действительными коэффициентами действительным линейным невырожденным преобразованием не зависит от выбора этого преобразования.
Число положительных квадратов в той нормальной форме, к которой приводится данная действительная квадратичная форма f , называется положительным индексом инерции этой формы, число отрицательных квадратов – отрицательным индексом инерции, а разность между положительным и отрицательным индексами инерции – сигнатурой формы f .
Теорема
Две квадратичные формы от n – неизвестных с действительными коэффициентами тогда и только тогда переводятся друг в друга невырожденными действительными линейными преобразованиями, если эти формы имеют одинаковые ранги и одинаковые сигнатуры.
5. Положительно и отрицательно определённые квадратичные формы. Критерий Сильвестра для положительно определённых и отрицательно определённых квадратичных форм.
Квадратичная
форма A,
определённая в действительном линейном
пространстве
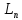 называется положительно
(отрицательно) определённой,
если:
называется положительно
(отрицательно) определённой,
если:
∀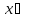
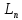 ,
,
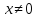
A > 0 (A <0)
Пусть
 матрица
квадратичной формы
матрица
квадратичной формы
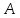 .
.
 – последовательность
главных миноров матрицы
– последовательность
главных миноров матрицы
 .
.
Критерием положительной определённости квадратичной формы является определенный критерий.
Критерий Сильвестра
Для
того, чтобы квадратичная форма A
была положительно определённой необходимо
и достаточно, чтобы все главные миноры
её матрицы
 были положительны
были положительны
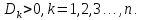
Для того, чтобы квадратичная форма A была отрицательно определённой необходимо и достаточно, чтобы:
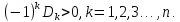
Пример
Выяснить,
является ли положительно определённой
или отрицательно определённой квадратичная
форма

Запишем матрицу:
 .
.
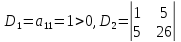 =1>0.
=1>0.
Согласно критерию Сильвестра данная квадратичная форма принимает только положительные значения.
Пример
Определить какие квадратичные формы являются положительно, либо отрицательно определёнными:


а) Запишем матрицу:
 .
.
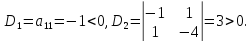
Квадратичная форма является отрицательно определённой.
б) Запишем матрицу:
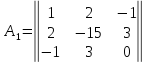
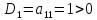 ,
,
 ,
,
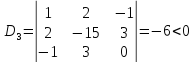 .
.
Квадратичная форма общего вида.
Приведение квадратичной формы к каноническому виду методом Лагранжа, Якоби и ортогональным преобразованием.
Метод Лагранжа
Каждую квадратичную форму с помощью невырожденного линейного преобразования можно привести к каноническому виду.
Пример 1
Дана
квадратичная форма
 .
Привести ее к каноническому виду методом
Лагранжа, записав соответствующие
преобразования переменных.
.
Привести ее к каноническому виду методом
Лагранжа, записав соответствующие
преобразования переменных.
Коэффициент
при
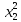 равен 3,
3≠0.
Выделим в квадратичной форме члены,
содержащие
равен 3,
3≠0.
Выделим в квадратичной форме члены,
содержащие

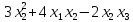 .
.
Дополним до полного квадрата членами, не содержащими x2, и сразу вычтем

Введем
обозначение
 исходя из принципа:
исходя из принципа:
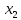 в квадратичной форме пропадает, а
в квадратичной форме пропадает, а
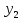 в квадратичной форме появляется. Приводя
подобные члены, перепишем квадратичную
форму
в квадратичной форме появляется. Приводя
подобные члены, перепишем квадратичную
форму

К
квадратичной форме
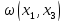 снова применим метод выделения полного
квадрата.
снова применим метод выделения полного
квадрата.
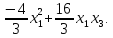
Дополним
это выражение до полного квадрата
членами, не содержащими
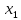
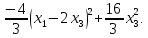
Обозначим
 через
через
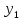 .
Приводя подобные, перепишем исходную
квадратичную форму
.
Приводя подобные, перепишем исходную
квадратичную форму
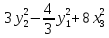 .
.
Выделять снова полный квадрат уже не надо.
Обозначим
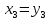 .
Получим следующий канонический вид
квадратичной формы
.
Получим следующий канонический вид
квадратичной формы
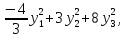 где
где
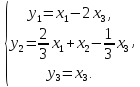
Запишем преобразование переменных в матричной форме
 ·X
.
·X
.
Пример 2
Найти
канонический вид и невырожденное
преобразование переменных, приводящее
к этому виду квадратичную форму
 .
.
Так как в этой форме отсутствуют квадраты, то
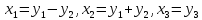 (1)
(1)
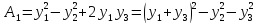
Применив
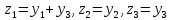 (2)
(2)
получим канонический вид формы
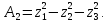
Из
(2) найдем

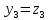 .
.
Подставляя эти выражения в (1) получим искомое преобразование

Метод Якоби
Пример 1
Для применения этого метода квадратичная форма
 (1)
(1)
должна удовлетворять некоторым специальным условиям.
Пусть
квадратичная форма (1) имеет ранг
 и миноры, стоящие в левом верхнем углу
матрицы формы от 1-го до -го порядка
отличны от нуля
и миноры, стоящие в левом верхнем углу
матрицы формы от 1-го до -го порядка
отличны от нуля
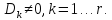 (2)
(2)
Тогда канонический вид формы (1) можно найти по формуле Якоби
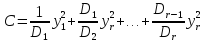 (3)
(3)
Ортогональное преобразование
Квадратичная
матрица
 является
ортогональной,
если ее элементы действительны и
выполняется одно из пяти следующих
эквивалентных свойств:
является
ортогональной,
если ее элементы действительны и
выполняется одно из пяти следующих
эквивалентных свойств:
-
Строки образуют ортонормированную систему;
-
Столбцы образуют ортонормированную систему;
-
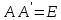 ;
; -
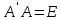 ;
; -
 – транспонированная
матрица для
– транспонированная
матрица для
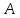 ;
;
Рассмотрим n-квадратичную форму
 (1)
(1)
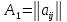 квадратичной
формы (1) симметрична. Она может быть
представлена в виде
квадратичной
формы (1) симметрична. Она может быть
представлена в виде
 ,
,
где
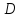 – диагональная матрица, на диагонали
которой стоят собственные числа матрицы
– диагональная матрица, на диагонали
которой стоят собственные числа матрицы
 ,
а
,
а
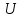 –
ортогональная матрица. Столбцы матрицы
–
ортогональная матрица. Столбцы матрицы
 являются координатами некоторого
ортонормированного базиса
являются координатами некоторого
ортонормированного базиса
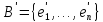 ,
в котором
,
в котором
 имеет диагональный вид
имеет диагональный вид
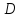 и следовательно квадратичная форма –
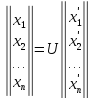
искомый канонический вид. Соответствующие
преобразования координат определяются
соответствием
и следовательно квадратичная форма –
искомый канонический вид. Соответствующие
преобразования координат определяются
соответствием
Пример 1
Найти
ортогональное преобразование, приводящее
квадратичную форму
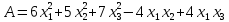 ,
заданную в евклидовом пространстве
,
заданную в евклидовом пространстве
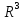 к каноническому виду. Написать этот
канонический вид.
к каноническому виду. Написать этот
канонический вид.

Находим собственные числа этой матрицы
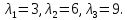
Находим соответствующие собственные ортонормированные векторы

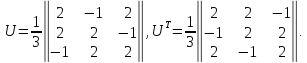
В
базисе
 заданная квадратичная форма имеет вид:
заданная квадратичная форма имеет вид:
 ,
,
а соответствующее преобразование координат будет таким:
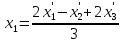


Пример 2
Найти
ортогональное преобразование, приводящее
квадратичную форму 11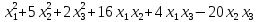 к каноническому виду. Написать этот
канонический вид.
к каноническому виду. Написать этот
канонический вид.

Находим собственные числа этой матрицы

Находим соответствующие собственные ортонормированные векторы
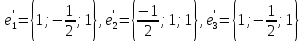
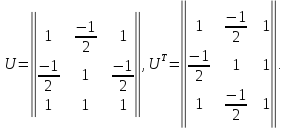
В
базисе
 заданная квадратичная форма имеет вид:
заданная квадратичная форма имеет вид:
 ,
,
а соответствующее преобразование координат будет таким: