
Лекция №29 Понятие λ-матрицы.
Определение
λ-матрица — квадратная матрица, элементами которой являются многочлены над некоторым числовым полем. Если имеется некоторый элемент матрицы, который является многочленом степени l, и нет элементов матрицы степени большей чем l, то l — степень λ-матрицы.
 ,
,
 (1)
(1)
Используя обычные операции над матрицами, любую λ-матрицу можно представить в виде:
 (2)
(2)
В
случае если определитель матрицы  отличен
от нуля, то λ-матрица называется регулярной.
отличен
от нуля, то λ-матрица называется регулярной.
Пример
 (3)
(3)
Теорема о приведении λ-матрицы к каноническому виду
Всякая
λ-матрица эквивалентна некоторой
канонической
 -матрице,
то есть она приводится элементарными
преобразованиями к каноническому виду.
-матрице,
то есть она приводится элементарными
преобразованиями к каноническому виду.
Доказательство
Будем доказывать эту теорему методом математической индукции. Действительно, при n=1 будет
 (4)
(4)
Если
 ,
то наша матрица уже каноническая. Если
же
,
то наша матрица уже каноническая. Если
же ,
то достаточно разделить многочлен
,
то достаточно разделить многочлен на его старший коэффициент – это будет
элементарное преобразование матрицы
– и мы получим каноническую матрицу.
на его старший коэффициент – это будет
элементарное преобразование матрицы
– и мы получим каноническую матрицу.
Пусть
теорема уже доказана для λ-матриц порядка
 .
Рассмотрим произвольную λ-матрицу
.
Рассмотрим произвольную λ-матрицу порядкаn.
Если
она нулевая, то уже является канонической.
Поэтому будем считать, что среди элементов
матрицы
порядкаn.
Если
она нулевая, то уже является канонической.
Поэтому будем считать, что среди элементов
матрицы
 имеются ненулевые.
имеются ненулевые.
Переставляя
строки и столбцы матрицы
 ,
можно перевести один из ненулевых
элементов в левый верхний угол. Таким
образом, среди λ-матриц, эквивалентных
матрице
,
можно перевести один из ненулевых
элементов в левый верхний угол. Таким
образом, среди λ-матриц, эквивалентных
матрице ,
имеются такие, в левом верхнем углу
которых стоит ненулевой многочлен.
Рассмотрим все такие матрицы. Можно
найти среди всех λ-матриц, эквивалентных
матрице
,
имеются такие, в левом верхнем углу
которых стоит ненулевой многочлен.
Рассмотрим все такие матрицы. Можно
найти среди всех λ-матриц, эквивалентных
матрице и имеющих ненулевой элемент в левом
верхнем углу, одну из таких, что многочлен,
стоящий в её левом верхнем углу, имеет
наименьшую возможную степень. Деля
первую строку этой матрицы на старший
коэффициент указанного многочлена, мы
получим такую λ-матрицу, эквивалентную
матрице
и имеющих ненулевой элемент в левом
верхнем углу, одну из таких, что многочлен,
стоящий в её левом верхнем углу, имеет
наименьшую возможную степень. Деля
первую строку этой матрицы на старший
коэффициент указанного многочлена, мы
получим такую λ-матрицу, эквивалентную
матрице ,
,
 ,
(5)
,
(5)
что
 ,
старший коэффициент этого многочлена
равен 1.
,
старший коэффициент этого многочлена
равен 1.
Докажем,
что все элементы первой строки и первого
столбца полученной матрицы нацело
делятся на
 .
Пусть для
.
Пусть для
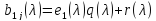 ,
(6)
,
(6)
где
степень
 меньше степени
меньше степени ,
если
,
если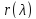 отлично от нуля. Тогда, вычитая изj-го
столбца матрицы первый столбец, умноженный
на
отлично от нуля. Тогда, вычитая изj-го
столбца матрицы первый столбец, умноженный
на
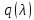 ,
а затем переставляя первый иj-й
столбцы, мы придём к матрице, эквивалентной
матрице
,
а затем переставляя первый иj-й
столбцы, мы придём к матрице, эквивалентной
матрице
 ,
в левом верхнем углу которой стоит
многочлен
,
в левом верхнем углу которой стоит
многочлен ,
то есть многочлен меньшей степени, чем
,
то есть многочлен меньшей степени, чем ,
что противоречит выбору этого многочлена.
Отсюда следует
,
что противоречит выбору этого многочлена.
Отсюда следует ,
что и требовалось доказать.
,
что и требовалось доказать.
Вычитая
теперь из j-го
столбца первый столбец, умноженный на
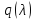 ,
заменим элемент
,
заменим элемент нулём. Делая такие преобразования дляj=2,
3, … , n,
заменим
нулями все элементы
нулём. Делая такие преобразования дляj=2,
3, … , n,
заменим
нулями все элементы
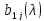 .
Аналогично заменяются нулями все
элементы
.
Аналогично заменяются нулями все
элементы Следовательно, мы придём к такой матрице,
эквивалентной матрице
Следовательно, мы придём к такой матрице,
эквивалентной матрице ,
в левом верхнем углу которой стоит
многочлен
,
в левом верхнем углу которой стоит
многочлен ,
а все остальные элементы первой строки
и первого столбца равны нулю,
,
а все остальные элементы первой строки
и первого столбца равны нулю,
 (7)
(7)
По индуктивному предположению, матрица (n-1)-го порядка, стоящая в правом нижнем углу полученной матрицы (7), элементарными преобразованиями приводится к каноническому виду:
 (8)
(8)
Совершив эти же преобразования, мы получим, что
 (9)
(9)
Теорема об эквивалентности двух λ-матриц
Всякая λ-матрица эквивалентна лишь одной канонической матрице.
Доказательство
Пусть
дана произвольная λ-матрица А(λ)
порядка
n.
Фиксируем некоторое натуральное число
k,
 ,и
рассмотрим
все миноры k-го
порядка матрицы А(λ).
Вычисляя эти миноры, получим конечную
систему многочленов от λ; наибольший
общий делитель этой системы многочленов,
взятый со старшим коэффициентом 1,
обозначим через
,и
рассмотрим
все миноры k-го
порядка матрицы А(λ).
Вычисляя эти миноры, получим конечную
систему многочленов от λ; наибольший
общий делитель этой системы многочленов,
взятый со старшим коэффициентом 1,
обозначим через
 .
.
Получили многочлены
 (10)
(10)
однозначно
определяемые самой матрицей А(λ).
При
этом
 есть наибольший общий делитель всех
элементов матрицы А(λ),
взятый с коэффициентом 1, а
есть наибольший общий делитель всех
элементов матрицы А(λ),
взятый с коэффициентом 1, а
 равен определителю матрицы А(λ),
делённому на его старший коэффициент.
Если матрица А(λ)
имеет ранг r,
то
равен определителю матрицы А(λ),
делённому на его старший коэффициент.
Если матрица А(λ)
имеет ранг r,
то
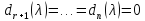 ,
(11)
,
(11)
в то время как все остальные многочлены системы (10) отличны от 0.
Определение
Наибольший
общий делитель
 всех миноров k-го
порядка λ-матрицы А(λ),
k=1,
2, …, n,
не
меняется при выполнении в матрице А(λ)
элементарных преобразований.
всех миноров k-го
порядка λ-матрицы А(λ),
k=1,
2, …, n,
не
меняется при выполнении в матрице А(λ)
элементарных преобразований.
Пусть
к i-ой
строке матрицы А(λ)
прибавляется её j-я
строка, j≠i,
умноженная
на многочлен φ(λ);
получающуюся матрицу обозначим через
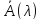 ,
а наибольший общий делитель всех её
миноров
k-го
порядка, взятый со старшим коэффициентом
1 – через
,
а наибольший общий делитель всех её
миноров
k-го
порядка, взятый со старшим коэффициентом
1 – через
 .
.
Ясно,
что не будут меняться те миноры, через
которые i-я
строка не проходит. Не меняются и те
миноры, через которые проходят как i-я,
так и j-я
строки, так как определитель не меняется
от прибавления к одной его строке
кратного другой его строки. Возьмём
любой из тех миноров k-го
порядка, через которые проходит i-я
строка, но не проходит j-я;
обозначим его через M.
Соответствующий минор матрицы
 можно представить, как сумму минораМ
и
умноженного на φ(λ)
минора М’
матрицы А(λ),
получающегося
из минора М
заменой элементов i-ой
строки матрицы А(λ)
соответствующими элементами её j-ой
строки. Так как М
и М’
делятся
на
можно представить, как сумму минораМ
и
умноженного на φ(λ)
минора М’
матрицы А(λ),
получающегося
из минора М
заменой элементов i-ой
строки матрицы А(λ)
соответствующими элементами её j-ой
строки. Так как М
и М’
делятся
на
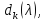 то иМ+
φ(λ)М’ будет
делиться на
то иМ+
φ(λ)М’ будет
делиться на
 .
Отсюда следует, что все миноры матрицы
.
Отсюда следует, что все миноры матрицы нацело делятся на
нацело делятся на ,
а поэтому и
,
а поэтому и делится на
делится на .
Так как для рассматриваемого элементарного
преобразования существует обратное
того же типа, то и
.
Так как для рассматриваемого элементарного
преобразования существует обратное
того же типа, то и делится на
делится на .
Если учесть, что старшие коэффициенты
обоих многочленов равны 1, то
.
Если учесть, что старшие коэффициенты
обоих многочленов равны 1, то ,
что и требовалось доказать.
,
что и требовалось доказать.
