Примечание

При определении скорости и ускорения переносного движения МТ в некоторых случаях удобно воспользоваться формулами (7.5), (7.13):

Здесь — скорость и ускорение начала подвижной системы координат О,

— скорость и ускорение МТ при ее движении относительно начала подвижной системы координат О.

Пример 1

2 МТ спускается из состояния покоя с постоянным относительно призмы ускорением 5 см/с² вдоль наклонной грани призмы, двигающейся вправо из состояния покоя с постоянным ускорением 3 см/с², (рис. 68).

Определить абсолютные скорость и ускорение МТ в момент времени t (при условии, что она в этот момент находится на призме).

Рис. 68

Движение МТ относительно неподвижной системы координат Oxy будет абсолютным ().

Прямолинейное равноускоренное движение МТ из состояния покоя относительно призмы будет относительным, т. е., W_r=5 cм/c², V_r0=0.

Поступательное равноускоренное движение МТ вместе с призмой из состояния покоя относительно неподвижной системы координат Оxy будет переносным, т. е. W_e=3 cм/c², V_e0=0.

На рис. 68 изображено положение МТ в момент времени t.

3

4б Относительное движение МТ – прямолинейное равноускоренное W_r=5 cм/c² , V_r0=0.

5б K01 KMT(P)

7б V_r=V_r0+W_rt=5t см/c.

Относительное скорость и ускорение МТ изображены на рис. 69.

6б Переносное движение МТ — поступательное равно-ускоренное движение призмы с ускорением W_e=3 cм/c², V_e0=0.

7б K01 KMT(P)

7б V_е=V_е0+W_еt=3t см/c.

Переносные скорость и ускорение МТ изображены на рис. 69.

Рис. 69

8 Так как переносное движение МТ поступательное, т.е. _e=0, то W_К=0.

9а Не заданы ни уравнения движения, ни кинематические параметры абсолютного движения МТ: V_a=?, W_a=?

11 Используя правило параллелограмма и теорему косинусов, получим:

Абсолютные скорость и ускорение МТ изображены на рис. 69.

12 Ответ: V_a=7t см/c, W_a=7 см/с².

Пример 2

2 Платформа перемещается в горизонтальной плоскости по закону x=3t² м. МТ находится на платформе и перемещается по окружности радиуса  = 2м и при этом центральный угол BО₁B₀ изменяется по закону:

(рис. 70).

Рис. 70

Определить для МТ абсолютную скорость V_a и ускорение W_a в момент времени t₁=1 c.

Движение МТ относительно неподвижной системы координат Oxy будет абсолютным (). Вращательное движение МТ по окружности относительно платформы будет относительным, т. е. .

Поступательное движение МТ вместе с платформой относительно неподвижной системы координат Oxy будет переносным, т. е. х_е=3t² м.

Положение МТ в момент времени t₁=1c определяется параметрами:

(рис. 71).

3

Рис. 71

4в Относительное движение МТ — вращательное движение МТ по окружности по закону .

5

в К03 ВДТ

8в

9

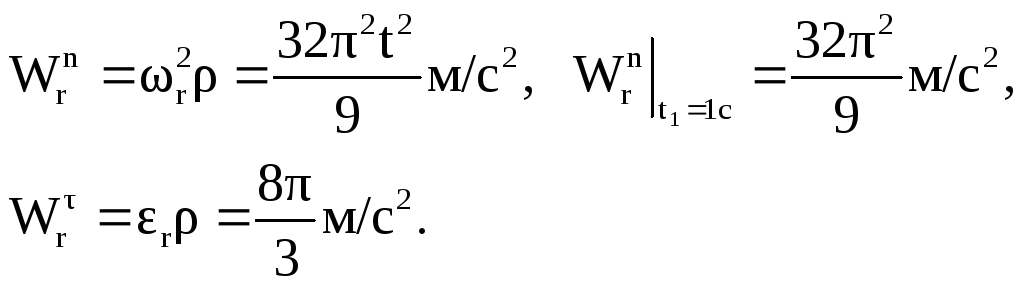
Относительная скорость и составляющие относительного ускорения МТ изображены на рис. 71.

6б Переносное движение МТ поступательное по закону x_e=3t² м.

7

5б

8б .

б К01 КМТ

Переносная скорость и ускорение МТ изображены на рис. 71.

8 Так как переносное движение МТ поступательное, т. е. _е=0, то W_К=0.

9а Не заданы ни уравнения движения, ни кинематические параметры абсолютного движения МТ: V_a=?, W_a=?

11 Проектируем уравнения 3 на оси неподвижной системы координат Оху:

12

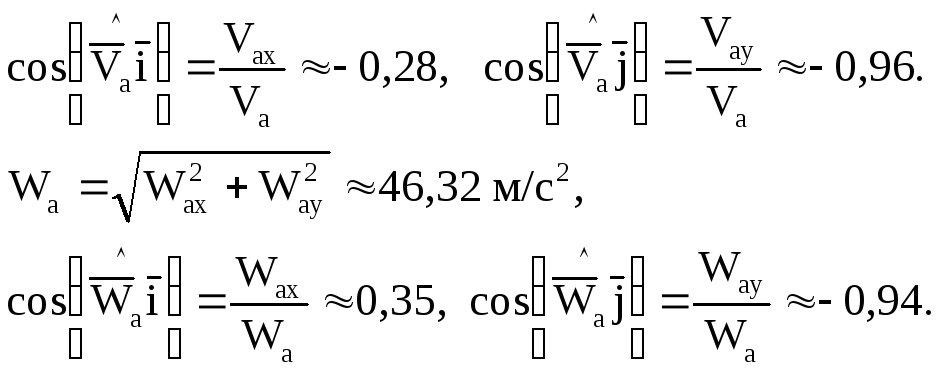
Ответ:

Пример 3

2 Диск радиуса =24 см вращается вокруг горизонтальной оси Оу по закону =0,15t² в направлении, указанном на рис. 72. По диаметру DЕ диска совершает колебательные движения точка В по закону:

Рис. 72

Определить абсолютную скорость и ускорение МТ в момент времени t₁=3,5 c.

Движение МТ относительно неподвижной системы координат Oxyz будет абсолютным ().

Прямолинейное колебательное движение МТ по диаметру DЕ относительно диска будет относительным, т. е.

Движение МТ вместе с диском, вращающимся относительно оси Оу неподвижной системы координат Oxyz, будет переносным, т. е. _е=0,15 t².

Положение МТ на диске в момент времени t₁=3,5 c определяется параметром см (рис. 73).

3

4б Относительное движение МТ – прямолинейное колебательное по закону

5

6в

.

б К01 КМТ

7в

8в .

9в

Относительные скорость и ускорение МТ направлены по диаметру и изображены на рис. 73.

6в Переносное движение МТ вращательное по закону _е=0,15 t².

8в

7в К03 ВДТ

Угловые скорость и ускорение изображены на рис. 73.

9

Переносная скорость и касательная составляющая переносного ускорения МТ перпендикулярны плоскости диска, а нормальная составляющая переносного ускорения МТ направлена по кратчайшему расстоянию от этой МТ до оси Оу (рис. 73).

8 .

Используя определение векторного произведения, с учетом рис. 73 получим:

Ускорение перпендикулярно и (т. е. направлено перпендикулярно плоскости диска и параллельно оси Ох) и направлено в ту сторону, чтобы, глядя с конца , поворот от к был виден против хода часовой стрелки (рис. 73).

Рис. 73

9а Не заданы ни уравнения движения, ни кинематические параметры абсолютного движения МТ:

11 Используя правило параллелограмма и теорему косинусов, получим абсолютную скорость МТ:

здесь .

Проектируя абсолютное ускорение МТ (второе уравнение 3) на оси неподвижной системы координат Oxyz, получим:

12 Ответ: