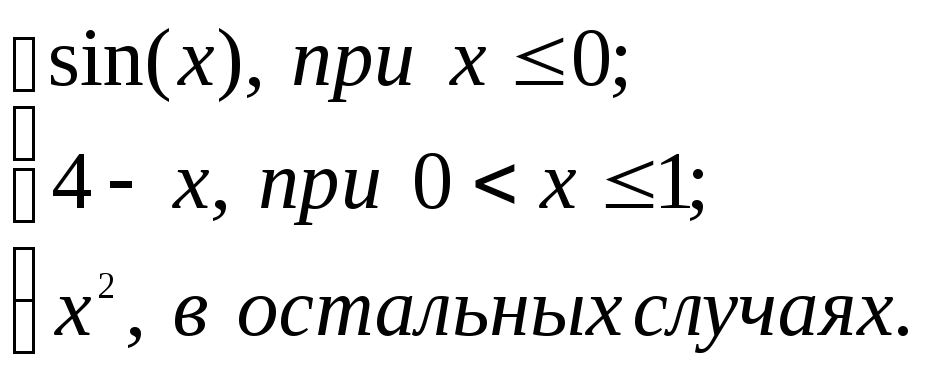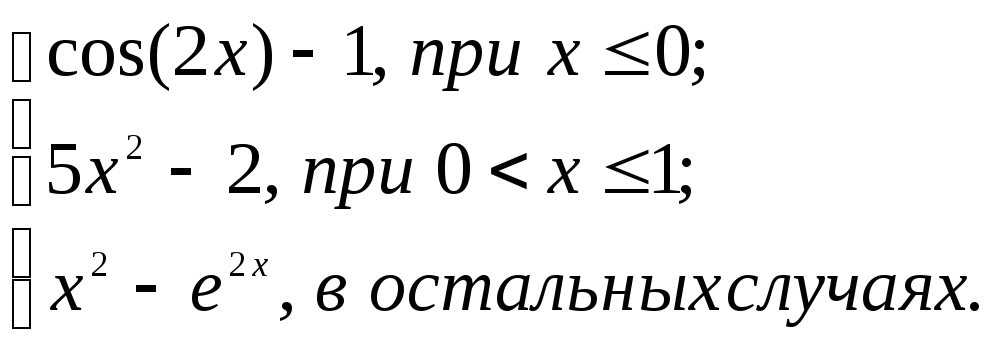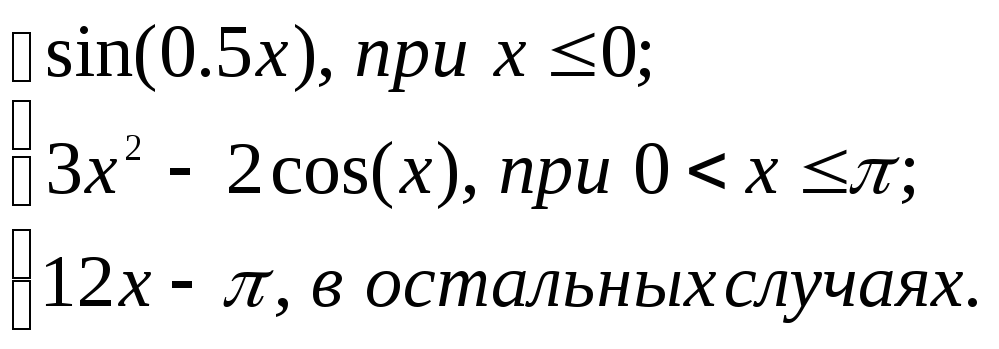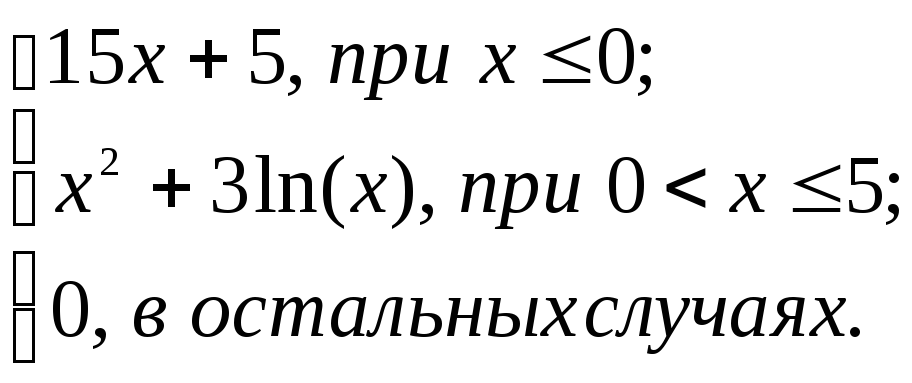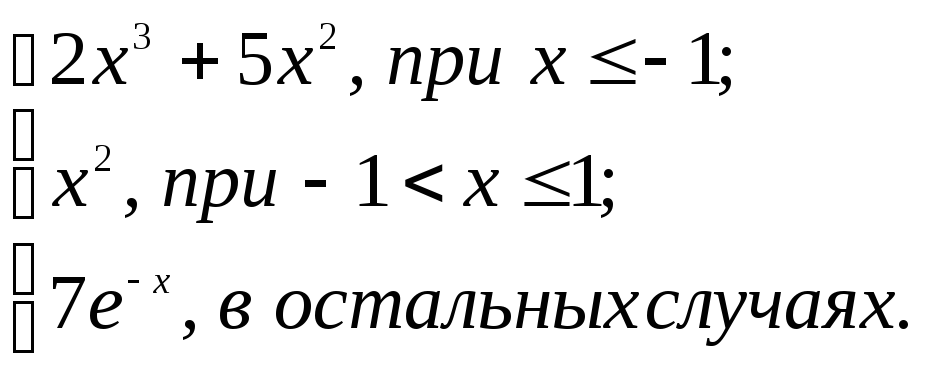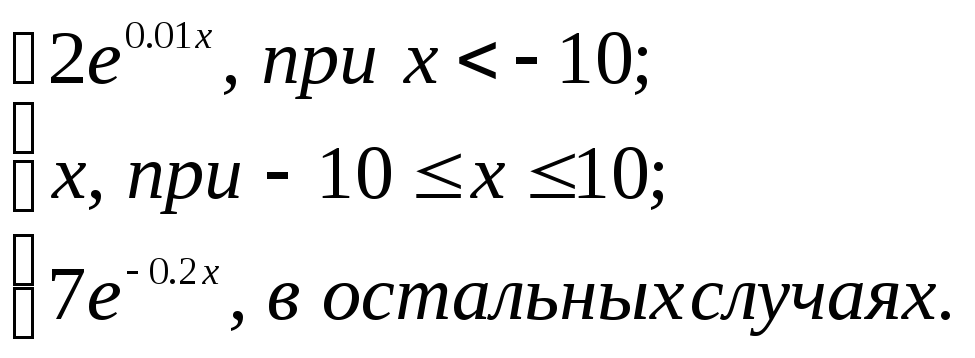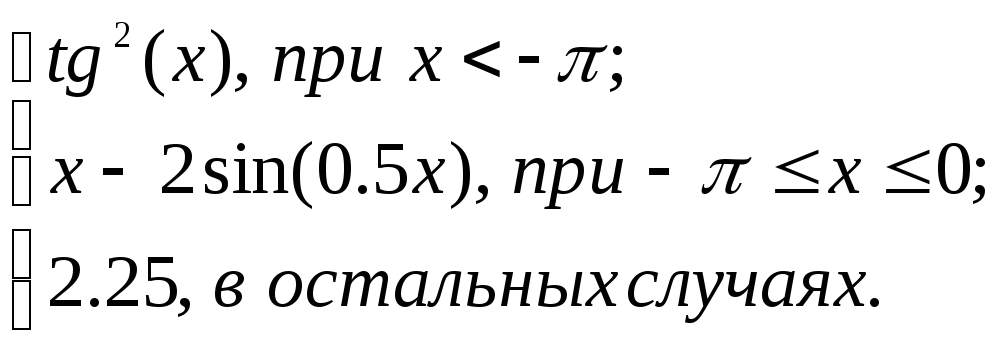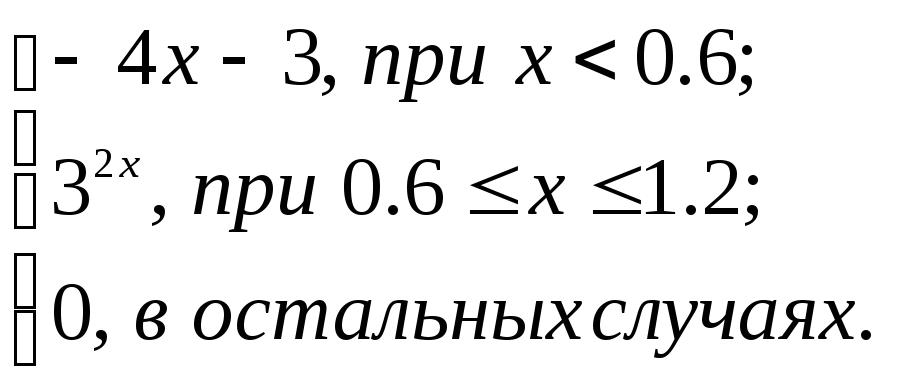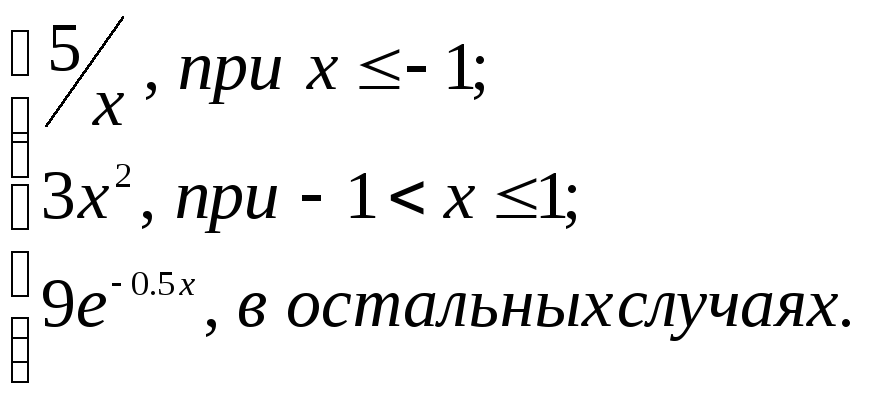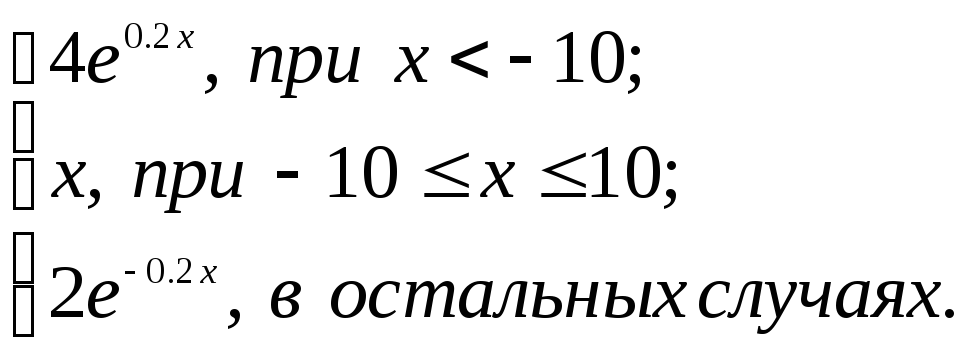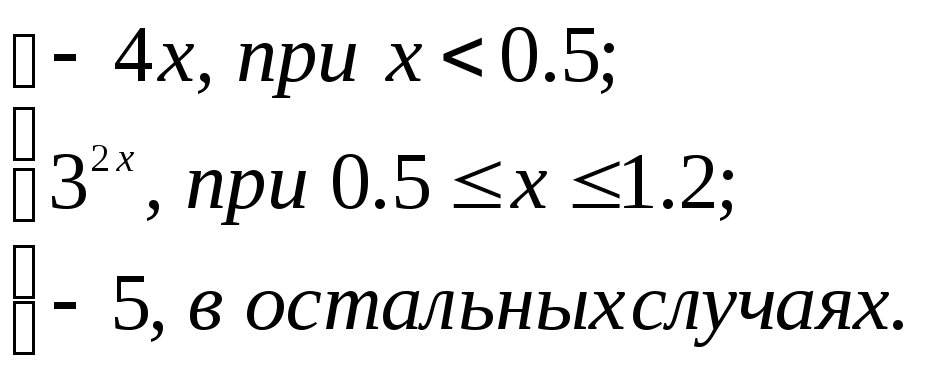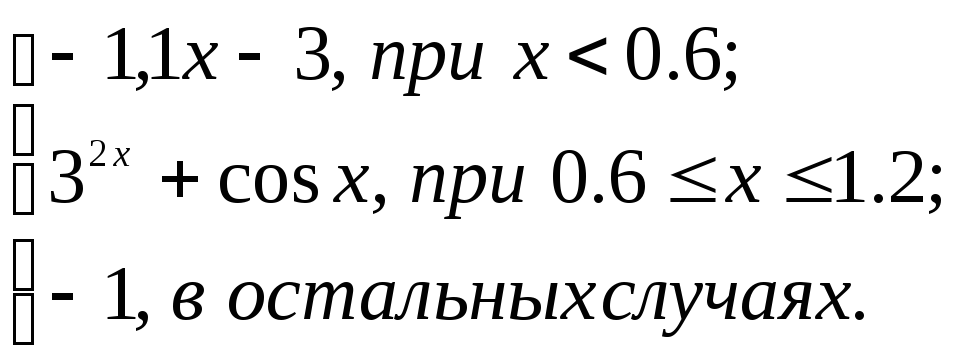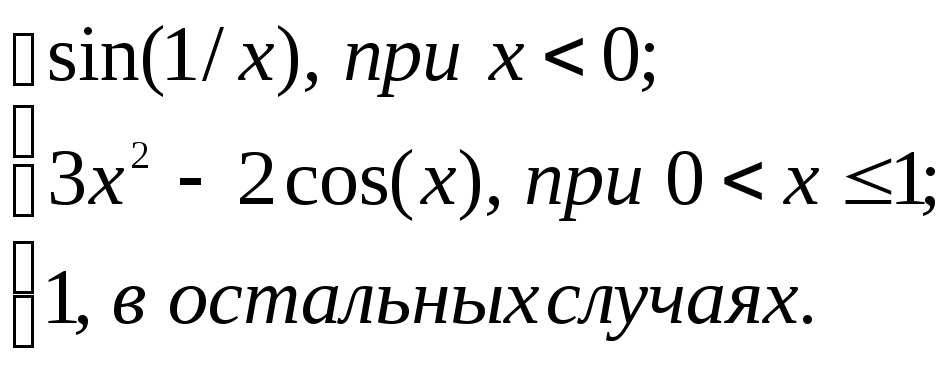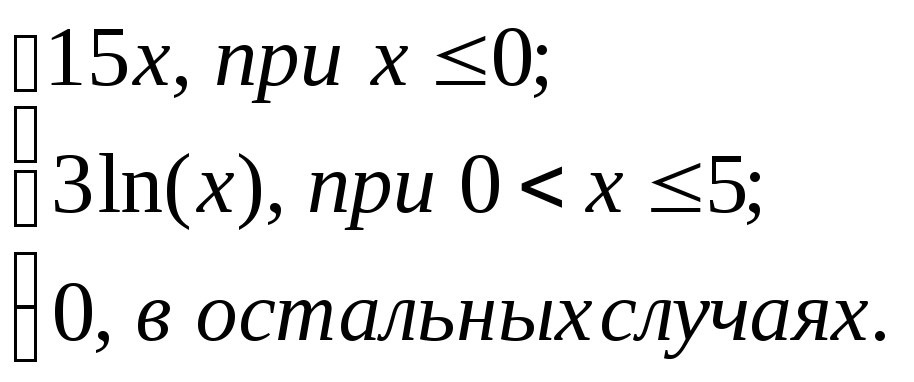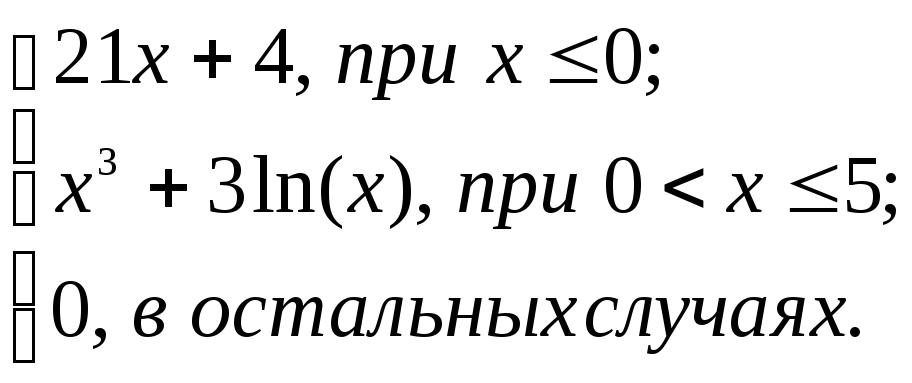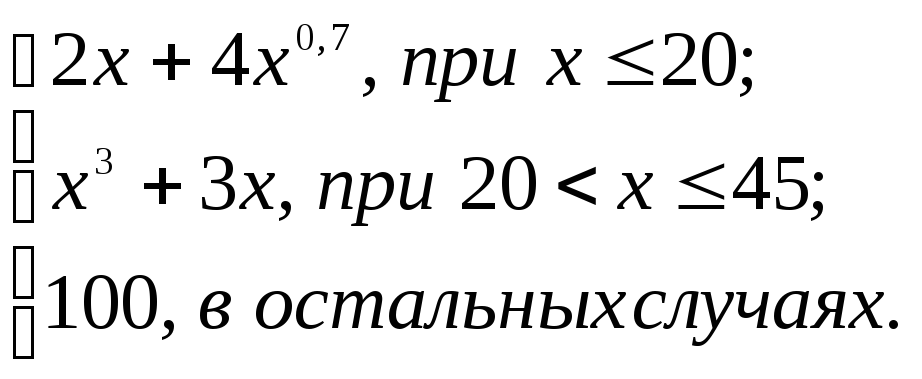- •Министерство образования и науки Российской Федерации
- •Саратовский государственный технический университет информатика. Алгоритмизация и программирование
- •Содержание
- •Введение
- •Требования к оформлению курсовой работы
- •Задания по алгоритмизации и программированию
- •2.2. Задание 2
- •3. Примеры алгоритмов и программ
- •3.1. Примеры решения задач
- •3.2. Примеры алгоритмов и программ, выполненных на алгоритмическом языке turbopascal
- •Литература
- •Информатика. Алгоритмизация и программирование
2.2. Задание 2
Вычислить функцию
![]() для
для![]() с шагомh.
Схемаалгоритма
для данной задачи – циклический процесс
вычисления по
с шагомh.
Схемаалгоритма
для данной задачи – циклический процесс
вычисления по
![]() с шагом
с шагом![]() ,
причем с использованием разветвляющего
процесса вычисления для каждого
,
причем с использованием разветвляющего
процесса вычисления для каждого![]() .
При программировании этой задачи
желательно применить все три цикла,
т.е. цикл с предусловием, цикл с постусловием
и цикл - счетчик, когда известно сколько
раз цикл должен проработать.
.
При программировании этой задачи
желательно применить все три цикла,
т.е. цикл с предусловием, цикл с постусловием
и цикл - счетчик, когда известно сколько
раз цикл должен проработать.
Номер варианта предлагается студенту из табл.2 на усмотрение преподавателя.
Таблица 2
|
Ва- ри- ан- ты |
Начало отрезка a |
Конец отрезка b |
Шаг по отрезку [a,b] h |
f(x) |
|
1 |
2 |
3 |
4 |
5 |
|
1 |
-0.5 |
0.5 |
0.01 |
|
Продолжение табл.2
|
1 |
2 |
3 |
4 |
5 | |
|
2 |
|
|
|
| |
|
3 |
|
|
|
| |
|
4 |
– 3 |
6 |
0.5 |
| |
|
5 |
– 2.1 |
3 |
0.3 |
| |
|
6 |
– 20 |
20 |
4 |
| |
|
7 |
|
|
|
| |
|
8 |
0 |
1.4 |
0.1 |
| |
|
9 |
– 12 |
0 |
1 |
| |
Окончание табл.2
|
1 |
2 |
3 |
4 |
5 |
|
10 |
– 2 |
2 |
0.25 |
|
|
11 |
-20 |
20 |
0,5 |
|
|
12 |
0 |
1.4 |
0.1 |
|
|
13 |
0 |
1.4 |
0.1 |
|
|
14 |
-2 |
2 |
0.1 |
|
|
15 |
– 3 |
7 |
0.5 |
|
|
16 |
– 3 |
6 |
0.5 |
|
|
17 |
– 9 |
9 |
1 |
|
|
18 |
0 |
120 |
2,5 |
|
ЗАДАНИЕ 3
Студенты в курсовых работах и дипломном проекте выполняют расчеты, в которых часто требуется найти корни нелинейных уравнений.
В данном разделе
предлагаются
задачи, которые можно решить, применив
методделения отрезка пополам на
интервале![]() ,
и найти с точностью
,
и найти с точностью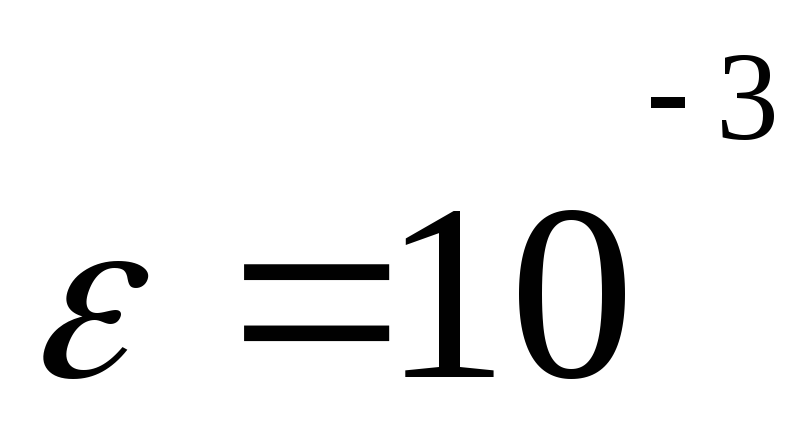 корни уравнения
корни уравнения![]() .
.
Вариант задания выдается индивидуально каждому студенту из табл.3.
Требования к выполнению задания приводятся в пункте 1 методических указаний.
Метод деления отрезка пополам - один из простейших методов нахождения корней нелинейных уравнений. Он состоит в следующем. Допустим, что удалось найти отрезок [a, b], в котором расположено искомое значение корня x = c, т.е. a<c<b.
В качестве начального приближения корня c принимаем середину этого отрезка, т.е. c=(a+b)/2. Далее исследуем значение функции f(x) на концах отрезков [a, c] и [c, b], т.е. в точках a, c, b. Тот отрезок, на концах которого f(x) принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового отрезка, внутри которого находится корень. Вторую половину отрезка [a, b], на которой знак f(x) не меняется, отбрасываем. В качестве второй итерации корня принимаем середину нового отрезка и т.д.
Итерационный процесс продолжается до тех пор, пока значение функции f(x) после n-й итерации не станет по модулю меньшим некоторого заданного значения ε, т.е. |f(c)|< ε.
Таблица 3
|
№ |
a |
b |
f(x) |
|
1 |
2 |
3 |
4 |
|
1 |
0 |
1 |
|
|
2 |
-10 |
10 |
|
Окончание табл.3
|
1 |
2 |
3 |
4 |
|
3 |
1 |
4 |
|
|
4 |
1 |
6 |
|
|
5 |
– 3 |
1 |
|
|
6 |
0 |
3 |
|
|
7 |
0,2 |
1,4 |
|
|
8 |
0 |
2 |
|
|
9 |
– 3 |
0 |
|
|
10 |
7 |
11 |
|
|
11 |
0,1 |
0,6 |
|
|
12 |
1,5 |
1,7 |
|
|
13 |
4 |
7 |
|
|
14 |
– 3 |
– 2 |
|
|
15 |
5 |
7 |
|
|
16 |
– 4 |
– 1 |
|
|
17 |
2 |
4 |
|
|
18 |
0,5 |
2 |
|
ЗАДАНИЕ 4
Вычислить
определенный интеграл
![]() любым известным методом, например,
методом прямоугольников:
любым известным методом, например,
методом прямоугольников: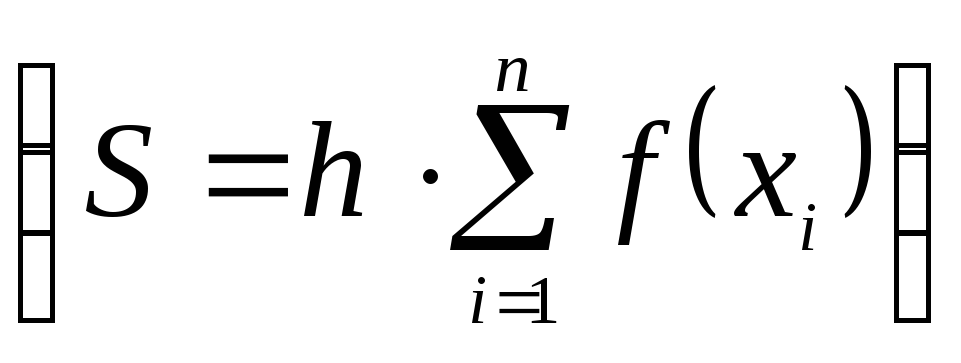 ,
или трапеций
,
или трапеций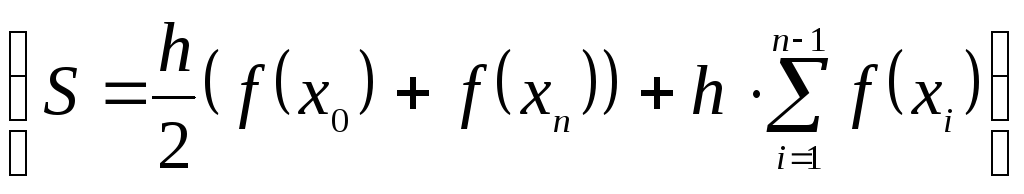 ,
или любой другой, на выбор.
,
или любой другой, на выбор.
![]() ,
,![]() ,
,![]() ,
,![]() ,
с точностью
,
с точностью
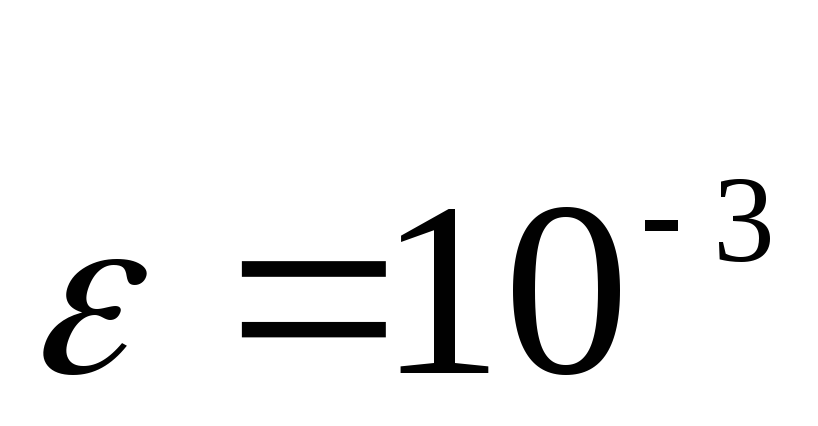 .
.
Метод прямоугольников - простейший метод численного интегрирования. Он непосредственно использует замену определённого интеграла интегральной суммой.
Отрезок [a, b] разбивается на n равных частей; h, S рассчитываются по вышеприведенным формулам. Когда модуль разности последней и предыдущей сумм становится меньше ε, вычисления завершаются, в противном случае n удваивается и вычисления повторяются.
Вариант задания выдает преподаватель индивидуально каждому студенту из табл.4.
Первоначальное n задается любое из интервала от 4 до 12. Требования к выполнению и оформлению остаются прежними.
Таблица 4
|
№ |
|
|
|
|
1 |
2 |
3 |
4 |
|
1 |
0 |
1 |
|
|
2 |
5 |
10 |
|
|
3 |
1 |
3 |
|
|
4 |
1 |
2,5 |
|
|
5 |
– 3 |
1 |
|
Окончание табл.4
|
1 |
2 |
3 |
4 |
|
6 |
0 |
3 |
|
|
7 |
– 3 |
2 |
|
|
8 |
0 |
|
|
|
9 |
|
0 |
|
|
10 |
1 |
7 |
|
|
11 |
|
|
|
|
12 |
0,5 |
3 |
|
|
13 |
– 1 |
2 |
|
|
14 |
1,85 |
3,85 |
|
|
15 |
0 |
|
|
|
16 |
– 4 |
– 1 |
|
|
17 |
|
0 |
|
|
18 |
2 |
4 |
x4-6x3+11x2+x+4 |
ЗАДАНИЕ 5
Задание выдает преподаватель каждому студенту индивидуально из ниже приведенных задач.
Задачи посвящены работе с одномерными и двумерными массивами.
Значения для n,m выбираются студентами произвольно, индекс i изменяется от 1 до n, а индекс j - соответственно от 1 до m, причем m и n могут совпадать.
Задачи:
Дана квадратная матрица Bi,j размером
 .
Найти векторai,
который составлен из наименьших членов
матрицы (по строкам) до главной диагонали
включительно. Первый элемент вектора
a1=b11.
Вывести на печать значения вектора ai.
.
Найти векторai,
который составлен из наименьших членов
матрицы (по строкам) до главной диагонали
включительно. Первый элемент вектора
a1=b11.
Вывести на печать значения вектора ai.Даны прямоугольные матрицы Ai,j и Bi,j размером
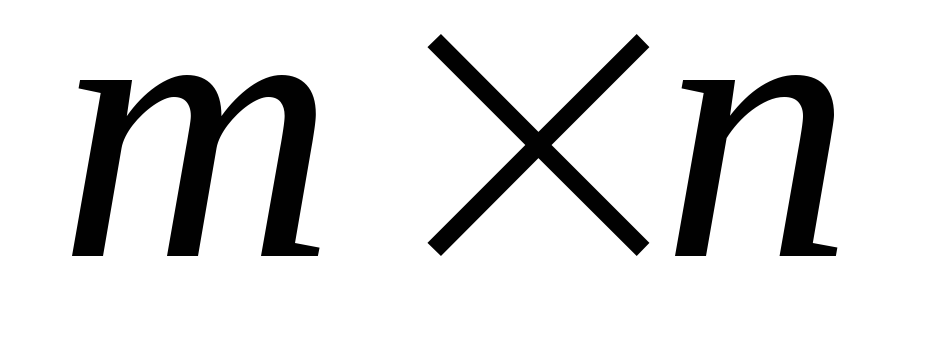 каждая. Найти матрицуCi,j,
каждый член которой равен
среднеарифметическому значению
соответствующих членов матриц Ai,j
и Bi,j.
Вывести на печать значения матрицы
Ci,j,
в виде матрицы.
каждая. Найти матрицуCi,j,
каждый член которой равен
среднеарифметическому значению
соответствующих членов матриц Ai,j
и Bi,j.
Вывести на печать значения матрицы
Ci,j,
в виде матрицы.Дана прямоугольная матрица Ai,j,, размером
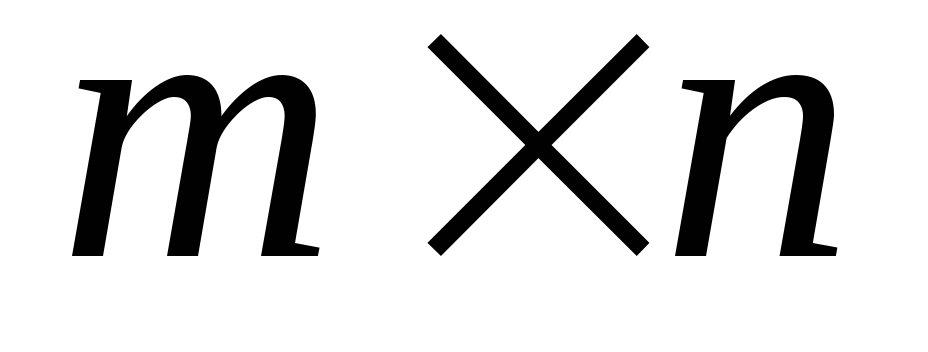 .
Расположите в прямоугольной матрицеBi,j
размером
.
Расположите в прямоугольной матрицеBi,j
размером
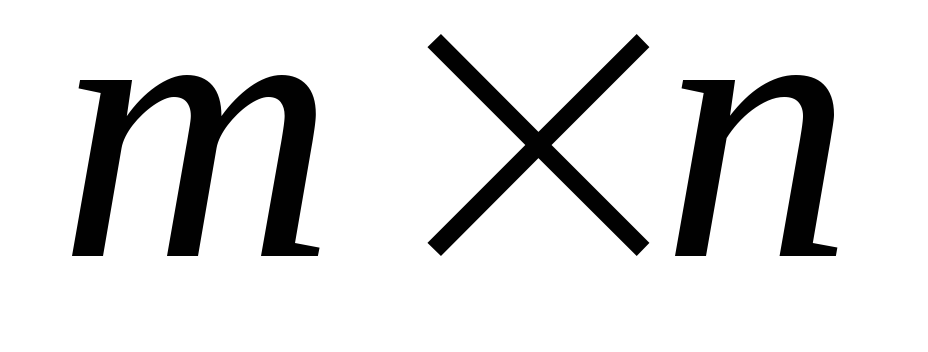 элементы матрицыAi,j
по
убыванию (по строкам). Напечатайте в
виде матрицы элементы матрицы Bi,j.
элементы матрицыAi,j
по
убыванию (по строкам). Напечатайте в
виде матрицы элементы матрицы Bi,j.Дана прямоугольная матрица Bi,j размером
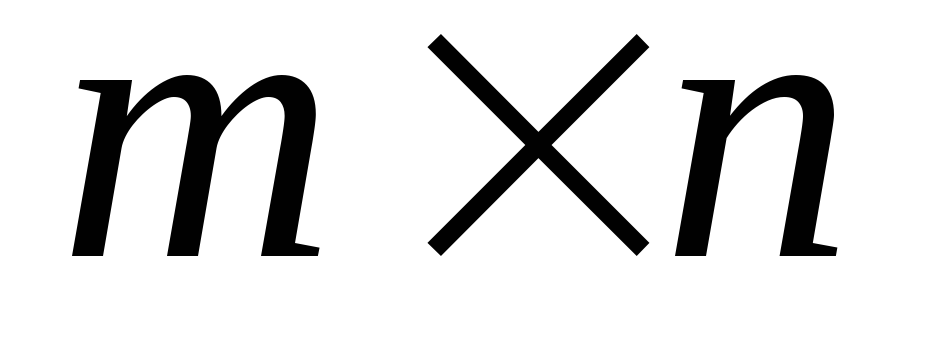 .
Найти минимальный и максимальный
элементы матрицы. Вывести на печать их
значения.
.
Найти минимальный и максимальный
элементы матрицы. Вывести на печать их
значения.Дана прямоугольная матрица Ai,j размером
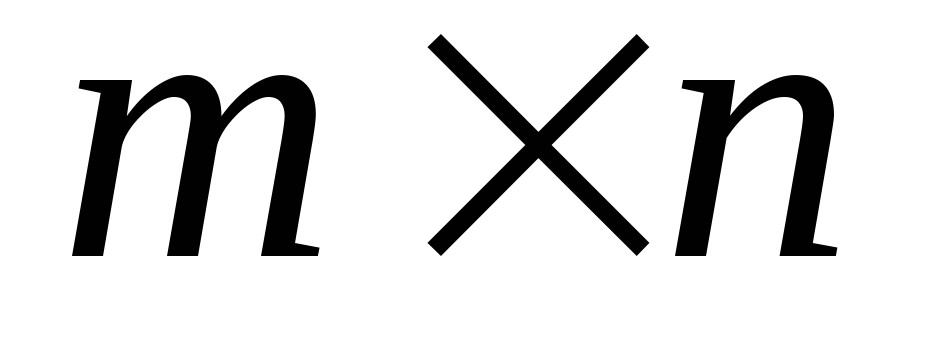 .
Определить номер строки, в которой
находится минимальный элемент матрицы,
и поменять местами эту строку и первую
строку матрицы.
Напечатать
полученную матрицу.
.
Определить номер строки, в которой
находится минимальный элемент матрицы,
и поменять местами эту строку и первую
строку матрицы.
Напечатать
полученную матрицу.Даны прямоугольные матрицы Ai,j и Bi,j размером
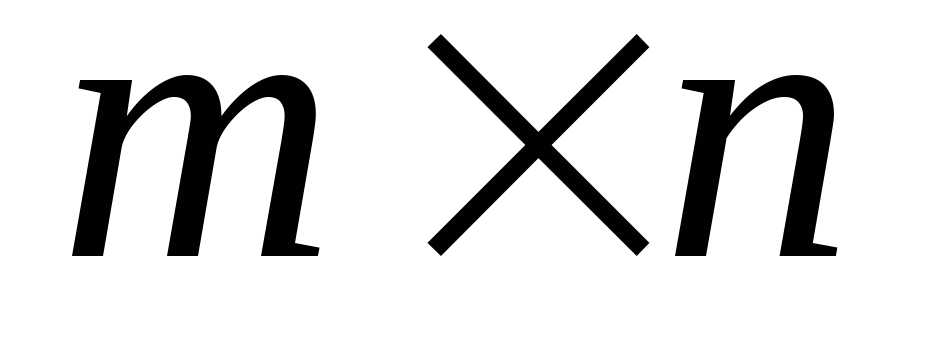 каждая. Составить программу, которая
позволяла бы находить матрицуCi,j,,
равную Ai,j
- Bi,j
или Bi,j
- Ai,j
(на выбор). Напечатать полученную
матрицу.
каждая. Составить программу, которая
позволяла бы находить матрицуCi,j,,
равную Ai,j
- Bi,j
или Bi,j
- Ai,j
(на выбор). Напечатать полученную
матрицу.Дана прямоугольная матрица Ci,j размером
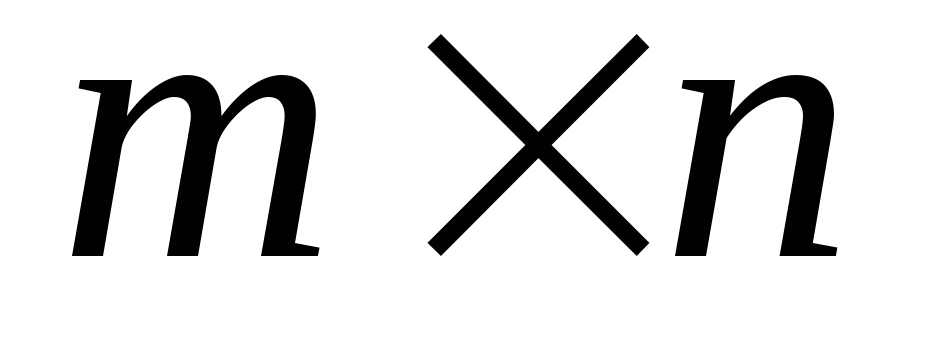 .
Определить номер строки, сумма элементов
которой максимальна. Напечатать вектор
суммы элементов матрицу по строкам.
.
Определить номер строки, сумма элементов
которой максимальна. Напечатать вектор
суммы элементов матрицу по строкам.Дана прямоугольная матрица Ci,j размером
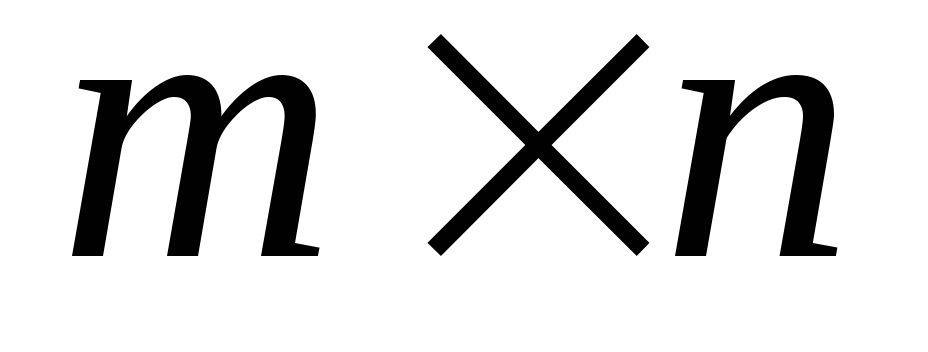 .
Найти минимальный по модулю элемент
матрицы и умножить на его значение все
элементы матрицы. Вывести полученную
матрицу на печать.
.
Найти минимальный по модулю элемент
матрицы и умножить на его значение все
элементы матрицы. Вывести полученную
матрицу на печать.Дана прямоугольная матрица Ci,j размером
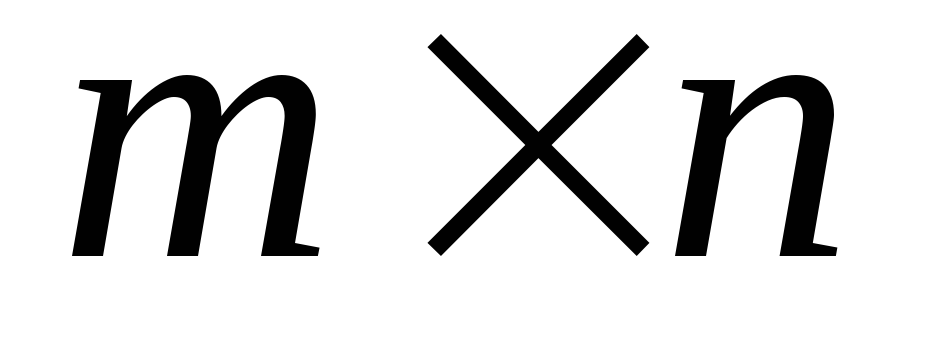 .
Если данная матрица является квадратной,
найти сумму элементов главной диагонали,
в противном случае найти сумму всех
членов матрицы. Результат напечатать.
.
Если данная матрица является квадратной,
найти сумму элементов главной диагонали,
в противном случае найти сумму всех
членов матрицы. Результат напечатать.Дана прямоугольная матрица Ci,j размером
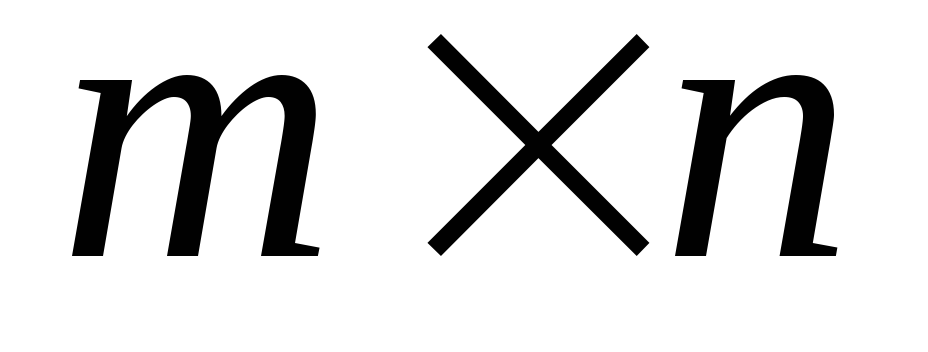 .
Найти среднеарифметическое значение
всех членов матрицы. Затем умножить на
него все значения элементов матрицы и
распечатать полученную матрицу и
среднеарифметическое значение всех
членов матрицы.
.
Найти среднеарифметическое значение
всех членов матрицы. Затем умножить на
него все значения элементов матрицы и
распечатать полученную матрицу и
среднеарифметическое значение всех
членов матрицы.Дана прямоугольная матрица Ci,j размером
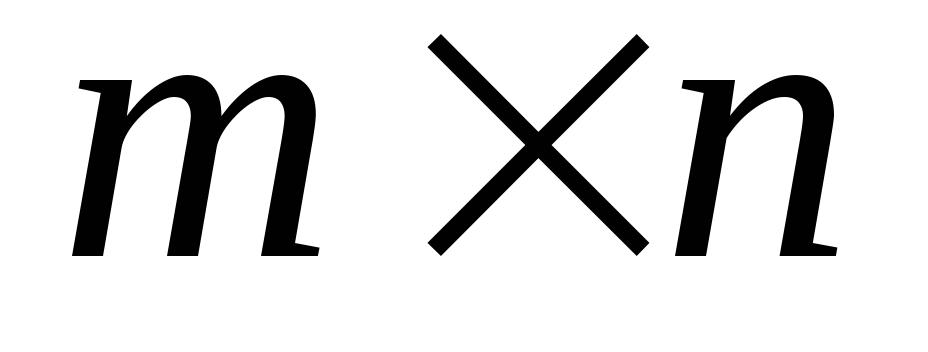 .
Найти максимальный по модулю член
матрицы и разделить все члены матрицы
на модуль данного члена. Полученную
матрицу вывести на печать.
.
Найти максимальный по модулю член
матрицы и разделить все члены матрицы
на модуль данного члена. Полученную
матрицу вывести на печать.Даны прямоугольные матрицы Ai,j размером
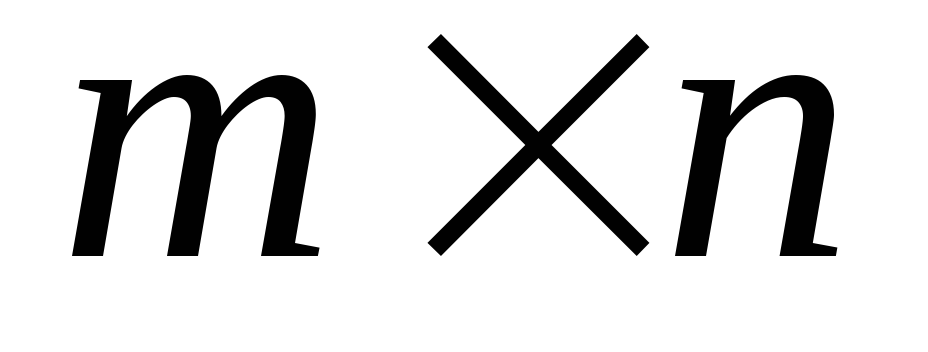 иBi,j
размером
иBi,j
размером
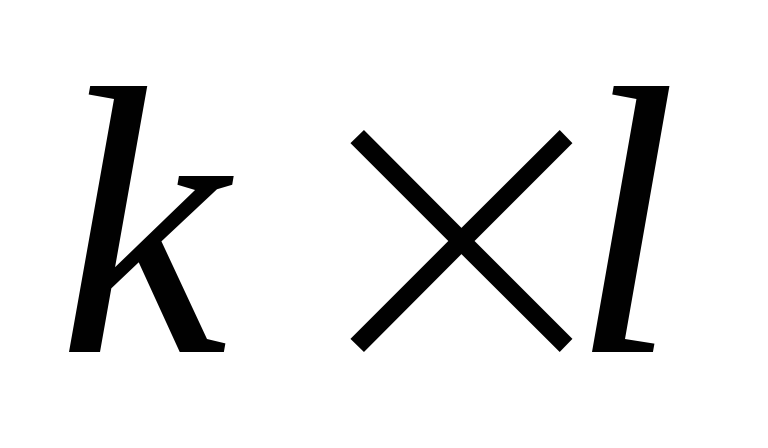 .
Найти произведение матриц, полагая,
чтоn=k.
Результат напечатать в виде матрицы.
.
Найти произведение матриц, полагая,
чтоn=k.
Результат напечатать в виде матрицы.Дана квадратная матрица Bi,j размером
 .
Найти векторai.,
который составлен из наибольших членов
матрицы (по строкам) до главной диагонали
включительно. Первый элемент вектора
a1=b11.
Вывести на печать значения вектора ai.
.
Найти векторai.,
который составлен из наибольших членов
матрицы (по строкам) до главной диагонали
включительно. Первый элемент вектора
a1=b11.
Вывести на печать значения вектора ai.Дана квадратная целочисленная матрица Ai,j размером
 .
Найти произведение членов матрицы по
тому столбцу, в котором находится
максимальное число матрицы. Результат
вывести на печать.
.
Найти произведение членов матрицы по
тому столбцу, в котором находится
максимальное число матрицы. Результат
вывести на печать.Даны прямоугольные целочисленные матрицы Ai,j и Bi,j размером
 .
Вывести на печать элементы этих матриц,
кратные трем и пяти соответственно.
.
Вывести на печать элементы этих матриц,
кратные трем и пяти соответственно.Дана прямоугольная матрица C1i,j размером
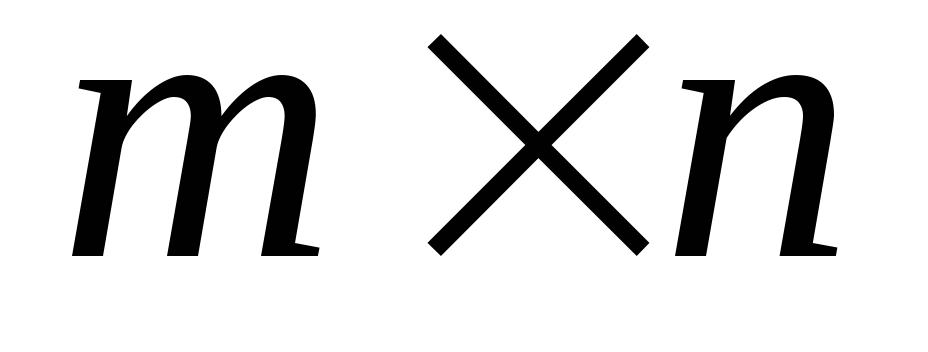 .
Расположите в вектореC2i
размером
n
элементы матрица C1i,j
, причем
сначала положительные элементы, затем
нулевые элементы и в последнюю очередь
- отрицательные.
.
Расположите в вектореC2i
размером
n
элементы матрица C1i,j
, причем
сначала положительные элементы, затем
нулевые элементы и в последнюю очередь
- отрицательные.Дана прямоугольная матрица Ci,j размером
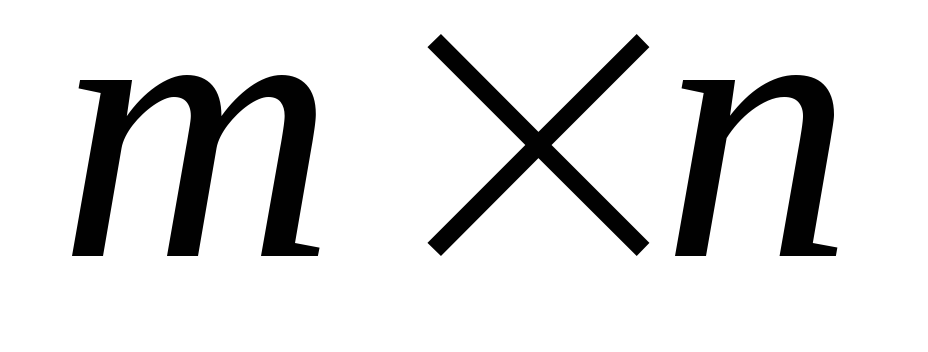 .
Найти максимальный по модулю элемент
матрицы и умножить на его значение все
элементы матрицы.
.
Найти максимальный по модулю элемент
матрицы и умножить на его значение все
элементы матрицы.Вычислить и запомнить суммы положительных элементов каждой строки прямоугольной матрицы Ci,j размером
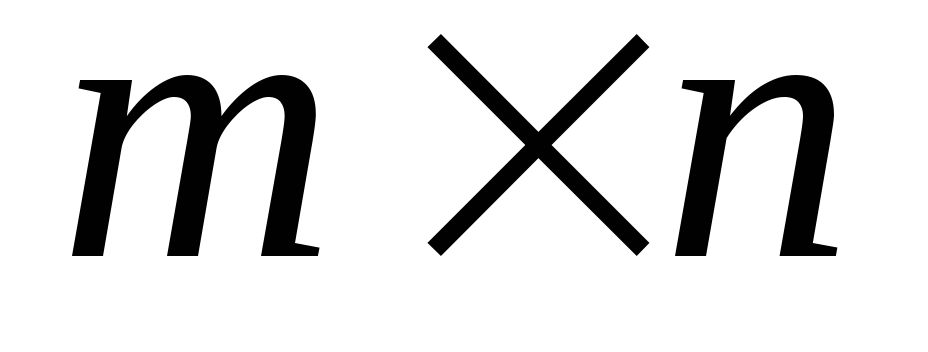 .
Результат показать в виде одномерной
матрицыSi
.
.
Результат показать в виде одномерной
матрицыSi
.