
Цель работы: экспериментальное изучение линейной цепи синусоидального тока, состоящей из последовательно соединенных активного сопротивления, индуктивной катушки и конденсатора; изучение основных закономерностей в такой цепи. Изучение резонанса напряжений.
Существуют системы элементов, которые называются гармоническими осцилляторами, отличительной особенностью которых является возможность возникновения в них гармонических (синусоидальных) колебаний с некоторой определенной частотой ω0 при наличии некоторого запаса энергии. Эта частота называется собственной частотой системы. Примерами таких систем являются груз, подвешенный на пружине, или электрический контур, содержащий емкость и индуктивность.
![]()
![]()
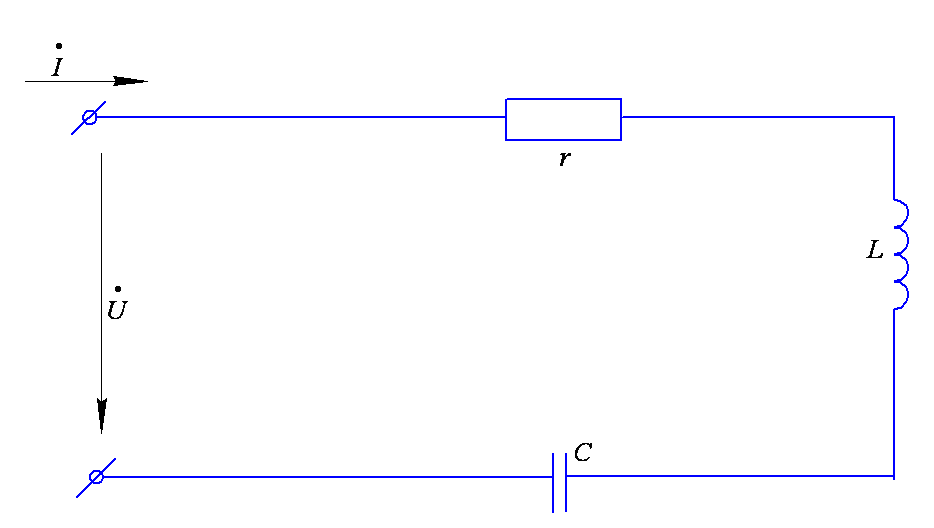

Рис.1 Рис.2
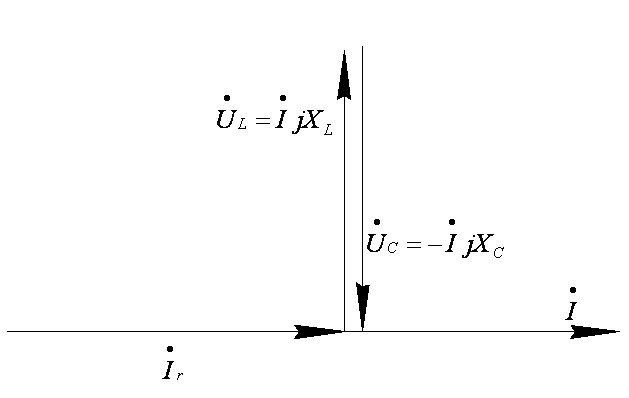
Рис.3
Рассмотрим цепь, содержащую последовательно соединенные индуктивность, емкость и активное сопротивление (рис. 1). Для этой цепи закон Ома:
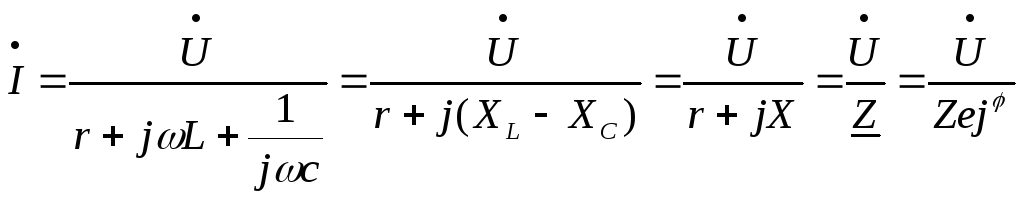
или для действующих значений:
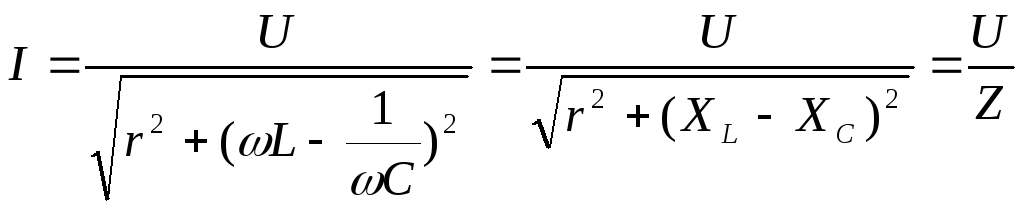
В общем случае ток и напряжение в такой цепи не совпадает по фазе. Этот видно из векторной диаграммы (рис. 2).
Угол сдвига фаз
![]() между током
между током
![]() и напряжением
и напряжением
![]() :
:
![]()
Резонанс напряжений - это явление, наступающее в электрической цепи синусоидального тока, содержащей последовательно соединенные активное сопротивление, индуктивную катушку и конденсатор, и заключающееся в том, что ток в цепи и приложенное ко всей цепи напряжение совпадают по фазе.
Резонанс возникает при равенстве реактивных сопротивлений конденсатора и катушки индуктивности:
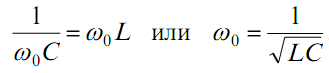
При этом условии напряжения на C и L могут существенно превышать входное напряжение.
Роль трения играет активное сопротивление r, причем при его увеличении добротность снижается. Сопротивление такой цепи в комплексной форме запишется в виде:
![]()
Условие
резонанса можно добиться, изменяя С, L,
![]() .
.
В данной работе мы рассматриваем
резонанс, возникающий в ходе изменения
![]() .
.
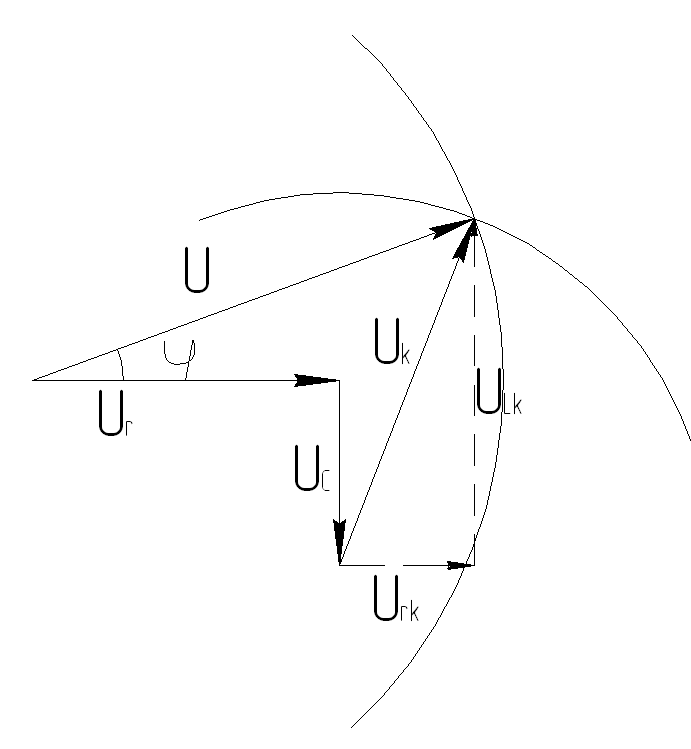
Векторная диаграмма для случая резонанса дана на рис.3. Из нее мы имеем,
![]()
где![]() - резонансные значения соответствующих
величин.
- резонансные значения соответствующих
величин.
Зависимости тока и напряжения на отдельных элементах от частоты – это резонансные кривые (рис.4)
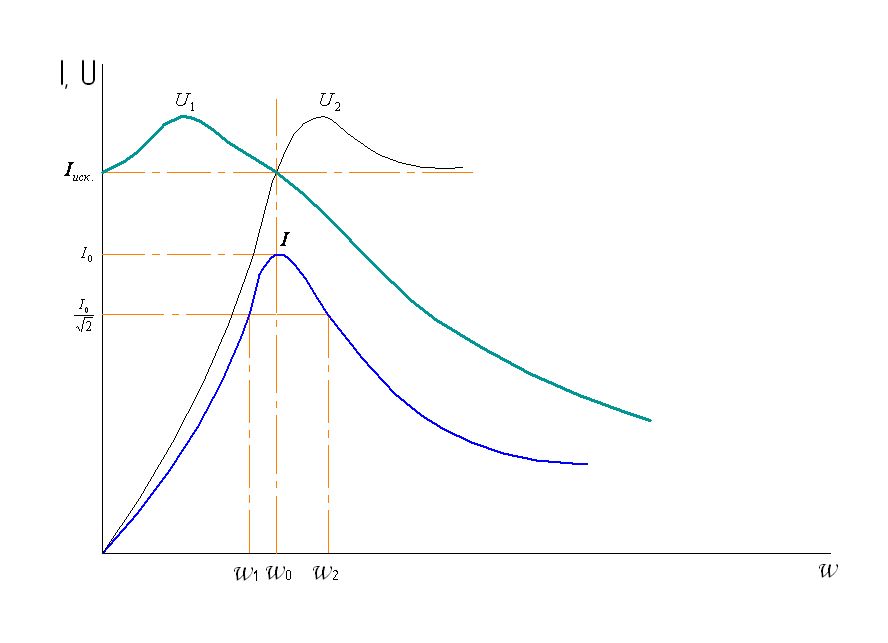 Рис.4
Рис.4
Полосу частот вблизи резонанса, на
границе которой ток снижается в
![]() раз по сравнению с резонансным значением,
называют полосой пропускания резонансного
контура.
раз по сравнению с резонансным значением,
называют полосой пропускания резонансного
контура.
При
резонансе ток в цепи I=E/R
имеет
максимальное значение.
Соотношение
![]() - называется добротностью контура.
Эта
величина показывает, во сколько раз
напряжение на реактивных сопротивлениях
превышает входное напряжение в режиме
резонанса.
- называется добротностью контура.
Эта
величина показывает, во сколько раз
напряжение на реактивных сопротивлениях
превышает входное напряжение в режиме
резонанса.
Если
частота входного напряжения
![]() <
<
![]() ,,
то
сопротивление конденсатора превышает
сопротивление катушки индуктивности,
а при
,,
то
сопротивление конденсатора превышает
сопротивление катушки индуктивности,
а при
![]() >
>
![]() ,
наоборот,
сопротивление катушки превышает
сопротивление конденсатора. В первом
случае режим называется активно-емкостным,
а во втором - активно-индуктивным.
,
наоборот,
сопротивление катушки превышает
сопротивление конденсатора. В первом
случае режим называется активно-емкостным,
а во втором - активно-индуктивным.

Рис.5
Добротность контура также можно
определить при помощи характеристики
![]() формуле:
формуле:
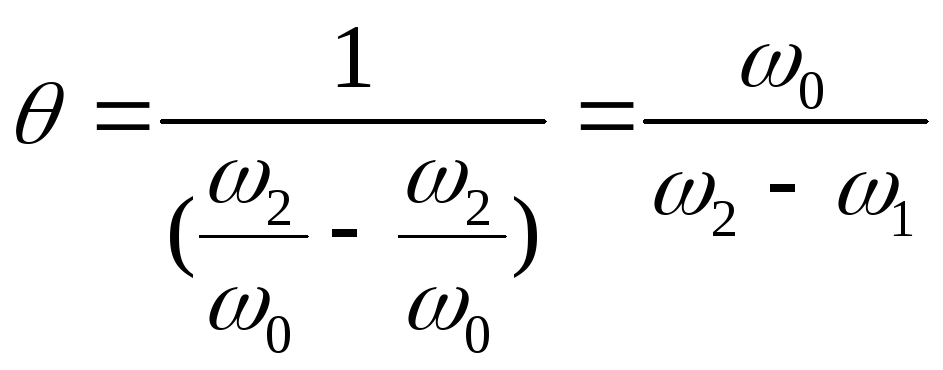
где
![]() - резонансная частота;
- резонансная частота;
![]() и
и
![]() - значения частоты, соответствующие
двум равным токам
- значения частоты, соответствующие
двум равным токам
![]() при разных знаках угла сдвига фаз
при разных знаках угла сдвига фаз
![]() .
.
Формулы и пояснения к ним необходимые для расчета данной лабораторной работы.
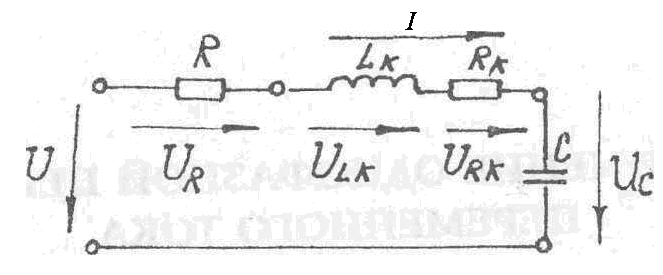
Рис.6
На рис.6 обозначены:
![]() -
действующее значение напряжения,
приложенного ко всей цепи;
-
действующее значение напряжения,
приложенного ко всей цепи;
![]() -
действующие значения напряжения на
активном сопротивлении R
индуктивной
катушке и конденсаторе соответственно;
-
действующие значения напряжения на
активном сопротивлении R
индуктивной
катушке и конденсаторе соответственно;
![]() -
действующие
значения напряжения на индуктивном
элементе
-
действующие
значения напряжения на индуктивном
элементе
![]() и резистивном элементе
и резистивном элементе
![]() соответственно;
соответственно;
![]() -
действующее значение тока в цепи.
-
действующее значение тока в цепи.
Если
![]() ,
,
где
![]() -
мгновенные значения напряжения,
приложенного к цепи, и тока, протекающего
в цепи;
-
мгновенные значения напряжения,
приложенного к цепи, и тока, протекающего
в цепи;
![]() -
их соответствующие амплитудные значения;
-
их соответствующие амплитудные значения;
![]() -
угловая частота,
-
угловая частота,
![]()
![]() -
частота тока в цепи и напряжения,
приложенного к цепи;
-
частота тока в цепи и напряжения,
приложенного к цепи;
![]() -
начальные
фазы напряжения и тока соответственно.
-
начальные
фазы напряжения и тока соответственно.
Для цепи, схема которой приведена на рис.6, выполняется закон Ома:
- для амплитудных значений тока и напряжения
![]() ,
где
,
где
![]()
- для действующих значений
![]()
Для участков цепи для действующих значений напряжения и тока закон Ома запишется в виде:
![]() ,где
,где
![]()
Угол
сдвига по фазе между током I и напряжением
![]() на индуктивной катушке определяется
как
на индуктивной катушке определяется
как
![]() .
.
Углы
сдвига по фазе между током I и напряжениями
![]() и
и
![]() на активных сопротивлениях
на активных сопротивлениях
![]() и
и
![]() соответственно
равны нулю.
соответственно
равны нулю.
Угол
сдвига по фазе между напряжением
![]() на конденсаторе и током I равен -
на конденсаторе и током I равен -
![]() (ток опережает напряжение).
(ток опережает напряжение).
Угол
сдвига
по
фазе
между
напряжением
![]() на
индуктивном
элементе
на
индуктивном
элементе
![]() и
током
I
равен
и
током
I
равен
![]() (ток
отстает
от
напряжения).
(ток
отстает
от
напряжения).
Для рассматриваемой цепи справедлив 2-й закон Кирхгофа, записанный в векторной форме:
![]()
В соответствии с этим уравнением могут быть построены векторные диаграммы для трех случаев (рис.7):
а)![]()
б)
![]()
в)
![]()
Векторная диаграмма для данной цепи
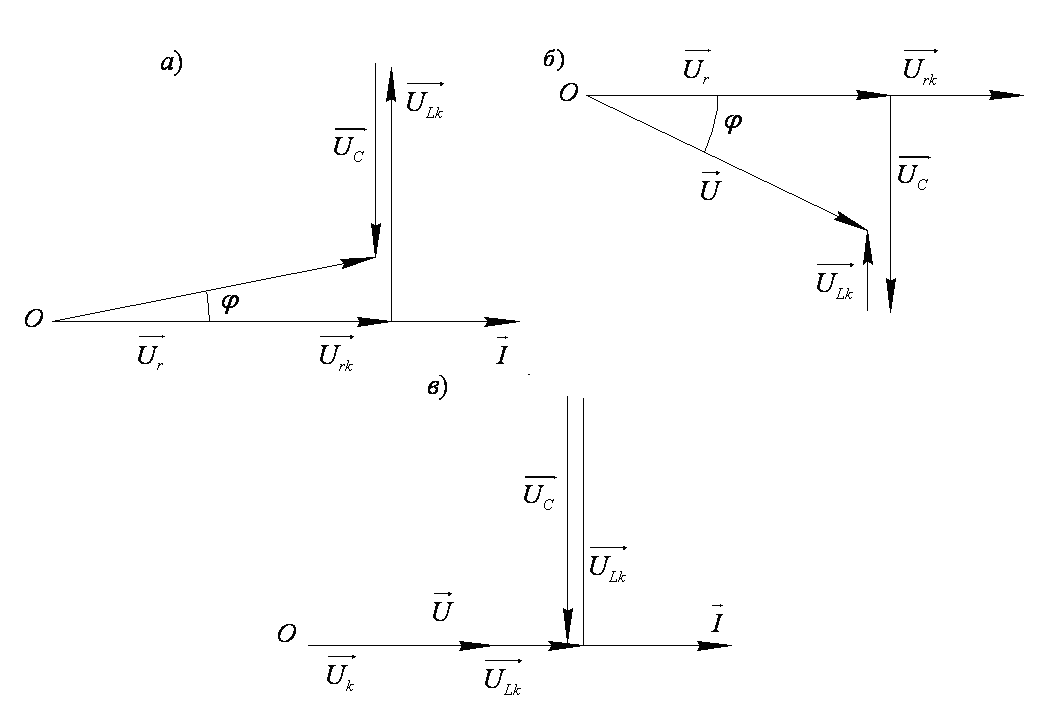
Рис.7
Для цепи рис.7 справедливы следующие соотношения для мощностей:
![]() -
активная
мощность;
-
активная
мощность;
![]() -
коэффициент
мощности;
-
коэффициент
мощности;
![]() -
реактивные
индуктивная
и
емкостная
мощности;
-
реактивные
индуктивная
и
емкостная
мощности;
![]() -
реактивная
мощность
цепи;
-
реактивная
мощность
цепи;
![]() -
полная мощность.
-
полная мощность.
Единицы измерения в системе «СИ» для величин:
Р
– Вт;
![]() - вар; S
– ВА.
- вар; S
– ВА.
При резонансе выполняются следующие основные соотношения:
-
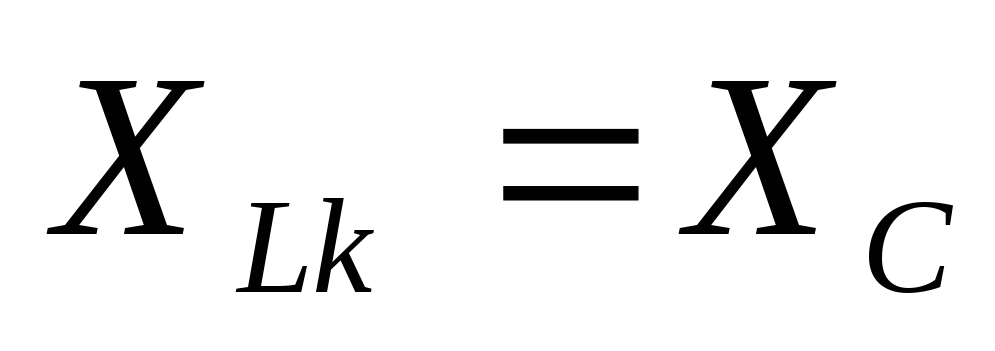 -
условие
возникновения резонанса в цепи;
-
условие
возникновения резонанса в цепи; -
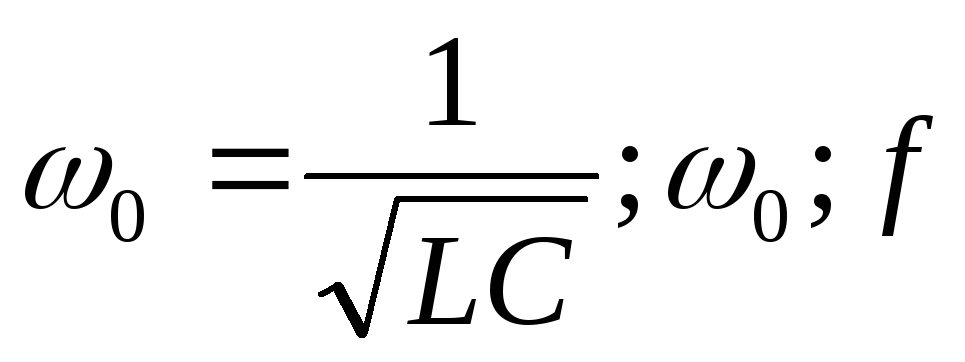 -
угловая частота, и соответствующая
ей частота синусоидального тока и
напряжения в цепи для случая резонанса;
-
угловая частота, и соответствующая
ей частота синусоидального тока и
напряжения в цепи для случая резонанса; -
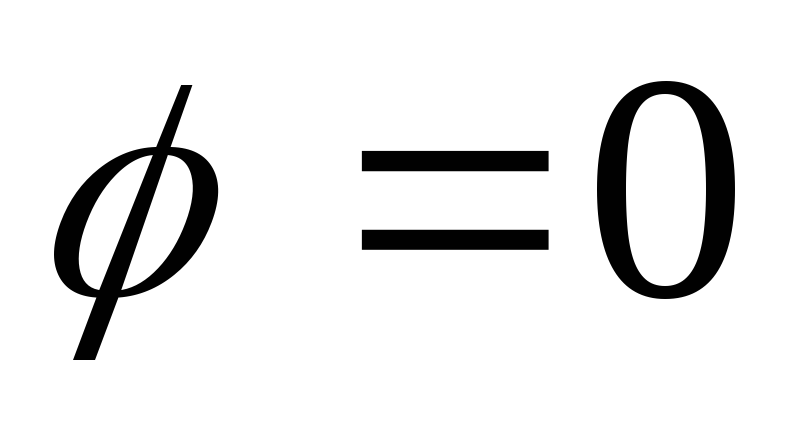
-
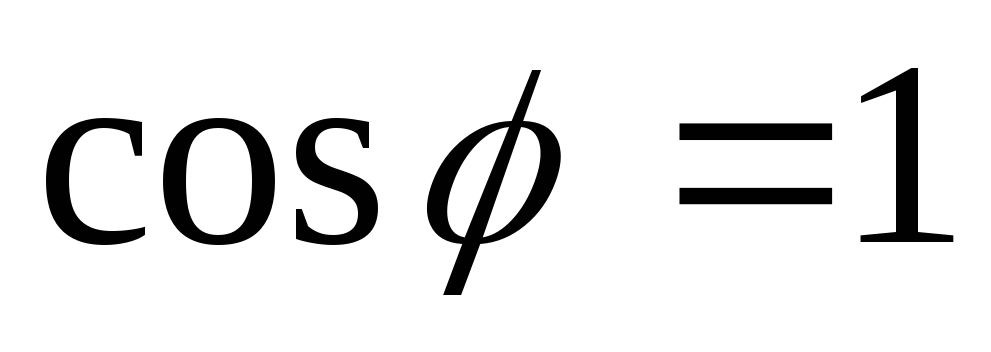
-
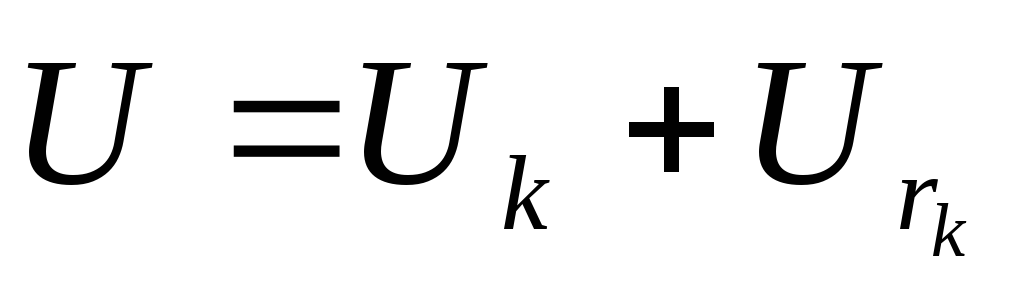
-
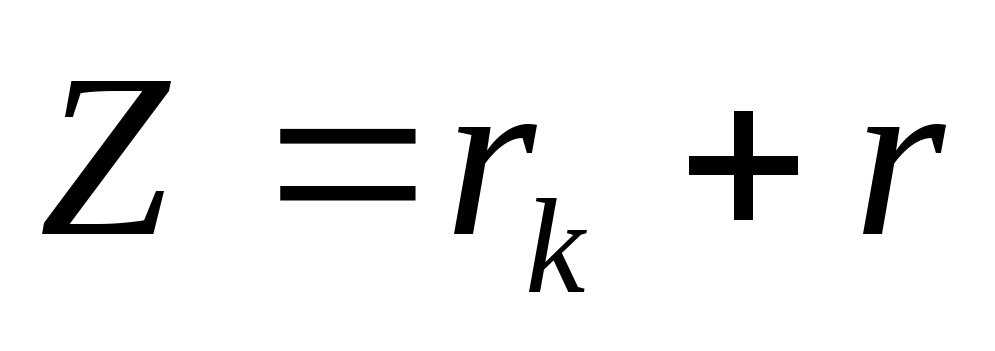
-
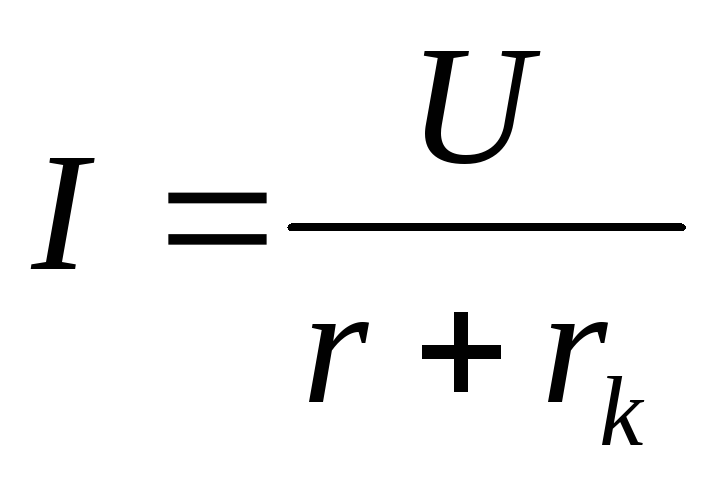
-
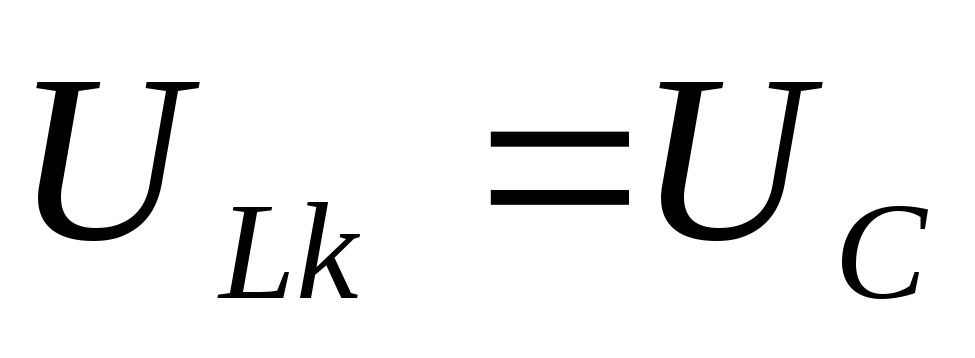
-
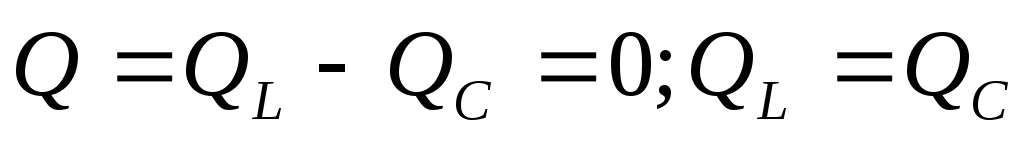
-

Отметим, что ток в цепи при резонансе напряжений максимален, напряжения на индуктивном и емкостном элементах противофазны. Векторная диаграмма, соответствующая резонансу напряжений, приведена на рис.7,в.
Порядок выполнения работы.
Работа выполняется на универсальном лабораторном стенде «Первая часть ТОЭ» (рис.8).

СД 1 Л 1 А1-А4 VI П 1 Т 1
Рис.8
Питание стенда включается тумблером Т1 (верхнее положение).
Выбор конкретной лабораторной работы осуществляется переключателем Ш (в нашем случае поставить в положение 2). Схема, исследуемая в данной лабораторной работе Л2 - «Резонанс напряжений и токов». О правильности выбора работы сигнализирует светодиод СД2.
На рис.9 показана крупным планом схема данной лабораторной работы.

Требуется:
1. Произвести подготовку установки к выполнению опыта. Для этого:
а) ознакомиться с лабораторной установкой (стендом).
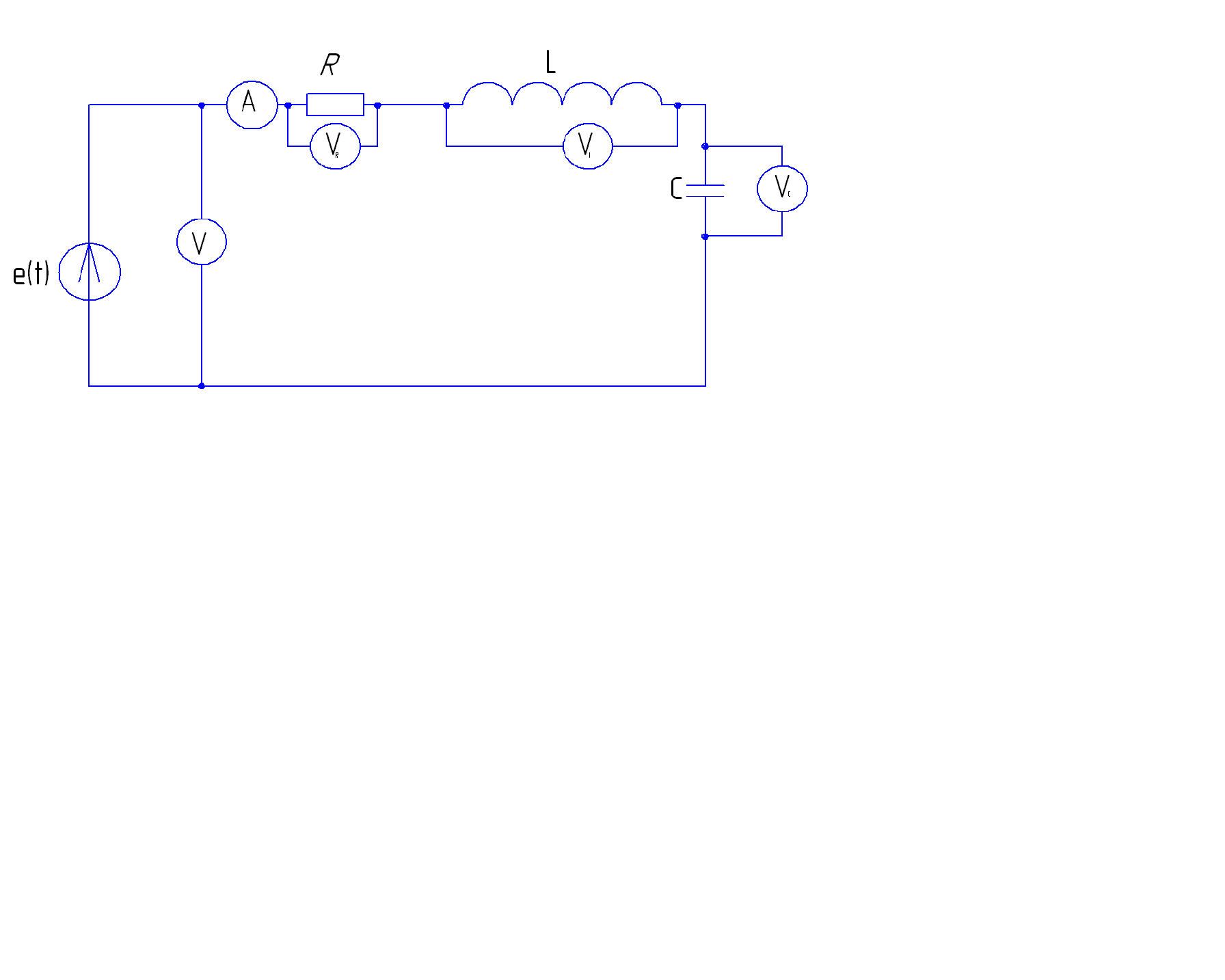
а)
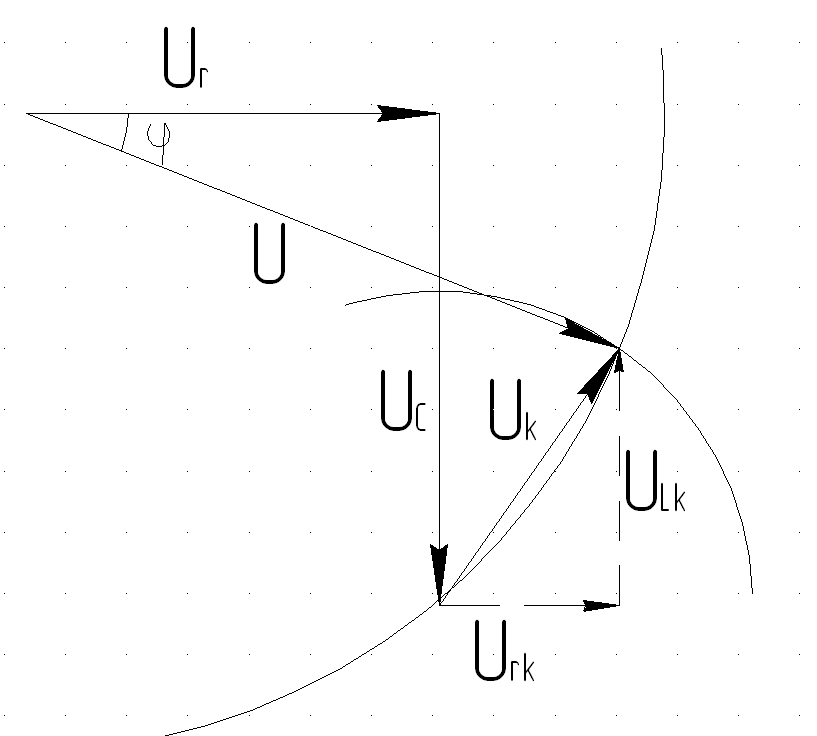
б)
ИЗУЧИТЬ В СООТВЕТСТВИИ СО СХЕМОЙ РАСПОЛОЖЕНИЕ НА ПАНЕЛЯХ СТЕНДА КАЖДОГО ИЗ ЭЛЕМЕНТОВ СХЕМЫ;
Б) РУЧКУ УПРАВЛЕНИЯ АВТОТРАНСФОРМАТОРА УСТАНОВИТЬ В КРАЙНЕЕ ЛЕВОЕ ПОЛОЖЕНИЕ;
В) СОБРАТЬ ЭЛЕКТРИЧЕСКУЮ ЦЕПЬ В СООТВЕТСТВИИ СО СХЕМОЙ;
ВНИМАНИЕ! ПРАВИЛЬНОСТЬ ВЫПОЛНЕННЫХ СОЕДИНЕНИЙ ОБЯЗАТЕЛЬНО ДО ВКЛЮЧЕНИЯ ИСТОЧНИКОВ ПИТАНИЯ ЦЕПИ ДОЛЖНА БЫТЬ ПРОВЕРЕНА ПРЕПОДАВАТЕЛЕМ ИЛИ ЛАБОРАНТОМ.
Г) УСТАНОВИТЬ ВЕЛИЧИНУ СОПРОТИВЛЕНИЯ R (С ПОМОЩЬЮ ГРАДУИРОВАННОГО ЛИМБА) В СООТВЕТСТВИИ С УКАЗАНИЯМИ ПРЕПОДАВАТЕЛЯ.
д) Изменяя частоту генератора, измерить следующие величины: ток, напряжение на конденсаторе UC, напряжение на катушке ULR, напряжение на резисторе UR. Всего провести не менее 10 групп измерений. Результаты занести в таблицу.
