Прямая линия на плоскости
.docЛекция №10
Прямая линия на плоскости
Прямая линия на плоскости может быть задана:
-
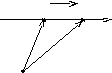
Векторным уравнением в параметрической форме.
,
,
(1)
где
- направляющий вектор прямой,
- радиус-вектор фиксированной точки
на прямой.
0
,
точка
- текущая точка прямой
.
-
Нормальным векторным уравнением
,
,
(2)
где
- нормальный вектор прямой.
0
-
Уравнение прямой, проходящей через две различные точки, может быть записано в векторной форме.
.
(3)
0
- параметр,
R.
Когда
пробегает от
до
,
тогда точка М пробегает всю прямую
.
-
Общее уравнение прямой на плоскости. Уравнение вида
(4)
называется общим уравнением прямой.
-
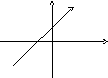
Уравнение
(5)
называется уравнением прямой с угловым коэффициентом.
y
b α
x
0
=tgα
– угловой коэффициент.
-
Уравнение прямой, проходящей через данную точку в данном направлении.
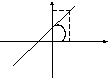y
α
0
x
,
(6)
=tgα.
-
Уравнение прямой, проходящей через две данные точки.
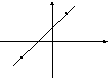y
x
0
.
(7)
-
Уравнение прямой в отрезках на осях.
. (8)
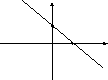y
x
0
-
Нормальное уравнение прямой линии на плоскости. Расстояние от точки до прямой на плоскости.
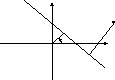y
p α x
0 d
Нормаль к прямой
образует угол α
с положительным направлением оси
.
. (9)
Расстояние от точки до прямой на плоскости находится по формуле:
.
(10)
Для нормального уравнения (9) характерно, что
.
Чтобы привести
общее уравнение прямой к нормальному
виду надо обе части этого уравнения
умножить на нормирующий множитель
:
. (11)
Знак нормирующего множителя выбирается противоположным знаку свободного члена С в общем уравнении прямой.
-
Параметрические уравнения прямой на плоскости.
–
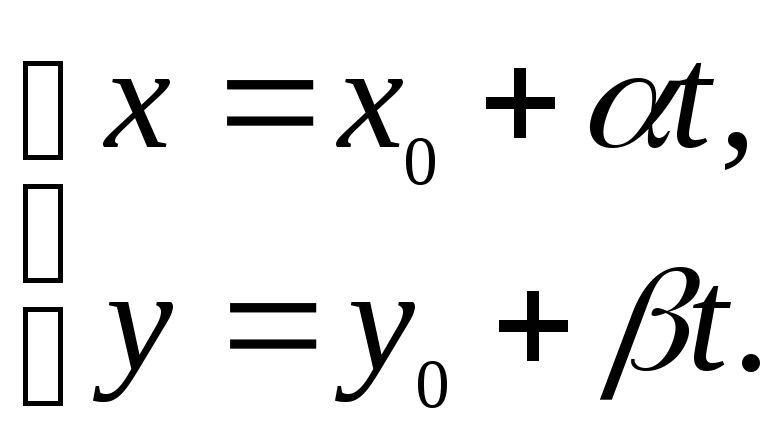
параметр,
.
Пусть две прямые заданы уравнениями:
y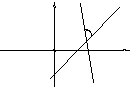
(2) (1)
0
x
Тангенс угла между этими прямыми находится по формуле
. (12)
Признаком параллельности двух прямых является равенство их угловых коэффициентов
. (13)
Признаком перпендикулярности двух прямых является соотношение
(14)
или
.
Угловые коэффициенты взаимно перпендикулярных прямых обратны по величине и противоположны по знаку.
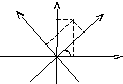
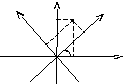
Преобразование координат точки
М
α 
0
Формулы
(15)
определяют
преобразование координат точки при
параллельном сдвиге системы осей на
величину
в направлении
,
на величину
в направлении
и последующим повороте системы на угол
.
Рисунок изображен для случая, когда
a=b=0.
Задача №1. Составить уравнения прямых на плоскости, равноудаленных от данных точек: A(3;-1), B(9;1), и C(-5;5).
y
C
L
M
B x
0 N
A
Решение.
Если бы три точки A,B,C лежали по одну сторону от искомой прямой, то они бы лежали на одной прямой, параллельной искомой. Но точки A,B,C не лежат на одной прямой – значит две из них лежат по одну сторону от искомой прямой, а третья по другую.
Если A и B лежат по одну сторону от прямой, С – по другую, то искомая прямая проходит через точки L(2;3) и M(-1;2) – середины отрезков ВС и АС соответственно. Её уравнение
или
.
Аналогично разбираются два других случая расположения точек А, В и С относительно прямой. Задача имеет три решения.
Ответ:
,
,
.
Задачи для самостоятельного решения
-
Даны вершины треугольника А(8;4), В(-12;-6), С(-4;-12). Составить следующие уравнения:
а) трех его сторон;
б) медианы, проведенной из вершины В;
в) биссектрисы угла С;
г) высоты, опущенной из вершины А на сторону ВС.
-
Начало координат перенесено в точку
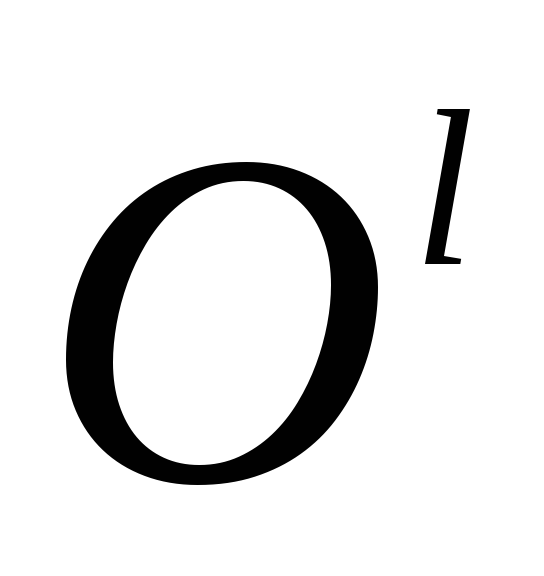с координатами (-1;2), оси координат
повернуты на угол
,
равный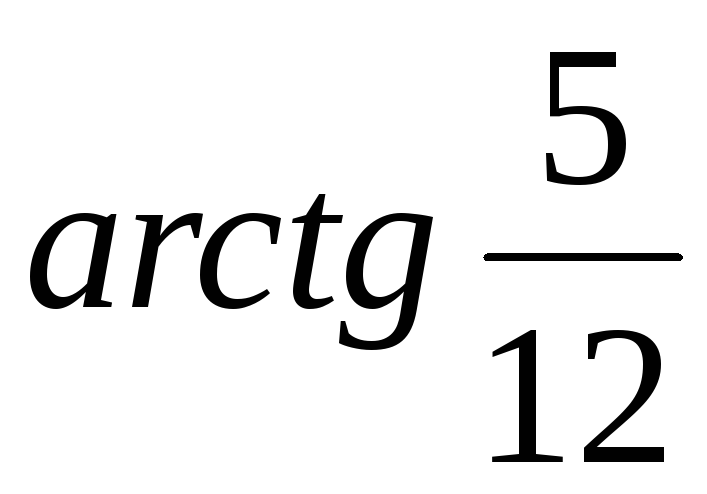
.
Координаты точек
,
,
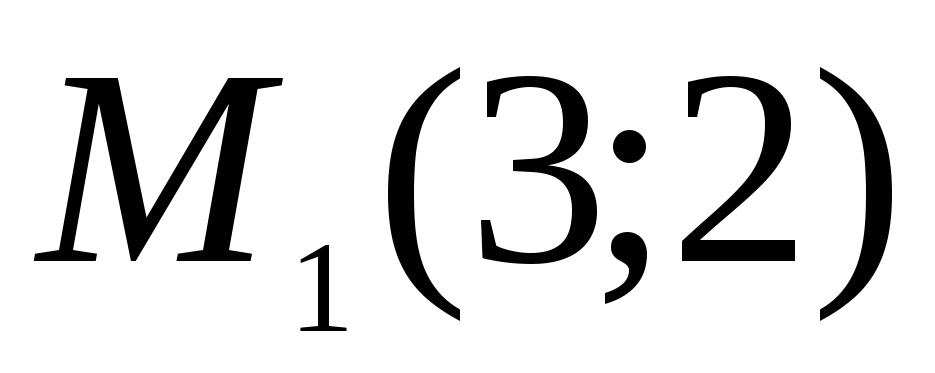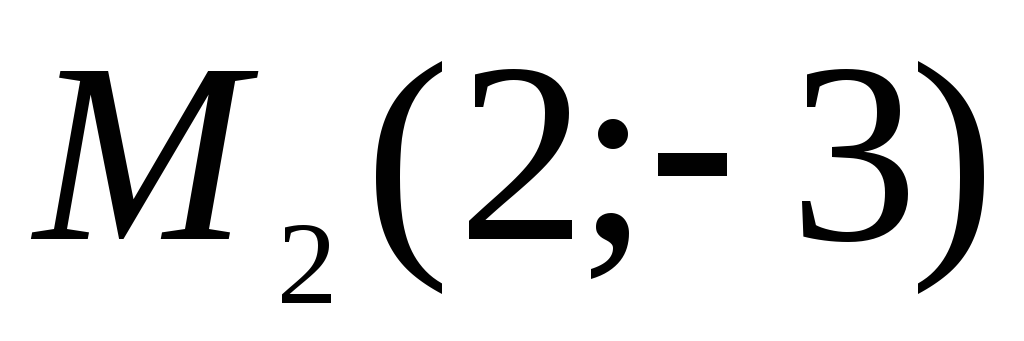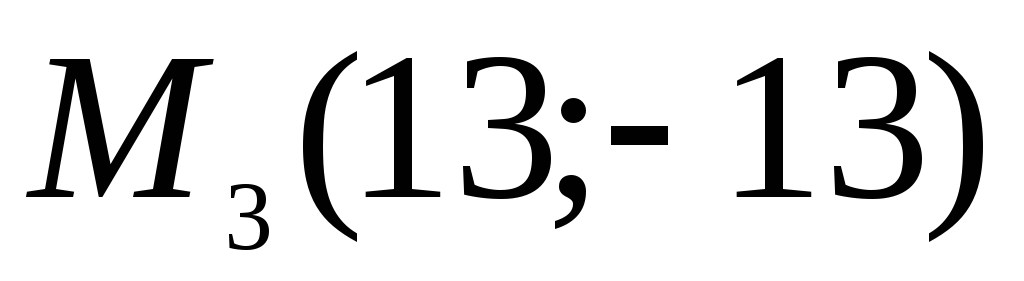определены в новой системе. Вычислить
координаты этих точек в старой системе
координат. -
Составить уравнения прямых, параллельных прямой
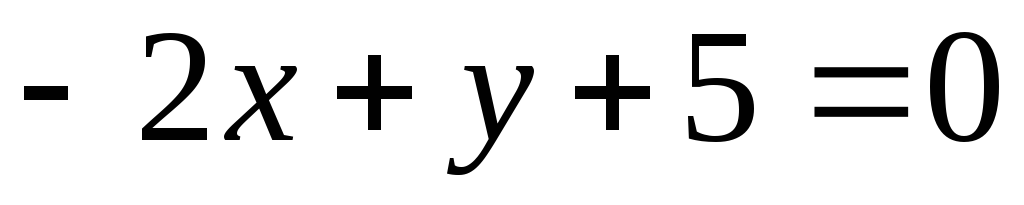и отстоящих от точки А(1;-2) на расстоянии
. -
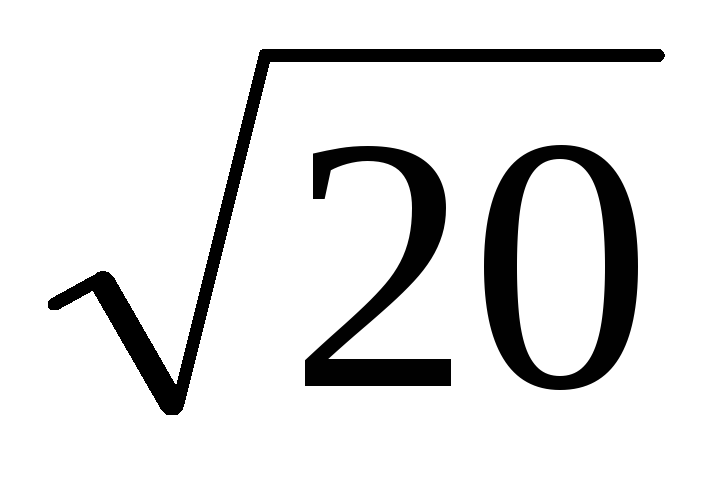Даны последовательные вершины выпуклого четырехугольника А(-3;1), В(3;9), С(7;6), D(-2;-6). Определить точку пересечения его диагоналей.
-
Даны вершины треугольника А(1;-2), В(5;4), С(-2;0). Составить уравнения биссектрис его внутреннего и внешнего углов при вершине А.
-
В параллелограмме
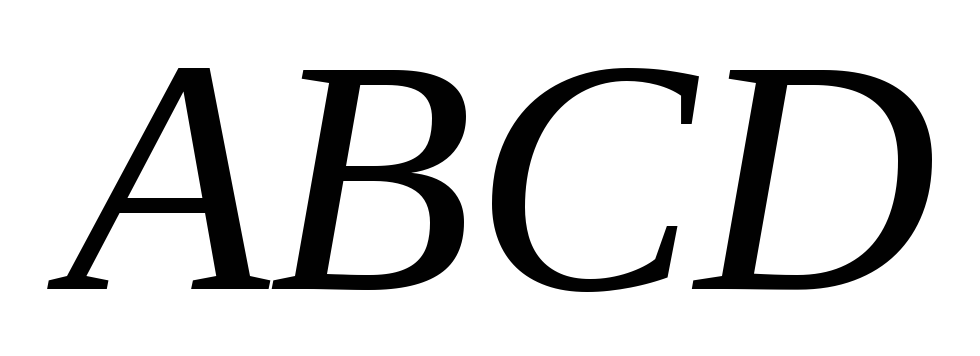точка
лежит на диагонали
,
причем
.
Найти координаты точки плоскости в
системе координат
,
,
,
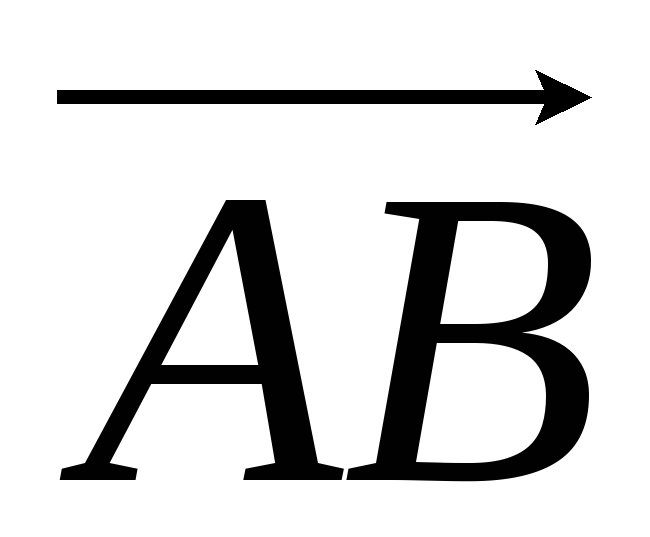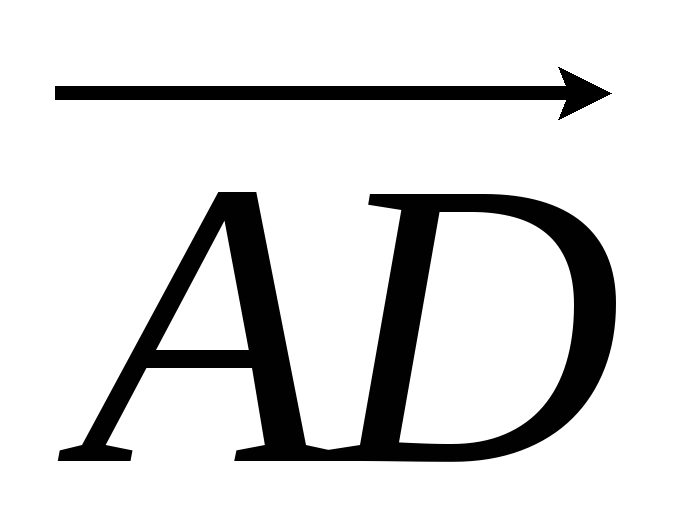если известны ее координаты
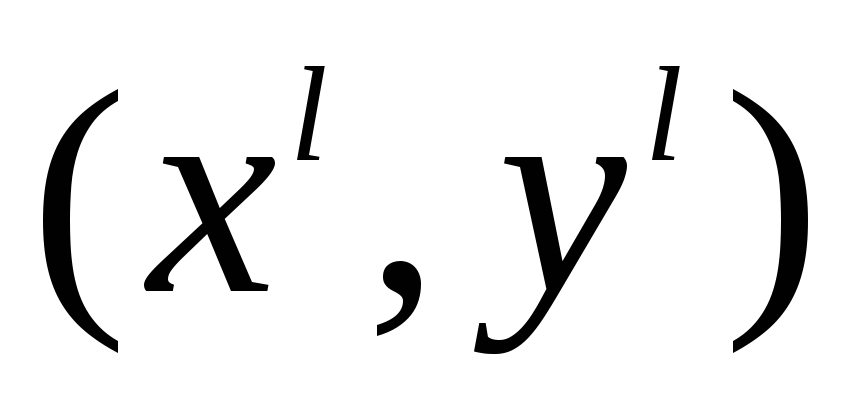в системе координат
,
,
.
Вопросы для самостоятельного изучения
-
Вывод уравнения прямой, проходящей через две данные точки.
-
Вывод нормального уравнения прямой линии на плоскости.