F530EFB30609B81FDFDE985C2ED2DB0F

Глава 2. Системы счисления. Представление информации в ЭВМ

1101011,001110112→X8.

Следовательно, 1101011,001110112=153,1668.

2.3. Количественные характеристики информации

Информацию можно измерить количественно, подсчитать. Существует ряд подходов к измерению информации и свои меры измерения информации (синтаксическая, семантическая, прагматическая).

Синтаксическая мера информации служит для определения количества информации в сообщении и ее объема.

Количество информации измеряют с точки зрения энтропийного подхода, согласно которому факт получения информации всегда связан с уменьшением неопределенности (энтропии) системы. С точки зрения теории информации, предложенной Клодом Шенноном в 1948 г., каждому сигналу соответствует вероятность его появления. Чем меньше вероятность появления того или иного сигнала, тем больше информации он несет. Количество информации можно измерить формулой:

I = − åN pi log2 pi ,

i= 1

где I - количество информации; pi - вероятность появления i-го сигнала; N - количество возможных сигналов.

Информационный объём сообщения измеряется в битах.

Бит (от англ. ВIT – BInary digiT – один двоичный разряд) — это минимальная единица измерения информации, принимающая одно из двух значений: 0 или 1, и равная количеству информации, содержащемуся в сообщении, уменьшающем

неопределенность (энтропию) в два раза.

Бит можно представить как выбор ответа «да» или «нет» на поставленный вопрос. Бросаем монету. При этом с равной вероятностью может выпасть «орел» либо «решка». Перед броском существует неопределенность наших знаний (возможны два события). После броска неопределенность наших знаний уменьшается в два раза, т.к. до броска мы имели два вероятностных события, а после – только одно – т.е. в два раза меньше.

Электронным представлением бита в электронной вычислительной машине является ситуация «есть сигнал/нет сигнала». В матема-

21

Раздел 1. Базовые понятия информатики

тических науках и информатике обычно «да» обозначается цифрой 1, «нет» — цифрой 0.

Основной единицей измерения информации в вычислительных системах является байт.

Байт — это единица измерения информации, кодирующая один символ, представленный на клавиатуре компьютера, и равная восьми бит.

Чем определен тот факт, что байт равен восьми бит? На клавиатуре компьютера представлено, по меньшей мере, 150 стандартных символов (больших и маленьких русских и латинских букв, цифр, знаков препинания, знаков арифметических операций и т.п.). Каждый из этих символов имеет свой, уникальный набор двоичных символов.

При использовании двух разрядов для кодирования символов можно записать только четыре кода: 00, 01, 10, 11. Чтобы увеличить количество возможных комбинаций, нужно добавлять разряды. Для оценки количества возможных комбинаций при использовании определенного числа разрядов используют формулу:

N = 2n ,

где N – количество возможных комбинаций, n – количество используемых при кодировании разрядов.

При n=2, мы имеем четыре комбинации (N=4), что меньше 150. При n=7, N=27=128, что меньше 150.

При n=8, N=28=256. Этого вполне хватает для того, чтобы закодировать 150 символов.

Байт является основой производных единиц измерения информации:

∙1 килобайт=210 байт = 1024 байт; ∙1 мегабайт=210 килобайт=1024 килобайт=220 байт;

∙1 гигабайт=210 мегабайт=1024 мегабайт=230 байт; ∙1 терабайт=210 гигабайт=1024 гигабайт=240 байт; ∙1 петабайт=210 терабайт=1024 терабайт=250 байт.

Семантическая мера информации используется для измерения смыслового содержания информации. Наибольшее распространение здесь получила тезаурусная мера.

22

Глава 2. Системы счисления. Представление информации в ЭВМ

Тезаурус — это совокупность сведений, имеющихся в расположении пользователя или системы и определяющих их способность принимать

поступившее сообщение.

Для понимания и использования полученной информации получатель должен обладать определенным запасом знаний. По мере роста знаний об объекте увеличивается и количество информации, извлекаемой из сообщения.

Прагматическая мера информации определяет ее полезность (ценность) для достижения пользователем поставленной цели.

2.4. Представление числовой информации в ЭВМ

Для представления информации в памяти ЭВМ (как числовой, так и не числовой) используется двоичный способ кодирования.

Элементарная ячейка памяти ЭВМ имеет длину 8 бит (1 байт). Каждый байт имеет свой номер (его называют адресом). Наибольшую последовательность бит, которую ЭВМ может обрабатывать как единое целое, называют машинным словом (рис. 1). Длина машинного слова зависит от разрядности процессора и может быть равной 16, 32 битам и т.д.

Рис. 1. Бит, байт, слово

В ЭВМ применяются две формы представления двоичных чисел: ∙естественная форма, или форма с фиксированной запятой (точ-

кой); ∙нормальная форма, или форма с плавающей запятой (точкой).

В форме с фиксированной точкой каждому разряду ячейки памяти соответствует один и тот же разряд числа, а точка находится справа после младшего разряда, то есть вне разрядной сетки.

Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 битов). Максимальное число при этом соответствует восьми единицам (25510), минимальное – восьми нулям (0). Т.о., диапазон изменения целых неотрицательных чисел: от 0 до 255.

Для хранения целых чисел со знаком отводится две ячейки памяти (16 бит=2 байта). При этом старший (левый) разряд отводится под

23

Раздел 1. Базовые понятия информатики

знак числа (если число положительное, то в знаковый разряд записывается 0, если отрицательное – 1).

Достоинствами представления чисел в формате с фиксированной точкой являются простота и наглядность представления чисел, а также простота алгоритмов реализации арифметических операций.

Недостатком представления чисел в формате с фиксированной точкой является небольшой диапазон представления величин, недостаточный для решения математических, физических, экономических и других задач, в которых используются как очень малые, так и очень большие числа.

Большинство чисел представляются в компьютере в форме с плавающей запятой. В этом случае положение запятой в записи числа может изменяться. С плавающей точкой каждое число изображается в виде двух групп цифр. Первая группа цифр называется мантиссой, вторая – порядком.

Число А может быть представлено в виде:

A = ± m * q± n ,

где m — мантисса числа; q — основание системы счисления; n — порядок числа.

Для единообразия представления чисел с плавающей запятой используется нормализованная форма, при которой мантисса отвечает условию:

1q ≤ m < 1.

Это означает, что мантисса должна быть правильной дробью и иметь после запятой цифру, отличную от нуля.

Преобразуем десятичное число 5,13, записанное в естественной форме, в форму с нормализованной мантиссой:

5,13 = 0,513*102, или 5,13 = 0,513Е+02,

где 0,513 – нормализованная мантисса, Е – десять в степени, 02 – порядок.

Число в формате с плавающей запятой занимает в памяти компьютера 4 (число обычной точности) или 8 байтов (число двойной точности). При записи числа с плавающей запятой выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.

2.5. Представление символьной информации в ЭВМ

Символьная (алфавитно-цифровая) информация хранится и обрабатывается в ЭВМ в форме цифрового кода, т. е. каждому символу

24

Глава 2. Системы счисления. Представление информации в ЭВМ

ставится в соответствие отдельное бинарное слово-код. Необходимый набор символов, предусмотренный в конкретной ЭВМ, обычно включает в себя:

∙буквенно-цифровые знаки алфавита (алфавитов); ∙специальные знаки (пробел, скобки, знаки препинания и др.); ∙знаки операций;

∙управляющие символы, соответствующие определенным функциям.

Среди наборов символов наибольшее распространение получили знаки кода ASCII (ASCII — American Standard Code for Information Interchange) – американский стандартный код обмена информацией – это семиразрядный код, обеспечивающий 128 различных битовых комбинаций. В компьютерах используется восьмиразрядная модификация этого кода.

Вкомпьютерных сетях на территории России используют КОИ-8 (код обмена информацией восьмизначный).

Впоследнее время большое распространение получила универсальная система кодирования текстовых данных – UNICODE. В данной системе символы кодируются 16-разрядными числами. Шестнадцать разрядов позволяют обеспечить уникальные коды для 65536 различных символов – этого достаточно для размещения в одной таблице всех широкоупотребляемых языков.

2.6. Представление графической информации в ЭВМ

Наиболее распространенные из существующих методов представления графических изображений можно разделить на две большие категории: растровые методы и векторные методы.

Общепринятым на сегодняшний день считается представление черно-белых иллюстраций в виде комбинации точек с 256 градациями серого цвета, и, таким образом, для кодирования яркости любой точки обычно достаточно восьмиразрядного двоичного числа.

Для кодирования цветных графических изображений применяется принцип декомпозиции произвольного цвета на основные составляющие.

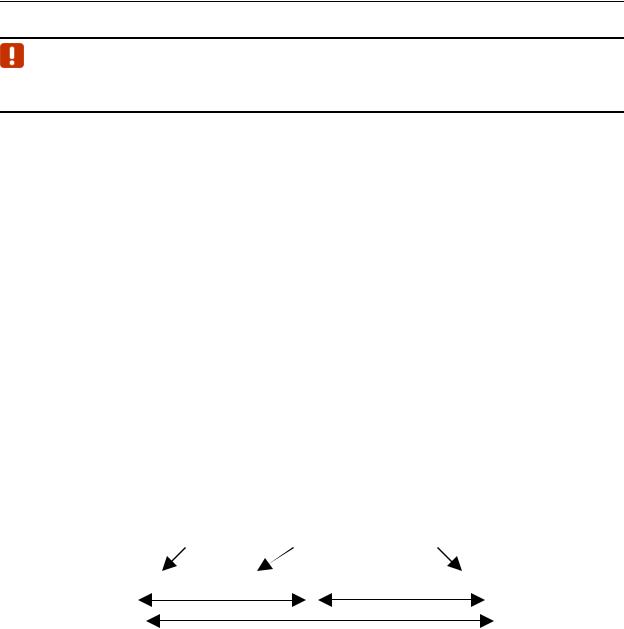
Мы видим предметы потому, что они излучают (например, Солнце, лампочка, монитор) или отражают свет (например, бумага) (рис. 2).

25

Раздел 1. Базовые понятия информатики

Рис. 2. Пути восприятия предметов глазом человека

Так как цвет может получиться в процессе излучения и в процессе отражения, то существуют два противоположных метода его описания: системы аддитивных (от англ. addition – присоединять) и субтрактивных (от англ. subtract – вычитать) цветов.

Цветовая модель RGB – это аддитивная цветовая модель, используемая в компьютерных мониторах, описывающая воспроизведение любого цвета путем сложения трех основных цветов: красного (red, R), зеленого (green, G) и синего (blue,

В).

Если интенсивность каждого из трех цветов достигает 100 %, то получается белый цвет. Отсутствие всех трёх цветов даёт чёрный цвет.

Так как бумага не излучает свет, цветовая модель RGB не может быть использована для создания изображения на печатаемой странице. Поэтому для печати графических изображений используется система цветов, работающая с отраженным светом — система субтрактивных цветов.

Цветовая модель CMYK – это субтрактивная цветовая модель, используемая в полиграфии, описывающая воспроизведение любого цвета путем сложения четырех основных цветов: голубого (сyan, C), пурпурного (magenta, M), желтого

(yellow, Y) и черного (black, K).

В этой модели черный цвет используется для повышения контрастности напечатанных изображений. Черный цвет обозначается буквой К потому, что буква В уже занята синим цветом в модели

RGB.

Таким образом, система RGB работает с излучаемым светом, а CMYK — с отражённым. Если необходимо распечатать на принтере изображение, полученное на мониторе, специальная программа выполняет преобразование одной системы цветов в другую.

Если для кодирования яркости каждой из основных составляющих использовать по восемь двоичных разрядов, как это принято для

26

Глава 2. Системы счисления. Представление информации в ЭВМ

полутоновых черно-белых изображений, то на кодирование цвета одной точки в системе RGB надо затратить 24 двоичных разряда, а в системе CMYK – 32 разряда.

Режим True Color (от англ. true – подлинный, color – цвет) – это режим представления цветной графики с использованием 24 двоичных разрядов в

системе RGB и 32 разрядов в системе CMYK.

Если уменьшить количество двоичных разрядов, используемых для кодирования цвета каждой точки, то можно сократить объем данных, но при этом диапазон кодируемых цветов заметно сокращается.

Режим High Color (от англ. high – высокий) – это режим представления цветной графики с использованием 16 двоичных разрядов.

Вопросы для самопроверки

1.Что такое система счисления?

2.В чем отличие позиционных систем счисления от непозиционных?

3.Как читается число LIV?

4.Какая характеристика системы счисления определяет ее основание?

5.Что такое позиция цифры в числе?

6.Почему двоичная система счисления наиболее удобна для представления информации в ЭВМ?

7.Какое целое десятичное число соответствует двоичному числу 102?

8.Какое целое десятичное число соответствует двоичному числу 1012?

9.Какой цифрой заканчивается четное и нечетное двоичное число?

10.Какие меры информации существуют и в чем их суть? 11.Что определяет термин «бит»?

12.С чем связан тот факт, что 1 байт содержит 8 бит информации? 13.Сколько байт содержит 1 килобайт информации?

14.Что такое тезаурус?

15.Что такое машинное слово?

16.В чем разница между естественной и нормальной формой представления чисел в ЭВМ?

17.Какая формула описывает представление числа в форме с плавающей точкой?

18.Каким условиям должна удовлетворять мантисса при использовании нормализованной формы представления чисел?

19.Сколько битовых комбинаций обеспечивает код КОИ-8?

20.Как кодируется графическая информация, если изображение черно-белое? 21.Чем отличаются системы RGB и CMYK?

22.Что такое режим True Color?

27

ГЛАВА 3

ЛОГИЧЕСКИЕ ОСНОВЫ УСТРОЙСТВ ЭВМ

В главе даются основные понятия алгебры логики: понятие, высказывание, умозаключение. Рассматриваются логические функции и основные законы алгебры логики. Уделяется внимание логическим схемам основных устройств ЭВМ.

3.1. Основы алгебры логики

Основу любого дискретного вычислительного устройства составляют элементарные логические схемы. Работа этих схем основана на законах и правилах алгебры логики, которая оперирует двумя понятиями: истинности и ложности высказывания.

Логика (от греч. logos - слово, мысль, речь, разум) – наука о законах и формах мышления.

Основными формами мышления являются понятие, высказывание и умозаключение.

Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта, которые отличают его от других объектов.

Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о свойствах предметов и отношениях между ними.

В естественном языке высказывания образуются повествовательным предложением или риторическим вопросом. Вопросительные и повелительные предложения не образуют высказывания. Высказывание не содержит внутреннего противоречия и несет смысловую нагрузку.

Высказывание может быть истинным или ложным. На вопрос об истинности простых высказываний отвечают конкретные науки, повседневная практика или наблюдение. Истинность или ложность сложных высказываний (высказываний, состоящих из простых) определяет алгебра логики.

28

Глава 3. Логические основы устройств ЭВМ

Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение

(заключение).

Алгебра логики – наука, с помощью математических методов исследующая операции с высказываниями (создана в середине XIX в. Джорджем Булем).

3.2.Логические функции

Валгебре логики высказывания обозначаются именами логических переменных.

Логическая переменная – это такая переменная, которая может принимать одно из двух возможных значений 0 (ложь, false) и 1 (истина, true).

Для записи операций используют логические функции.

Логическая функция – это логическое выражение, состоящее из логических переменных, связанных между собой с помощью операций алгебры логики.

Логическая функция может принимать два значения: 0 или 1. Логические функции характеризуются таблицами истинности.

Таблица истинности устанавливает соответствие между возможными наборами значений логических переменных и значениями функции.

Основными, или базовыми, функциями алгебры логики служат: ∙конъюнкция (логическое умножение), ∙дизъюнкция (логическое сложение), ∙инверсия (логическое отрицание).

Конъюкция (от лат. conjunctio — соединение) – это логическая функция от двух переменных, которая принимает значение 1 тогда и только тогда, когда

единичное значение имеют все переменные.

Функция может обозначаться: А и В, А and В; A & B; А * В ; А В ;

А В .

29

Дизъюнкция (от лат. disjunctio – разделение) – это логическая функция от двух переменных, которая принимает значение 1 тогда, когда единичное значение

имеет хотя бы одна переменная.

Функция может обозначаться: А или В, А or В; А+В; А В ; А В .

Инверсия – это логическая функция от одной переменной, которая принимает единичное значение при нулевом значении переменной и наоборот.

Функция может обозначаться: А , не А, not А; ¬А.

Таблица 5

Таблица истинности функции инверсии

Импликация (от лат. implico – тесно связаны) – это логическая функция от двух переменных (посылки и следствия), которая принимает значение 0 только тогда,

когда посылка имеет значение 1, следствие – значение 0.

Функция выражается: А → В ; ЕСЛИ А, ТО В; ИЗ А СЛЕДУЕТ В, А ВЛЕЧЕТ В.

30