
3.3. Определенный интеграл.
Основные
определения и теоремы. Пусть на
отрезке[a, b]задана непрерывная функцияy
= f(x)(рис.6.1). Обозначим черезmиMее наименьшее и
наибольшее значения на этом отрезке.
Разобьем отрезок[a,
b]наnпроизвольных частей точками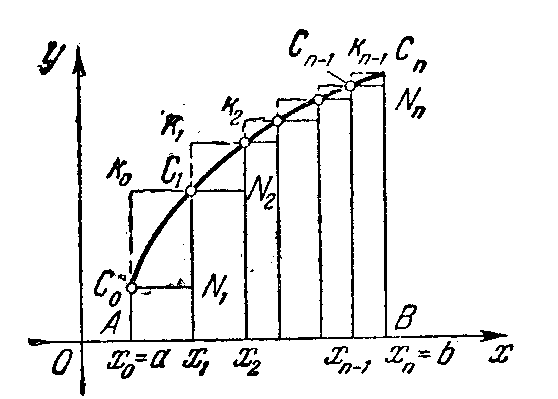
a = x0 < x1 < …< xn–1 < xn = b. Длина каждого из отрезков оставитxi = xi – xi–1. Обозначив наименьшее и наибольшее значения функции на каждом из отрезковmiиMi, составим
Рис. 6.1
суммы
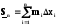 (6.1)
и
(6.1)
и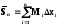 (6.2), называемые нижней и верхнейинтегральнымисуммами.
(6.2), называемые нижней и верхнейинтегральнымисуммами.


Sn(приf (x) 0) численно равна площади вписанной ступенчатой фигурыАС0N1C1N2…Cn–1NnBA,aSn– площади описанной фигурыAK0C1K1…Kn–1CnBA. Так какmi Miдля любогоi, тоSn Sn(знак равенства соответствует случаюf(x) = сonst). Так как m1 m, m2 m, …, mn m (m–наименьшее значениеf(x)на[a, b]), то, Sn m(b–a). Так как M1 M, M2 M,…, Мn M(М– наибольшее значениеf(x) на[a, b]), тоSn M (b – a), т.е. площадь криволинейной трапецииАС0CnВменьше площади описанного и больше площади вписанного прямоугольников.
Возьмем
на каждом из отрезков хiпроизвольную точкуi,
найдем соответствующее значение функцииf(i)и составим сумму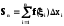 ,
называемую интегральной суммой для
функцииf(x)на отрезке[a,
b]. Очевидно, чтоmi
f(i)
Mi,
mixi
f(i)xi
< MixiиSn
Sn
Sn.
(Фигура, площадь которой равнаSn,
ограничена ломаной, заключенной между
вписанной и описанной ломаными).Snзависит от способа разбиения отрезка[a, b]на отрезки xiи от выбора точекiвнутриxi.
Обозначим черезmaxxiнаибольшую из длин этих отрезков и
потребуем, чтобыmaxxi
0. Число отрезков при этом стремится
к бесконечности.Если при любых
разбиениях отрезка [a, b]
таких, что maxxi
0 и при любом выборе точек i
суммы
,
называемую интегральной суммой для
функцииf(x)на отрезке[a,
b]. Очевидно, чтоmi
f(i)
Mi,
mixi
f(i)xi
< MixiиSn
Sn
Sn.
(Фигура, площадь которой равнаSn,
ограничена ломаной, заключенной между
вписанной и описанной ломаными).Snзависит от способа разбиения отрезка[a, b]на отрезки xiи от выбора точекiвнутриxi.
Обозначим черезmaxxiнаибольшую из длин этих отрезков и
потребуем, чтобыmaxxi
0. Число отрезков при этом стремится
к бесконечности.Если при любых
разбиениях отрезка [a, b]
таких, что maxxi
0 и при любом выборе точек i
суммы
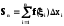 стремятся к одном у и тому же пределу,
то говорят, что функцияf(x)
интегрируема на отрезке [a,
b].Предел этот называют определенным
интегралом от функцииf(x)
на отрезке[a,
b]
стремятся к одном у и тому же пределу,
то говорят, что функцияf(x)
интегрируема на отрезке [a,
b].Предел этот называют определенным
интегралом от функцииf(x)
на отрезке[a,
b]
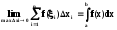 (6.3).
(6.3).
Числа аиbназывают нижним, и верхнимпределамиинтеграла, отрезок[a, b]– отрезком интегрирования,х– переменной интегрирования.
Приведем
теорему существования определенного
интеграла: Еслифункцияf(x)непрерывна на[a, b],то предел
интегральной суммы существует и не
зависит от способа разбиения отрезка[a, b]на элементарные отрезкиxiи от выбора точек i.
Еслиf(x)
0на[a, b],
то определенный интеграл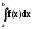 геометрически
представляет собой площадь криволинейной
трапеции, ограниченной линиямиy
= f(x),
х =а, х = b, у = 0.
геометрически
представляет собой площадь криволинейной
трапеции, ограниченной линиямиy
= f(x),
х =а, х = b, у = 0.
Приведем основные свойства определенного интеграла:
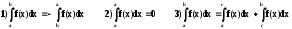
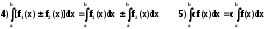 ,
гдес=const.
,
гдес=const.
6). Если m
f(x)
Mна[a, b], то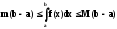
Непосредственное вычисление определенных интегралов как пределов интегральных сумм связано с большими трудностями и требует громоздких вычислений. Рассмотрим метод, упрощающий решение проблемы и использующий связь между интегрированием и дифференцированием.
Формула
Ньютона – Лейбница. Пусть в определенном
интеграле нижний пределафиксирован,
а верхнийbменяется.
Вместе с ним меняется и значение функции,
т.е.интеграл есть функция верхнего
предела. Для работы в привычных
обозначениях верхний предел обозначим
черезх, а чтобы не смешивать его с
переменной интегрирования, обозначим
ее черезtи получим
Ф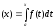 .
Еслиf(t)– неотрицательная функция, то величинаФ(х)численно равна площади
криволинейной трапецииаАХх(рис.6.2.), меняющейся при значениих.
ПроизводнаяФ`(х)похопределится
теоремой:еслиf(x)–непрерывная
функция и Ф
.
Еслиf(t)– неотрицательная функция, то величинаФ(х)численно равна площади
криволинейной трапецииаАХх(рис.6.2.), меняющейся при значениих.
ПроизводнаяФ`(х)похопределится
теоремой:еслиf(x)–непрерывная
функция и Ф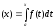 ,то имеет место равенство Ф`(х) =
f(x), т.е. производная от определенного
интеграла по верхнему пределу равна
подинтегральной функции, в которую
вместо переменной интегрирования
подставлено значение верхнего предела.
,то имеет место равенство Ф`(х) =
f(x), т.е. производная от определенного
интеграла по верхнему пределу равна
подинтегральной функции, в которую
вместо переменной интегрирования
подставлено значение верхнего предела.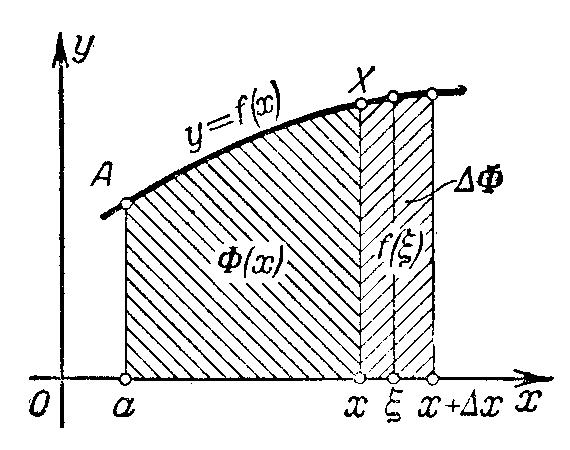
Рис. 6.2
(Из этой теоремы следует, в частности, что всякая непрерывная функция имеет первообразную).
Возможности вычисления определенного интеграла открывает следующая теорема: ЕслиF(x)есть какая – либо первообразная непрерывной функции f(x), то справедлива формула
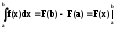 (6.4).
(6.4).
Это
и есть «знаменитая» формула Ньютона –
Лейбница, благодаря которой математика
получила общий метод решения большого
числа различных задач, связанных с
необходимостью вычисления определенного
интеграла. Пример:
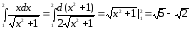
При вычислении определенных интегралов по формуле Ньютона – Лейбница может применяться весь арсенал известных приемов нахождения первообразной, например:
1.
Метод замены переменной:Если дан
интеграл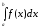 ,где функцияf(x)непрерывна на[a, b]и вводится новая переменная
по формулех = (t),причем ()
= а, ()
= b, (t)и`(t)непрерывны на[,
]
иf[(t)]определена и непрерывна на[, ],то
,где функцияf(x)непрерывна на[a, b]и вводится новая переменная
по формулех = (t),причем ()
= а, ()
= b, (t)и`(t)непрерывны на[,
]
иf[(t)]определена и непрерывна на[, ],то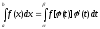 (6.5).
(6.5).
При вычислении
определенного интеграла по формуле
(6.5) мы не возвращаемся к старой переменной,
а находим новые пределы интегрирования
и.
Пример: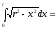 [примем
х =rcost;dx= –rsintdt;
[примем
х =rcost;dx= –rsintdt;
x= 0 приt=/2
и x =rприt= 0] =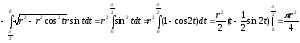
(Геометрически это площадь ¼ круга радиуса r).
2.
Интегрирование по частям.Пустьuиvдифференцируемые
функции отх. Тогдаd(uv)
= udv + vdu.
Интегрируя обе части равенства в пределах
отадоbполучим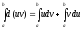 ,
откуда
,
откуда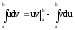 (6.6).
(6.6).
Пример:
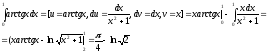
Приведем еще
два соотношения, упрощающие вычисления
в ряде случаев. Если f(x)– нечетная
функция, то (6.7).
(6.7).
и, если f(x)четная функция, то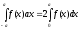 (6.7 ‘).
(6.7 ‘).
Приложения определенного интеграла к задачам практики.
1.
Площадь плоской фигуры. Площадь
криволинейной трапеции, ограниченной
кривойy = f(x),прямымих = аих
= bи отрезком[a,
b], (рис.6.3) вычисляется по формуле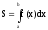 (6.8).
(6.8).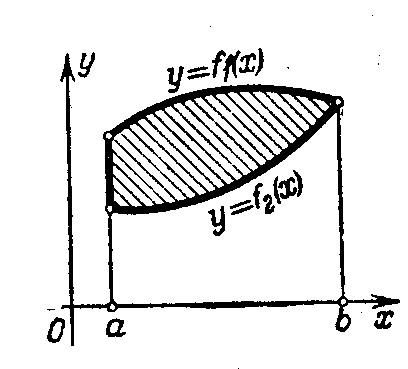
Легко видеть, что площадь фигуры, ограниченной кривыми y = f1(x)иy = f2(x);0 f 2(х) f1(x)и прямымих = а их = b определится соотношением
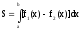 (6.9).
(6.9).
Рис. 6.3
В
полярных координатах площадь криволинейного
сектора, ограниченная кривой
= ()и двумя полярными радиусами
= и
= (
< ) определится
выражением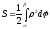 (6.10),
(6.10),
а площадь
фигуры, ограниченной кривыми 1(),
2(),
2()
1()и радиусами
= и
= выражением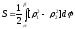 (6.10`).
(6.10`).
2. Длина
дуги плоской кривой. Пусть на плоскости
дана криваяy = f(x). Найдем длину дугиАВэтой кривой между прямымих = аи х = b(рис.6.4.).
Возьмем на дуге точкиА, М1,
…, Мi, …, Вс абсциссамих0 =а, х1,
…xi,
…,xn=
bи проведем хордыА М1, М1М2,
…, Мi–1Mi,
…, Mn–1
B, длины которых
обозначим черезSi.
Получим ломануюАМ1М2
…Мi …В,
вписанную в дугуАВ.Длина ломаной
равна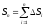 .
ДлинойSдугиАВназывается
предел, к которому стремится длина
вписанной ломаной, когда длина ее
наибольшего звена стремится к нулю:
.
ДлинойSдугиАВназывается
предел, к которому стремится длина
вписанной ломаной, когда длина ее
наибольшего звена стремится к нулю: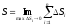 .
.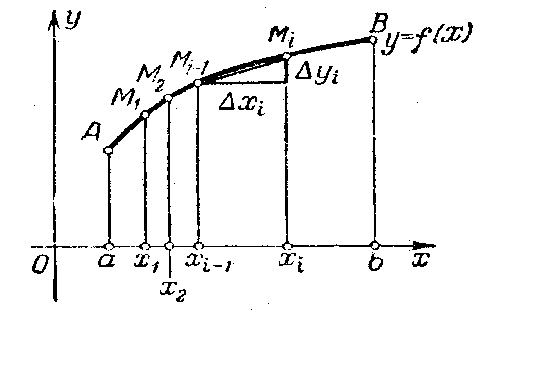
Рис. 6.4
Если
на отрезке [a, b]функцииf(x)иf
`(x)непрерывны (кривая – гладкая), то
этот предел существует и равен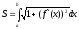 (6.11).
(6.11).
Если
гладкая кривая задана в полярных
координатах уравнением
= ()
(
),
длина дуги равна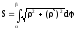 (6.12).
(6.12).
3.
Вычисление объема тела по параллельным
сечениям. Если площадь сечения тела
плоскостью, перпендикулярной осиОх,
может быть выражена как функция отх,
т.е. в видеS = S(x),
то объем части тела, заключенной между
плоскостямих = аиx
= b, определится
формулой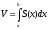 (6.13)
(6.13)
4.
Объем тела вращения. Если криволинейная
трапеция, ограниченная кривойy = f(x) и прямымих = а их = b,
вращается вокруг осиОх, то объем
тела вращения определится соотношением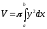 (6.14).
(6.14).
Если вокруг оси Охвращается фигура, образованная кривымиy = f1(x)иy = f2(x)(0 f1(x) f2(x)) и прямымих = а их = b, то объем тела вращения
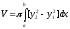 (6.15).
(6.15).
5.
Поверхность тела вращения. Если
дуга гладкой кривойy
= f(x)
( а
х
b)вращается
вокруг осиОх, то площадь поверхности
вращения вычисляется по формуле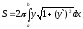 (6.16).
(6.16).
6.
Работа и давление. Работа переменной
силыF = f(x),
действующей по осиОхна отрезке[a, b] вычисляется по формуле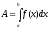 (6.17)
(6.17)
Для
вычисления силы давления жидкости
используют закон Паскаля, согласно
которому давление жидкости на площадку
равно ее площади Sумноженной на глубину погруженияh,
на плотностьи ускорение силы тяжестиgт.е.р = ghS.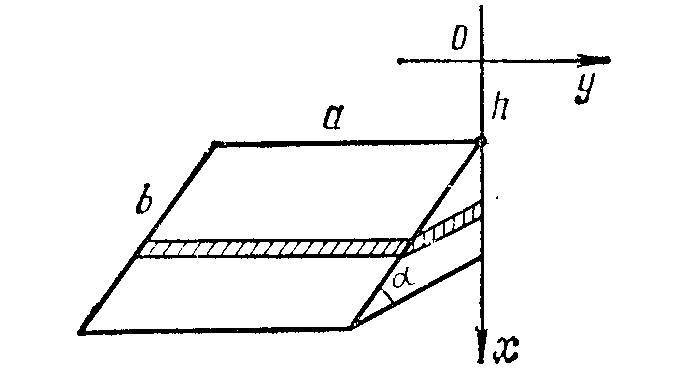
Рис. 6.5
Пример: Какое давление испытывает прямоугольная пластина длиной аи ширинойb (a > b), если она наклонена к поверхности жидкости под угломи ее большая сторона находится на глубинеh(рис.6.5)?
Площадь
выделенной на глубине х элементарной
полоски равна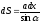 .
Следовательно,
.
Следовательно,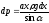 (– плотность
жидкости). Отсюда находим
(– плотность
жидкости). Отсюда находим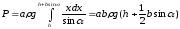 .
.
Несобственные интегралы.
Интеграл
с бесконечными пределами. Рассмотрим
интеграл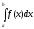 .
При переменномbон
является непрерывной функциейb.
Предел этой функции приb
обозначают
.
При переменномbон
является непрерывной функциейb.
Предел этой функции приb
обозначают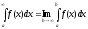 (6.18)
(6.18)
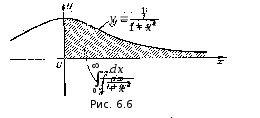
и называют несобственным интеграломот функцииf(x)на интервале[a, ). Если этот предел существует и конечен- интеграл называютсходящимся; если же предел не существует или равен бесконечности –расходящимся.Геометрический смысл в случаеf(x) 0– площадь неограниченной области, заключенной между линиямиy = f(x), х = аи у = 0(осьОх).
Пример:
(рис.6.6)
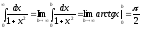 .
.
Аналогично
определяются интегралы:
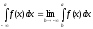 (6.18`)
(6.18`)
и
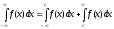 (6.18``).
(6.18``).
Бывает достаточно установить, сходится или расходится данный интеграл и оценить его значение. Это позволяют сделать следующие теоремы:
1.
Если для всех х
а выполняется неравенство о
f(x)
(х)
и если
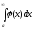 сходится, то сходится и
сходится, то сходится и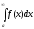 ,
причем
,
причем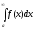
 .
.
2.
Если для всех х
а выполняется неравенство f(x)
(х)
0,
причем
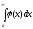 расходится, то расходится и
расходится, то расходится и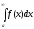 .
.
3.
Если интеграл
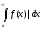 сходится, то сходится и
сходится, то сходится и .
В последнем случае говорят, что интеграл
абсолютно сходящийся.
.
В последнем случае говорят, что интеграл
абсолютно сходящийся.
Пример:
исследовать сходимость
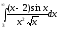 .
Подинтегральная функция знакопеременная.
Рассмотрим
.
Подинтегральная функция знакопеременная.
Рассмотрим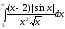 .
Очевидно, что
.
Очевидно, что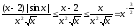 ;
;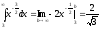 .
Исходный интеграл сходится абсолютно.
.
Исходный интеграл сходится абсолютно.
Интеграл
от неограниченной функции. Пусть
функцияy = f(x)определена и непрерывна
приа х <
с, а в точкесиспытывает бесконечный
разрыв. Интеграл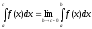 (6.19)
(6.19)
называют несобственным интегралом от неограниченной функции.
Если этот предел существует и конечен – интеграл сходящийся, если нет –расходящийся. Аналогично определяются интегралы
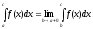 (6.19`)
(6.19`)
(при а < x
cи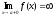 ),
и, если функция имеет бесконечный разрыв
в точкесвнутри отрезка[a, b],
),
и, если функция имеет бесконечный разрыв
в точкесвнутри отрезка[a, b],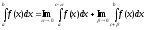 (6.19``).
(6.19``).
Несобственный
интеграл (6.19``) называют сходящимся,
если существуютоба пределав правой
части равенства, ирасходящимся,
если не существует хотя бы один из них.
Для решения вопроса о сходимости
несобственных интегралов от разрывных
функций и оценки их значений полезны
следующие теоремы: 1.Если на отрезке
[a, с] функции f(x)
и (х)
разрывны в точке с, причем
во всех точках этого отрезка (х)
f(x)
0 и
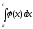 сходится,
то
сходится,
то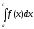 также сходится; 2. Если на отрезке[a,
с] функции f(x) и (х)
разрывны в точке с, причем
во всех точках этого отрезка
f(x)
(х)
0
и
также сходится; 2. Если на отрезке[a,
с] функции f(x) и (х)
разрывны в точке с, причем
во всех точках этого отрезка
f(x)
(х)
0
и
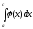 расходится то и
расходится то и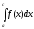 расходится; 3. Если функцияf(x),
знакопеременная на отрезке [a, с],
разрывная только в точке с
и интеграл
расходится; 3. Если функцияf(x),
знакопеременная на отрезке [a, с],
разрывная только в точке с
и интеграл
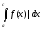 сходится, то сходится (абсолютно) и
сходится, то сходится (абсолютно) и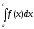 .
.
Пример: Сходится
ли
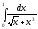 ?
Подинтегральная функция разрывна прих = 0. В указанном интервале
?
Подинтегральная функция разрывна прих = 0. В указанном интервале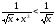 .
Несобственный интеграл
.
Несобственный интеграл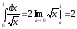
сходится, и, соответственно, сходится исходный интеграл.
Тесты
3.10.
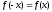 ;
;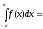
1)
0; 2)
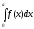 ;
3)
;
3)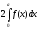 .
.
3.11.
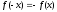 ;
;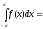
1)
0; 2)
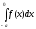 ;
3)
;
3)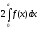 .
.
3.12.
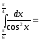
1)
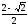 ;
2)
;
2)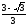 ;
3)
;
3)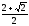 ;
4)
;
4)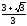 .
.
3.13.
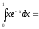
1)
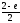 ;
2)
;
2)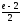 ;
3)
;
3)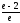 ;
4)
;
4)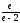 .
.
3.14.
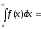
1)
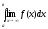 ;
2)
;
2)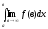 ;
3)
;
3)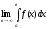 .
.
3.15.
Сходится ли
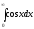 и, если да, то равен:
и, если да, то равен:
1)
0; 2)
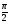 ;
3) 1.
;
3) 1.
3.16.
Сходится ли
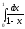 и, если да, то равен:
и, если да, то равен:
1) 0; 2) –3; 3) 2.
3.17.

1)
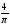 ;
2)
;
2)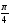 ;
3)
;
3)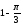 ;
4)
;
4)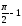 .
.
3.18.
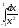
1) Сходится; 2) Расходится.
3.19.
Площадь фигуры, ограниченной линиями
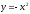 и
и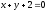 ,
равна (кв.ед):
,
равна (кв.ед):
1) 7; 2) –3,5; 3) 4,5; 4) 6,2.
3.20.
Объем тела, образованного вращением
вокруг оси Ох фигуры, ограниченной
линиями
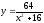 и
и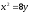 составляет (куб.ед.):
составляет (куб.ед.):
1)
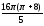 ;
3)
;
3)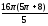 ;
;
2)
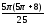 ;4)
;4) .
.
