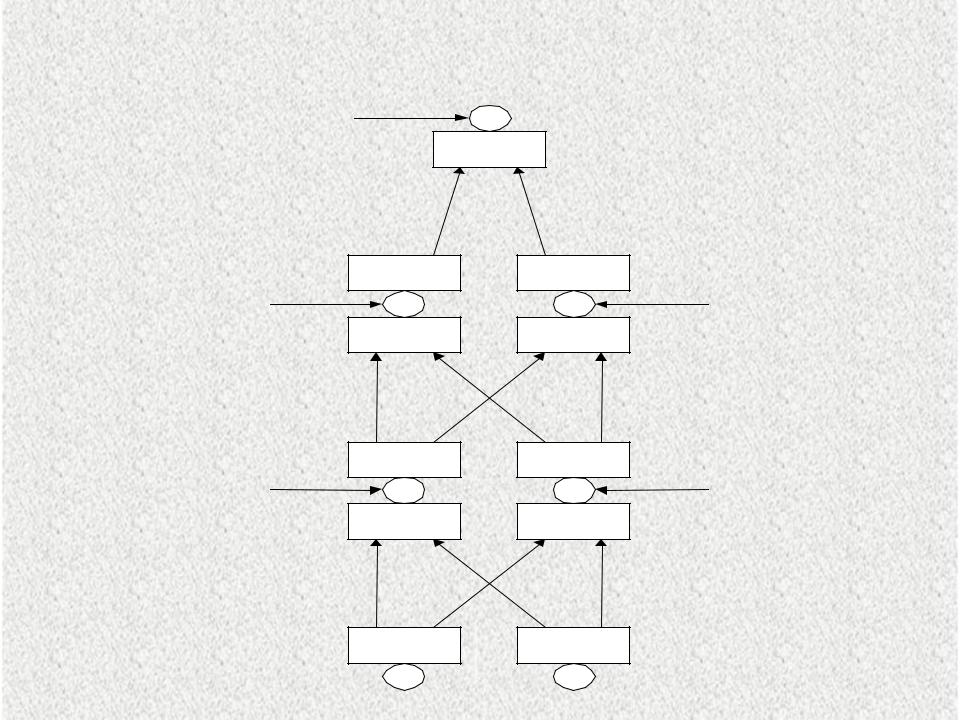
Новые значения весов
-1.0000539
|
7 |
|
-0.00077 |
|
|
1.999958 |
2.999947 |
|
-0.00154 |
-0.00231 |
-2.000001 |
1.9999981 |
6 |
|
5 |
|
|
-0.00027 |
-0.000019 |
|
2.999989 |
|
2.99999999 |
0.99999992 |
1.999986 |
|
-0.00083 |
-0.0006 |
|
0.999986 |
4 |
0.999986 |
3 |
|
|
-0.0002 |
-0.00012 |
|
-1.0000028 |
|
1.9999983 |
1.9999972 |
1.999989 |
|
0.2 |
0.8 |
|
1 |
2 |
|
АЛГОРИТМЫ ОБУЧЕНИЯ НС
Пара- |
Правило |
Архитектура |
Алгоритм |
Решаемая задача |
|
дигма |
обучения |
обучения |
|||
|
|
||||
С |
Коррекция |
Однослойный и |
Алгоритмы |
Классификация |
|
учите- |
ошибки |
многослойный |
обучения |
Распознавание образов |
|
лем |
|
перцептрон |
перцептрона |
Аппроксимация |
|
|
|
|
Обратное |
функций |
|
|
|
|
распространение |
Прогнозирование |
|
|
|
|
Adaline и Madaline |
Управление |
Больцмана |
Рекуррентная |
Алгоритм |
|
|
обучения |
|
|
Больцмана |
Хебба |
Многослойная |
Линейный |
|
прямого |
дискриминантный |
|
распростра- |
анализ |
|
нения |
|
Соревно- |
Соревнование |
Векторное |
вание |
|
квантование |
Сеть ART |
ARTMap |
Классификация Распознавание образов
Анализ данных Классификация Распознавание образов
Категоризация в середине класса Сжатие данных
Классификация Распознавание образов
Парадиг
ма
Без
учителя
Смешан
ная
Правило |
Архитектура |
|
обучения |
||
|
||
Коррекци |
Многослойная |
|
я ошибки |
прямого |
|
|
распространения |
|
Хебба |
прямого |
|
|
распространения |
|
|
или соревнование |
|
|
Сеть Хопфилда |
Соревнов Соревнование ание
SOM Кохонена
Сеть ART
Коррекци Сеть RBF я ошибки
и
соревнова
ние
Алгоритм |
Решаемая задача |
|
обучения |
||
|
||
Проекция |
Категоризация в |
|
Саммона |
середине класса |
|
|
Анализ данных |
|
Анализ главных |
Анализ данных |
|
компонентов |
Сжатие данных |
|
Обучение |
Ассоциативная память |
|
ассоциативной |
|
|
памяти |
|
|
Векторное |
Категоризация |
|
квантование |
Сжатие данных |
|
SOM Кохонена |
Категоризация |
|
|
Анализ данных |
|
ART1, ART2 |
Категоризация |
|
Алгоритм |
Классификация |
|
обучения RBF |
Распознавание образов |
|
|
Аппроксимация |
|
|
функций |
Лекция 3
Нейронные сети Кохонена и Хопфилда
Рассматриваемые вопросы:
1.Алгоритм обучения «без учителя». Решение задачи кластеризации с помощью сетей Кохонена.
2.Рекуррентная сеть Хопфилда. Решение задачи распознавания образов с помощью сети Хопфилда.
X1
X2
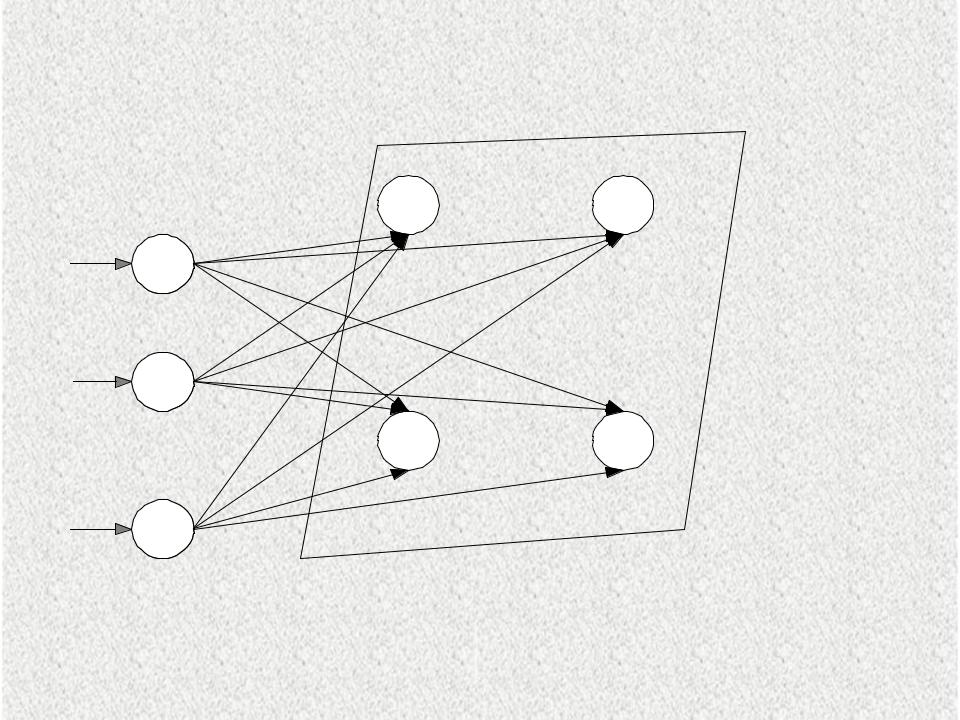
Самоорганизующиеся карты Кохонена (обучение “без учителя”)
...
.. . |
. . . |
|
Функция активации – |
|
гиперболический |
|
тангенс |
X n
. . .
Входной
слой
...
Выходные нейроны карты признаков Кохонена
Рис 3.1.Структура сети Кохонена
|
j |
|
NE(0) |
|
j 1 |
|
NE(t) |
j |
j 2 |
|
|
|
NE(t) |
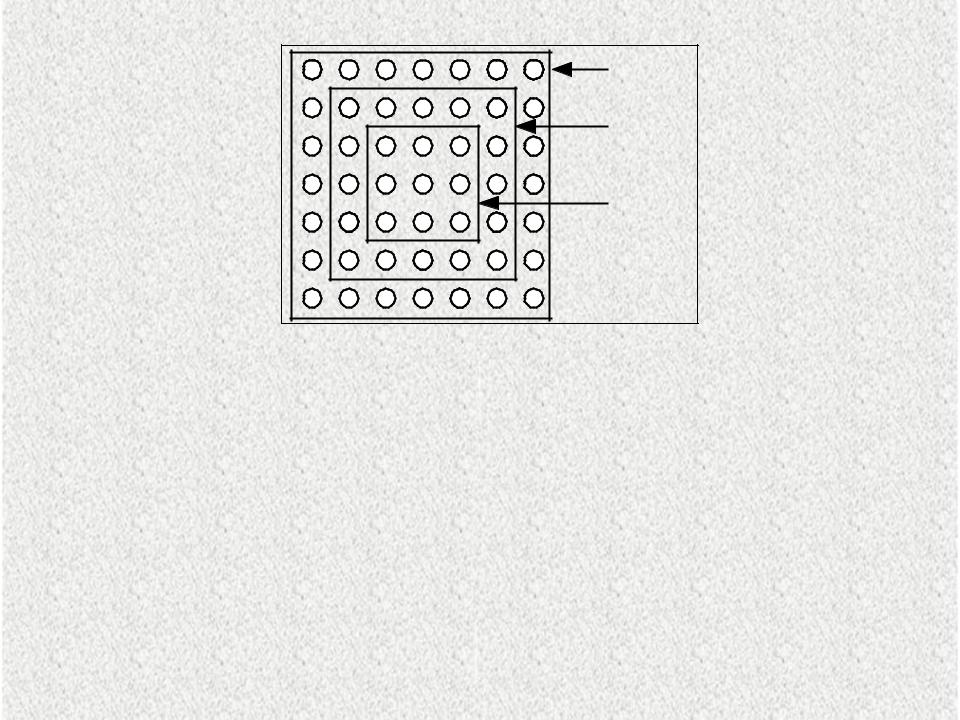
Рис.3.2.Зоны топологического соседства нейронов
NEj(t) множество нейронов, которые являются соседями нейрона j в момент времени t.
Окрестность - это несколько нейронов, окружающих выигравший нейрон.
Алгоритм Кохонена формирования карт признаков:
Шаг 1. Инициализация сети:
Весовым коэффициентам сети присваиваются малые случайные значения. Общее число
синаптических весов - M*N Начальная зона соседства показана на рис.
Шаг 2. Предъявление сети нового входного сигнала.
Шаг 3. Вычисление расстояния до всех нейронов сети: |
|||||||
Расстояния dj от входного сигнала до каждого нейрона j |
|||||||
n 1 |
|
|
|
|
|
|
|
определяется по формуле: |
|
|
|
|
|
|
|
d, j (xi (t) wij (t))2 |
|
|
|
3.1 |
|||
i 0 |
|
|
|
|
|
|
|
Где xi - i-ый элемент входного сигнала в момент времени t, |
|
||||||
wij(t) - вес связи от i-го элемента входного сигнала к |
|
||||||
нейрону j в момент времени t. |
|
|
|
|
|
|
|
Шаг 4. Выбор нейрона с наименьшим расстоянием: |
|
||||||
Выбирается нейрон j*, для которого расстояние dj |
|
||||||
наименьшее. |
XTW |
|
= Σ x w |
|
= z |
|
|
При этом скалярное произведение: |
j |
ij |
j |
3.2 |
|||
|
|
i |
|
||||
Шаг 5. Настройка весов нейрона j* и его соседей:
Производится подстройка весов для нейрона j* и всех нейронов из его зоны соседства NE. Новые значения весов:
wj(t+1) = wj(t) + ŋ(t) µj(t) [x(t) – wj(t)], j=1,m |
3.3 |
где ŋ(t) - шаг обучения, уменьшающийся с течением времени (положительное число, меньше единицы), µ j(t) - функция близости между нейронами слоя Кохонена
Шаг 6. Возвращение к шагу 2 .
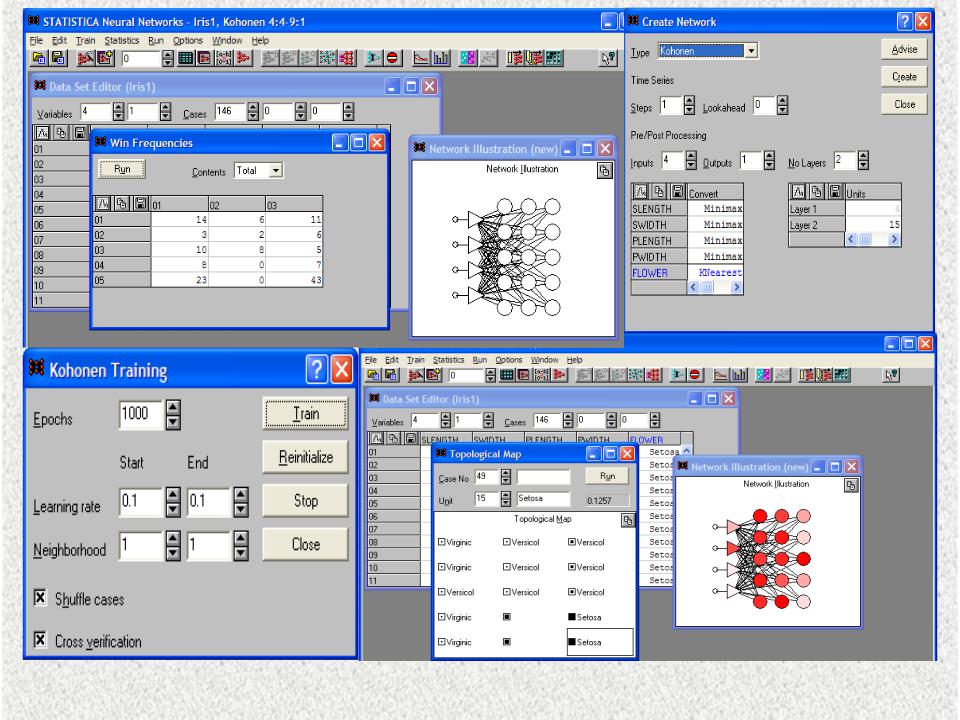
Рис.3.3.Вид основных окон программы Statistica Neurel Networks при моделировании сети Кохонена
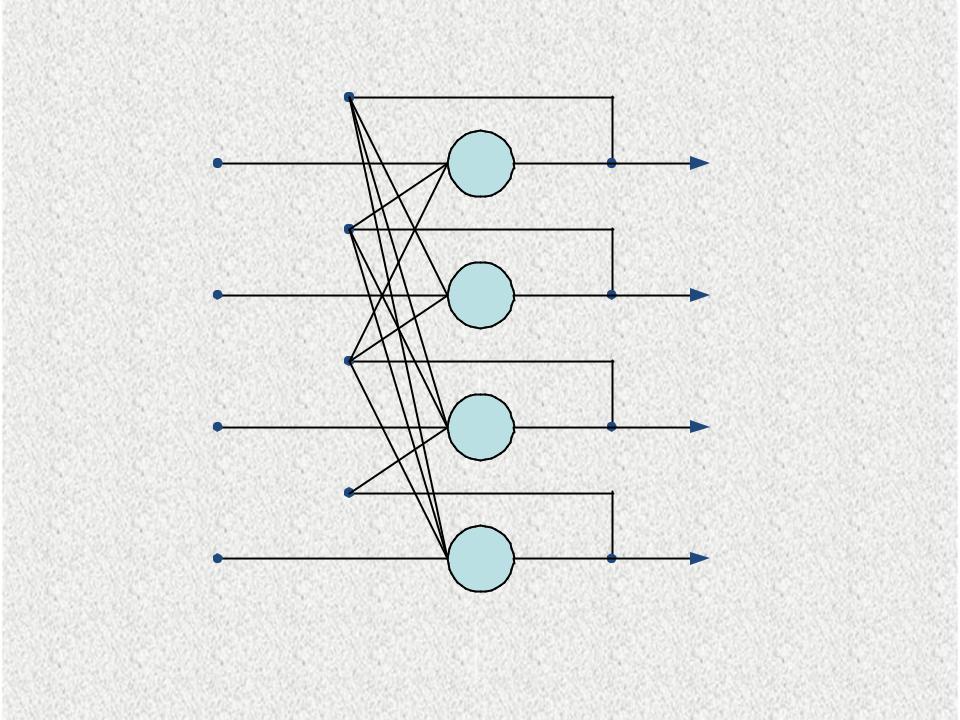
Нейронная сеть Хопфилда
2 |
1 |
Y2 |
|
1 |
|
|
|
X |
2 |
Yi |
|
i |
|||
X |
i |
|
|
n |
... |
Yn |
|
...n |
|||
X |
|
Рис.3.4.Структура нейронной сети Хопфилда